Проверка условия независимости по предпочтению
При проверке условия независимости по предпочтению рассматривают плоскости, где по осям отложены значения двух критериев. Пример такой плоскости для критериев С1 , С2 приведен на рис. 5.2. Сначала предполагается, что по прочим критериям (в нашем случае — по критерию С3) имеются наилучшие значения (Сз = 5 тыс. человек). Первоначально ЛПР должен определить свое предпочтение между альтернативами [(C2)m1in; (C1)max] и [(C2)max; (C1)min]. В нашем случае ЛПР сравнивает площадки для постройки аэропорта с оценками (40 мин., $200 млн) и (90 мин., $100 млн) — две крайние точки А и В на осях, при условии, что С3= 5 тыс. Предположим, что вариант А предпочтительнее. Это означает, что критерий стоимости более важен для ЛПР, чем критерий расстояния. Далее определяется такая точка на шкале критерия С1, что варианты А и К одинаково предпочтительны для ЛПР. Иначе говоря, ищется такая стоимость строительства С*, при которой одинаково предпочтительны варианты (90 мин., $100 млн) и (40 мин., С,*). Затем точно такой же поиск точки безразличия осуществляется при Сз=50 тыс. Если результаты совпадают, то делается вывод, что пара С1,2 С2 не зависит по предпочтению от третьего критерия.
Для полной проверки условия независимости по предпочтениям следует рассмотреть все пары критериев. Однако при приближенной проверке выбираются один или два наиболее существенных критерия и прочие рассматриваются только в паре с ними [7]. При проверке и первого, и второго условий критерии, независимость от которых проверялась, имели крайние значения. Строго говоря, следовало бы рассмотреть и промежуточные значения, но обычно такая проверка считается достаточной. Что делать, если какие-то из условий независимости не выполняются? Теория не дает единственного ответа на этот вопрос. Предлагается определить группу независимых критериев, стоимость функции полезности для подгрупп зависимых и независимых критериев [ и общую функцию полезности «по частям» либо переформулировать задачу. Можно сказать, что нарушение условий независимости существенно усложняет задачу. Поэтому в дальнейшем мы предполагаем, что условия независимости выполняются.
26 Определение весовых коэффициентов (коэффициентов важности) критериев
В MAUT существенно используется понятие весов (коэффициентов важности) критериев. Считается, что ЛПР может найти коэффициенты — числа, которые определяют важность критериев. Отношения между весами критериев устанавливаются поиском точек безразличия на плоскостях двух критериев. В отличие от проверки условий независимости по предпочтению, по осям упорядочиваются значения критериев от худших к лучшим.
На рис. показана плоскость критериев С1, С2 .
Альтернативы А и К находятся в отношении безразличия, которое определяется так же, как и при проверке условия независимости по предпочтению что позволяет записать U($200 млн, 40 мин.) = U($170млн, 90мин.)
В точке равновесия полезности альтернатив равны.
Отметим, что U(40мин.)=1; U(90мин.)=0; U($100млн)=1; U($200млн)=0.
Для аддитивной функции полезности U =∑wiUi.
Тогда U($200 млн) w1 + U(40 мин.) w2 = U($170 млн) w1 + U(90 мин.) w2.
Отсюда w2(U(40 мин.)- U(90 мин.))= w1(U($170 млн)- U($200 млн)).
w2= w1 U($170млн).
| 40 |
| 1 |
| C2 мин |
| C 1 милл $ |
| K |
| A |
| 90 |
| 200 |
| 100 |
| 170 |
Используя полученные ранее однокритериальные функции полезности определяем, что U($170млн)=0,4. Находим w2=0.4 w1 .Аналогичным образом определяется соотношение между весами критериев C1 и С3.
| C 1 милл $ |
| 1 |
| C3 тыс |
| K |
| A |
| 50 |
| 5 |
| 200 |
| 100 |
| 150 |
Пусть U($150млн)= 0,6, тогда w3=w1U($150млн)=0,6w1. Итак, мы выразили веса всех критериев через вес наиболее важного из них и упорядочили критерии по важности. Пусть w1=1, тогда w3=0,6w1=0,6; w2=0.4 w1=0,4.
Вопрос 28. Классические критерии ТПР(0ценочные функции)
Чтобы прийти к однозначному и по возможности наивыгоднейшему варианту решения даже в том случае, когда каким-то вариантам решений αi могут соответствовать различные условия Qj, можно ввести подходящие оценочные (целевые) функции. При этом матрица решений А=\\aij\\ сводится к одному столбцу. Каждому варианту ri приписывается, таким образом, некоторый результат aim характеризующий, в целом, все последствия этого решения. Такой результат мы будем в дальнейшем обозначать тем же символом aim
Возникает, однако, проблема, какой вложить смысл в результат aim
Если, например, последствия каждого из альтернативных решений характеризовать комбинацией из его наибольшего и наименьшего результатов, то можно принять
aim = min aij+ max aij .
Наилучший в этом смысле результат имеет вид
Кк = max aim = max (min aij+ max aij ). (1)
Формируя таким образом желаемый результат, конструктор исходит из компромисса между оптимистическим и пессимистическим подходами.
Рассмотрим теперь некоторые другие оценочные функции, которые в данном примере мог бы выбрать конструктор, а также соответствующие им исходные позиции. Оптимистическая позиция:
Kо= max aim= max (max aij ). (2)
Из матрицы результатов решений (табл.) выбирается вариант (строка), содержащий в качестве возможного следствия наибольший из всех возможных результатов. Наш конструктор становится на точку зрения азартного игрока. Он делает ставку на то, что выпадет наивыгоднейший случай, и исходя из этого выбирает размеры изделия. Позиция нейтралитета:
Kн = max aim= max 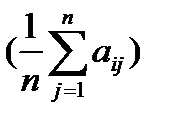 (3)
(3)
i j
Конструктор исходит из того, что все встречающиеся отклонения результата решения от «среднего» случая допустимы, и выбирает размеры, оптимальные с этой точки зрения.








