Вопрос 21.Оценка полезности
Для упрощения дальнейшего изложения разобьем всю процедуру оценки функций полезности на пять этапов:
1) предварительный анализ для фактической оценки;2) определение соответствующих качественных параметров;3) формирование количественных ограничений;4) выбор функции полезности; 5) проверка на согласованность.
3.1. Предварительные процедуры для фактической оценки полезности
Оценка функций полезности, по-видимому, скорее искусство, чем наука. Успех в данной области тесно связан со способностью исследователя вступать в контакт с лицом, принимающим решение. Исследователь должен доказать этому лицу важность таких оценок, заручиться его поддержкой и сделать удобной процедуру оценивания.
3.2. Определение соответствующих качественных параметров
Нас интересуют такие качественные характеристики, как монотонность и отношение лица, принимающего решение, к риску. Достаточно просто можно установить, выполняется ли условие монотонности. Спросим лицо, принимающее решение, что оно больше предпочитает: х1 или x2 (где x2>x1). Вероятно, эксперт ожидал бы ответа на этот вопрос, основываясь на собственной оценке исходов (последствий). Если x2 предпочтительнее, то он склонился бы к мнению, что предпочтения монотонно возрастают на множестве свойств (признаков) X. А затем (чтобы окончательно удостовериться) ему следует спросить, всегда ли большее значение х предпочтительнее меньшего.
Допустим, что предпочтения монотонно возрастают в X, как, например, предполагается в случае прибыли. Тогда будем говорить, что некий субъект уклоняется от риска, если для любых значений х1 и x2 сумма (х1+x2)/2 предпочтительнее лотереи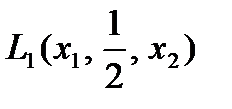 
, которая имеет исходы х1 и x2 с одинаковой вероятностью. Отметим, что величина (х1+x2)/2 представляет собой математическое ожидание лотереи L (в противоположность полезности). Кроме того, будем говорить, что субъект стремится к риску, если он предпочитает лотерею Li по сравнению с величиной (х1+x2)/2 при всех значениях х1 и x2. И наконец, субъект безразличен (нейтрален) к риску, если ему безразлично, что он получит: лотерею L или величину (х1+x2)/2 для любых х1 и x2. Приведенные характеристики отношения к риску удобно использовать для описания областей и функций полезности (рис. 3.1).
Функция полезности вогнута, выпукла или линейна соответственно, если лицо, принимающее решение, уклоняется от риска, стремится к нему или безразлично.
Рис. 3.1 Отношение к риску.
Для выяснения отношения к риску можно разделить область возможных значений Х на четыре равные части с исходами, обозначаемыми через x0, х1, x2, x3 и х4. Затем следует спросить у лица, принимающего решение, что для него предпочтительнее: лотереи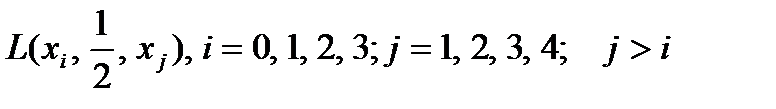 
, или соответствующие математические ожидания данных лотерей 
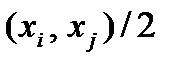. Если все ответы демонстрируют одно и то же отношение к риску, то следует предположить, что такое отношение к риску у данного лица преобладает.
Существуют более тонкие характеристики риска, для описания которых требуется понятие гарантированного эквивалента. Гарантированным эквивалентом лотереи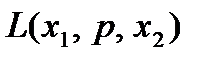 
называется величина 
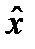, которую лицо, принимающее решение, считает равноценной L. Премия за риск определяется как математическое ожидание выигрыша минус гарантированный эквивалент.
Предположим, что лицо, принимающее решение, уклоняется от риска, а 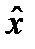и r— гарантированный эквивалент и премия за риск соответственно для лотереи 
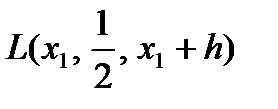, где h — положительная величина. Тогда, очевидно, 
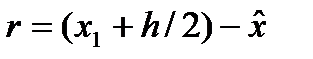. Говорят, что имеет место постоянное уклонение от риска, если премия за риск в лотерее L не зависит от величины x1. В этом случае при возрастании х1 на некоторую величину k гарантированный эквивалент должен увеличиться на ту же величину k. Как показано в работе [59], если наблюдается постоянное уклонение от риска, то функция полезности будет иметь вид
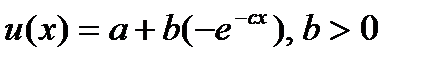, (3.1)
где а и b — произвольный набор скалярных констант.
3.4. Выбор функции полезности
Предположим, что можно найти некоторое параметрическое семейство функций полезности, которые обладают определенными заранее установленными свойствами. Обозначим такое семейство функций полезности через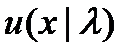 
, где 
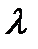— параметры. Тогда выбор соответствующей функции полезности сводится к выбору значений параметров. Используя параметрическую форму записи и предыдущие оценки отдельных частей кривой полезности [например, (2.6)], можно записать уравнение
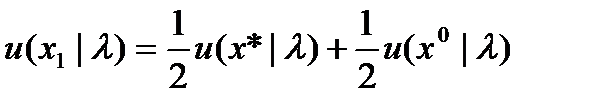, (3.6)
где число неизвестных равно числу параметров. Используя значения гарантированных эквивалентов, полученных экспертным путем, запишем столько уравнений, сколько неизвестных, и разрешим их относительно параметров, чтобы иметь возможность построить функцию полезности, как показано на рис. 3.1.
Для проверки внутренней совместимости смешанного набора качественных и количественных ограничений, налагаемых на функцию полезности, разработан метод, описанный в [52]. 3.5. Проверка на согласованность.
Одна из наиболее общих и существенных ошибок, которые обычно делаются при оценке функций полезности, связана с подбором параметров при использовании очень узких диапазонов изменения гарантированных эквивалентов лотерей. Например, предположим, что лицо, принимающее решение, считает гарантированный эквивалент лотереи L(200, 
,0) равным 80, и пусть функция полезности для стратегии постоянного уклонения от риска определяется, исходя из этого. Экстраполяция гарантированного эквивалента, основанная на результирующей функции полезности, даст значение гарантированного эквивалента для лотереи L(1000, ,0), которое будет много меньше, чем эмпирическая оценка эксперта.