Вопрос 20. Числовая форма представления неопределенности суждений (3 метода).
Рассмотрим некоторое событие Е. У лица, принимающего1 решение, может быть некоторое представление о вероятности р(Е) наступления события Е. Такая вероятность р (Е) определяется пятой аксиомой теории принятия решений. Будем в дальнейшем называть ее субъективной вероятностью. Эта вероятность отражает степень уверенности лица, принимающего решения, в том, что событие Е наступит, и в ее основе лежит готовность данного лица действовать в соответствии с этой уверенностью. Лицо, принимающее решение, может указать свои субъективные вероятности для различных возможных событий на основе многочисленных соображений. Сюда входят знания о физических явлениях, эмпирические данные, результаты моделирования взаимосвязи различных факторов и экспертные суждения многих лиц, главным образом специалистов в рассматриваемой области. Одним из экспертов является лицо, принимающее решение.
1. Вероятность, основанная на физических явлениях
В некоторых ситуациях можно предположить, что все возможные события некоторого эксперимента равновероятны. Поэтому если существует N возможных событий, то вероятность каждого из них равна 1/N. Основываясь на таком предположении, мы обычно приписываем вероятность 1/2 выпадению герба на правильной монете и вероятность 1/6 выпадению шестерки на игральной кости. Вероятности, которые можно проверить исчерпывающими экспериментами, часто называют объективными вероятностями. Большинство людей обычно согласны с такими вероятностями.
Если некоторое лицо принимает их как руководство к действию, объективные вероятности, по определению, являются также и субъективными вероятностями.
2.Вероятность, основанная на имеющихся данных и результатах моделирования
Если имеются данные о возможности наступления интересующих нас событий, то их можно использовать для формирования суждений о вероятностях событий. Пусть El, Е2, . .., Еп — полный набор взаимоисключающих событий. Если в каждом из N испытаний наблюдалось одно из событий: или Е1 или Е2, ..., или Еп, причем Ni раз наблюдалось событие Еi то вероятность Ei равна Ni/N. Например, если среди последних 25 000 звонков о пожаре в городе 10 000 оказались ложными, то субъективно можно положить, что вероятность ложного сигнала о пожаре равна 0,4. Далее будет рассмотрен способ взаимосвязи таких данных с оценками суждений.
В некоторых ситуациях имеющиеся данные можно уточнить и дополнить. Например, можно построить аналитическую или имитационную модель, чтобы выяснить влияние различных параметров на входе на важнейшие переменные на выходе. При помощи такой модели можно получать вероятности появления интересующих нас переменных на выходе, используя данные о вероятностях появления переменных на входе. В аналитических моделях применяется теория получения распределений вероятностей , а при имитационном моделировании — метод Монте-Карло .
3.Определение вероятности одиночного события
Вероятности интересующих нас событий часто трудно получить из-за недостатка статистических данных и сведений. Особенно это касается ситуаций, в которых приходится принимать единственные в своем роде стратегические решения. В таком случае необходимо выработать суждения либо о входных переменных модели, либо о самих представляющих интерес величинах. Чтобы проиллюстрировать это, предположим, что нас интересует событие Е и ему приписана субъективная вероятность р (Е), которая пока не определена.
Рис. 1. Получение числовых значений субъективной вероятности наступления одиночного события.
Сначала построим две лотереи (рис. 1): L1 = (х*, р, х°) и L2, которая имеет исход х*, если осуществилось событие Е, и исход х°, если событие E не произошло. Исход х* выбирается так, что он является более предпочтительным, чем х°. Затем при фиксированном значении р лицу, принимающему решение, задается вопрос: «Какая лотерея более предпочтительна или они равноценны?» Если L1 
L2, то величину р уменьшают и повторяют вопрос. Если L2 L1, то увеличивают р и снова повторяют вопрос. Через несколько итераций найдется такое значение р (обозначим его через р'), при котором L1 равноценна L2 (L1 ~ L2). Тогда субъективная вероятность события Е равна р' (т. е. вероятность события, определенная на основе суждения лица, принимающего решение). Если Ei (i = 1, 2, . . ., п) — полный набор всех взаимоисключающих событий, то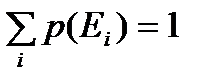 
. Оценки вероятностей, полученные на основе суждений некоторого лица, следует подставить в эту сумму и, если сумма не равна единице, то необходимо изменить рассматриваемые оценки
4. Оценочные суждения о распределении вероятностей
Наиболее общим подходом к оценке распределения вероятностей величин, принимающих бесконечное количество значений, является так называемый дробный метод. Согласно этому методу, берут несколько точек функции распределения рассматриваемой величины и затем «подгоняют» кривую, оптимальным образом проходящую через эти точки.
Предположим, что мы хотим получить распределение вероятностей некоторой величины X; конкретные значения X обозначим через х. Например, X может быть доходом, а х = 100 000 долл. Сначала попытаемся оценить дробь 0,5, т. е. такое значение х05, при котором вероятность события (X < х05) равна 0,5. Лицу, принимающему решение (или назначенному эксперту), задают вопрос: «При каком значении х равновероятно, что величина X будет больше или меньше этого значения?» Ответ на поставленный вопрос можно получить, используя итерационную процедуру, описанную в предыдущем разделе. В результате применения этой процедуры получается значение х05. Затем задают следующий вопрос: «Предполагая, что величина X меньше значения х05, какое значение х разделит интервал [ -∞, х05] на равновероятные
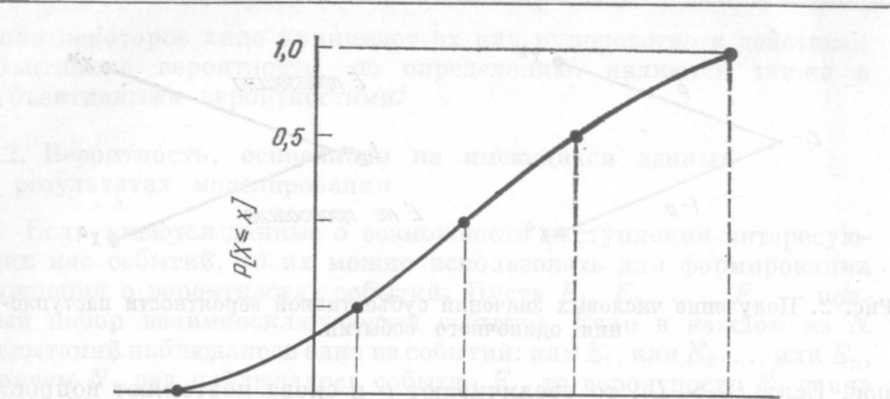
| Х0,01 0 Х 0,25 Х 0,5 Х 0,75 Х 0,99 X Рис. 2. Функция распределения вероятностей величины X. |
части?» Ответ на этот вопрос есть х0,25, т. е. дробь 0,25. Конечно, вероятность (X < х0,25) должна быть равна 0,25. Аналогично получаем значение £0 75. И наконец, попытаемся оценить значения х0,01 и х0,99 задавая, например, вопрос: «Какое значение х Вы бы выбрали, чтобы вероятность того, что величина X меньше этого х, составляла 0,01?» Ответом будет значение х001.
Продолжая такое дробление, можно получить набор величин хк, таких, что вероятность (X < xк) равна к, т. е.
Р(Х<хк)=к. (13)
Точки (xк, к) можно нанести на график, как показано на рис. 2, и гладкая кривая, соединяющая их, будет представлять функцию распределения вероятностей величины X. Продифференцировав эту функцию, получим плотность вероятности.