Предпочтение и безразличие

Дата: 2025-05-01; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

В теории предпочтений используются два основных бинарных отношения на множестве X. Во-первых, отношение нестрогого предпочтения >; запись х > у читается следующим образом: «х либо предпочтительнее, чем у, либо безразличен к у». Чаще пользуются формулировкой: «г/ не предпочтительнее, чем х». Во-вторых, применяется отношение предпочтения ; запись х у читается так: «х предпочтительнее, чем у». Отношение нестрогого предпочтения чаще встречается в литературе, но в последнее время некоторые авторы стали пользоваться последним определением.

Когда в качестве основного бинарного отношения берется отношение нестрогого предпочтения (>;), то отношения предпоч­тения ( ) и безразличия (~) определяются через нестрогое пред­почтение >~ следующим образом:

х у тогда и только тогда, когда х ~ у, и неверно, что у ~ х;
х~ у тогда и только тогда, когда х ~ у и у ~ х. (1)

Если же в качестве основного бинарного отношения берется , то отношение безразличия и отношение нестрогого предпочтения определяются на основе как

х~ у тогда и только тогда, когда неверно х у и неверно у х;
х ~ у тогда и только тогда, когда х у или неверно х у
и неверно у х.

14. Теория полезности (проблема транзитивности, карты безразличия)

Отношение предпочтения на X транзитивно, если из того, что х предпочтительнее, чем у, а у предпочтительнее, чем z, сле­дует, что х предпочтительнее, чем z. В целом это свойство кажется разумным, поэтому будем предполагать, что оно выполняется в большинстве дальнейших рассуждений. Транзитивность нару­шается, если (х > у, у > z, х~ z) или (х у, у z, z х) для некоторых х, у и z из X.

Отношение безразличия (~) на X транзитивно, если из того, что х безразличен по отношению к у, а у безразличен к z, следует, что х безразличен по отношению к z. Отношение безразличия не транзитивно, если существуют х, у и z, для которых х ~ y, у ~ z и х z. Хотя во многих примерах нетранзитивных безраз­личий используется несколько критериев или характерных признаков, можно привести и простейшие «одномерные» примеры, демонстрирующие тот же факт. Для этого можно рассмотреть си­туацию с некоторым пороговым предпочтением, которое остается незамеченным благодаря несущественным или малым различиям в предпочтениях. В работе [38] это рассмотрено на примере чашки кофе, в которую добавляют один за другим маленькие кусочки сахара. Можно ожидать безразличного отношения к х и (х + 1) кусочкам сахара для х, скажем в пределах от 0 до 5000, но трудно ожидать одинакового отношения к двум чашкам кофе, в одной из которых нет сахара, а в другой х = 5000.

Поскольку отноше­ние ~ транзитивно, оно является отношением эквивалентности (транзитивным, симметричным, рефлексивным) и, следовательно, может быть использовано для разделения (разбиения) множества X на классы эквивалентности, или классы безразличия. Такие классы представляют собой непустые множества из X: если А и В — два различных класса и х лежит в А, & у в В, то х~ у тогда и только тогда, когда А =В\ если же х у, то х' у' для любого х' из А и каждого у' из В. На рис. 2 изображены классы безразличия для случая двух продуктов или двух характерных признаков.

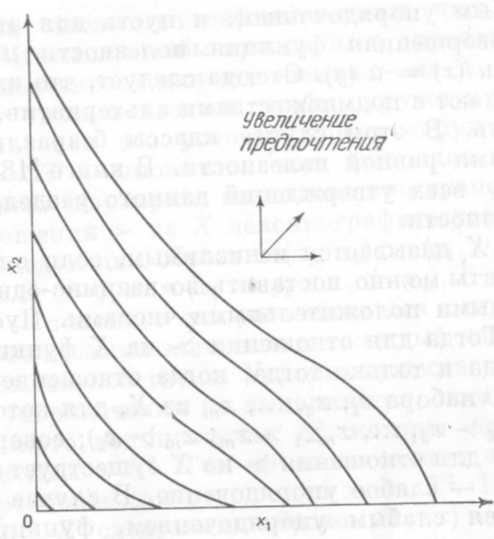
Рис. Карта безразличия.


  1. Полезности и линейная функция полезности (линейная комбинация распределений)

Пусть и — вещественная функция, определенная на X. Функция и называется функцией полезности для отношения предпочтения на X, если и(х) > и(у) для любых x и y, таких, что х y; и называется совершенной функцией полезности для отношения на X, если для всех х и у из Х справедливо неравенство и(х) > и(у) тогда и только тогда, когда х у. Пусть отношение на Х может существовать, если только отношение является слабым упорядочением, и пусть для этого отношения определена совершенная функция полезности u; тогда 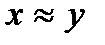, если и только и(х)=и(у). Отсюда следует, что классы безразличия в Х совпадают с подмножествами альтернатив, имеющих равную полезность.

Теория принятия решений использует различные процедуры, позволяющие формализовать предпочтение, т.е. выразить их в единой количественной мере. Основой для таких процедур является теория полезности, разработанная Дж. Фон Нейманом и О. Моргенштерном [33]. Ее математическая основа – система аксиом, в которых утверждается, что существует некоторая мера ценности, позволяющая упорядочить результаты решения. Эта мера называется функция полезности решений или полезностью.

Простым распределением вероятностей р называется вещественная функция Р, которая принимает положительные значения на большинстве элементов х из конечного множества X, а сумма всех значений р(х) равна единице. Мы не будем рассматривать непростые распределения. В зависимости от контекста распределения из Р часто называют ставками, играми, лотереями, альтернативами риска, смешанными стратегиями и рандомизированными стратегиями. Для любых распределений р и q из Р выражение 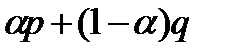называется прямой линейной комбинацией распределений р и q; здесь a — действительное число, заключенное между 0 и 1. Таким образом, если 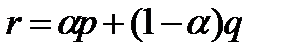, то 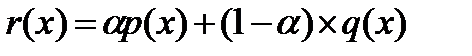для любого x из X. Если р и q принадлежат Р и 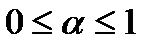, то 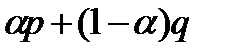также принадлежит Р.

Предположим, что элементами Х являются некоторые суммы денег и пусть р(0 долл.)=0,3; р (10 долл.)=0,2; р (20 долл.)=0,5; q (7 долл.)=0,7; q (10 долл.)=0,3 и 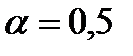. Тогда 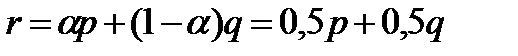;r(0 долл.)=0,15; r(7долл.)=0,35; r(10 долл.)=0,25 и r(20 долл.)=0,25.