3. Генерация возможных решений т.е. формирование списка альтернатив.
4. Оценка возможных альтернатив, исходя из предпочтений ЛПР и ограничений, накладываемых внешней средой.
5. Анализ последствий принимаемых решений.
6. Выбор лучшего, с точки зрения ЛПР, варианта.
11. Шкалирование (шкалы)
Для оценки критерия используются различные шкалы.
Числовые: порядковые, равных интервалов, пропорциональных оценок.
Лингвистические.
Любое положительное линейное преобразование л следующего вида:
и (х) = а + b л (х), b> 0, (1)
будем называть шкалой полезности для исходов х. Если лицо, принимающее решение, опирается на данные аксиомы, ему надлежит всегда выбирать альтернативы так, чтобы максимизировать ожидаемую полезность. Согласно сформулированным аксиомам, не существует других процедур принятия решений.
Поскольку максимизация ожидаемой полезности эквивалентна максимизации ожидаемого значения л в (1), произвольный выбор» х* и х° не влияет на фактическое решение. Шкала полезности аналогична температурным шкалам; разные шкалы, которые получаются одна из другой с помощью положительного линейного* преобразования, эквивалентны с позиции их использования для целей принятия решений.
12. Теория полезности (основные положение, принципы)
Термин «полезность» имеет два разных значения. Первое (более важное) — это качественная, или сравнительная, оценка, характеризуемая такими утверждениями, как: «Я ценю это больше, чем то» или «Я предпочитаю х, а не у». Второе значение этого термина — количественная оценка, когда мы в виде числа выражаем наше предпочтение, пытаясь отразить его сравнительную природу. . Учитывая такую двойственность, мы будем использовать термин «предпочтение» для отображения качественной характеристики объекта, а термин «полезность»— для количественного представления предпочтений.
Под системой предпочтения ЛПР понимается совокупность его представлений о преимуществах и недостатках сравниваемых решений.
Решающее правило r (метод принятия решения) отражает информированность ЛПР о возможных исходах выбранных решений, а также предпочтительность тех или иных исходов. Решающее правило может быть задано в виде аналитического выражения, алгоритма или словесной формулировки.
13. Теория полезности (бинарные отношения, предпочтение и безразличие)
Фундаментальным понятием теории предпочтений является бинарное отношение, поэтому необходимо изложить некоторые положения теории бинарных отношений.
Бинарное отношения R на непустом множестве X есть подмножество множества всех упорядоченных пар элементов из X; множество всех упорядоченных пар задается прямым произведением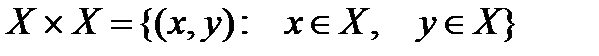 
. Запись xRy (читается: x находится в отношении R к y) означает, что (x,y) принадлежит R; аналогично не xRy (записывается как 
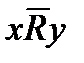) означает, что (x,y) не принадлежит R, или что x не находится в отношении R к y.
Ниже указаны восемь возможных свойств бинарных отношений, разделенных на четыре группы. Во всех определениях предполагается, что х, у и z являются элементами множества X. Бинарное отношение R на множестве Х является:
1) рефлексивным, если xRx для каждого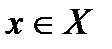 
; нерефлексивным, если 
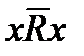для каждого 
;
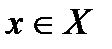2) симметричным, если из xRy следует yRx; асимметричным, если из xRy следует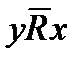 
;
3) транзитивным, если из xRy и yRz следует xRz; отрицательно транзитивным, если из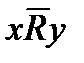 
и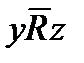 
следует 
;
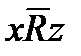4) связным, если xRy или yRx; слабосвязным, если из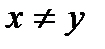 
следует xRy или yRx.
Пусть X — множество всех живых людей. Тогда отношение «выше, чем» является нерефлексивным, асимметричным, транзитивным и отрицательно транзитивным; отношение «ему (ей) столько же лет, как и» рефлексивно, транзитивно, отрицательно транзитивно и связно; отношение «является сестрой» (по крайней мере один из родителей общий) симметрично (но почему не транзитивно?); отношение «знаю имя», используемое при исследованиях пациентов с потерей памяти, не удовлетворяет ни одному из перечисленных свойств.