Независимым контуром ЭЦ называется такой контур, который отличается от других хотя бы одной новой ветвью, входящей в него.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
1. Законы Кирхгофа и их применение в расчетах электрических цепей.
Первый закон Кирхгофа. Алгебраическая сумма токов, сходящихся в узле электрической цепи, равна нулю.
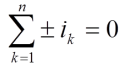
Суммирование распространяется на токи в ветвях, сходящихся в рассматриваемом узле.
Первый закон Кирхгофа выражает тот факт, что в узле электрический заряд не накапливается и не расходуется. Сумма электрических зарядов, приходящих к узлу, равна сумме зарядов, уходящих от узла за один и тот же промежуток времени.
Первый закон Кирхгофа применим не только к узлу, но и к любому контуру или замкнутой поверхности, охватывающей часть электрической цепи, т.к. ни в каком элементе цепи, ни в каком режиме электричество одного знака не может накапливаться.
Второй закон Кирхгофа. Алгебраическая сумма ЭДС в любом замкнутом контуре цепи равна алгебраической сумме падений напряжения на элементах этого контура.
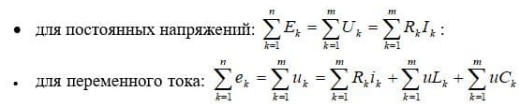
Обход контура совершается в произвольно выбранном направлении при соблюдении знаков для электродвижущей силы (ЭДС) и падений напряжения, входящих в уравнение.
Приведенное уравнение можно переписать
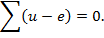
Следовательно, алгебраическая сумма напряжений на ветвях в любом замкнутом контуре равна нулю.
Для ЭЦ по законам Кирхгофа можно составить больше уравнений, чем это необходимо. Поэтому уравнения Кирхгофа составляются только для независимых узлов и независимых контуров ЭЦ.
Независимым узлом ЭЦ называется такой узел, который отличается от других хотя бы одной новой ветвью, подходящей к нему.
Независимым контуром ЭЦ называется такой контур, который отличается от других хотя бы одной новой ветвью, входящей в него.
2. Синусоидальные величины, их изображения, действующее, среднее и амплитудное значения. Связь вектора синусоидальной величины с ее мгновенными значениями.
Синусоидальная величина – это величина, изменяющаяся во времени по синусоидальному закону:
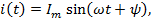
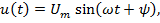
где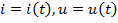 
– мгновенные величины;
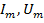– максимальное значение или амплитуда;
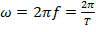– скорость изменения аргумента (угла) – угловая (круговая) частота, [рад/с или с-1];
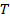– период – время, за которое совершается одно полное колебание, [с];
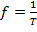– частота – число колебаний в 1 с, [Гц или с-1];
аргумент синуса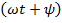 
называют фазовым углом или фазой – определяет стадию изменения функций;
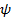– начальная фаза 
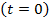, определяемая величиной смещения гармонической функции относительно начала координат.
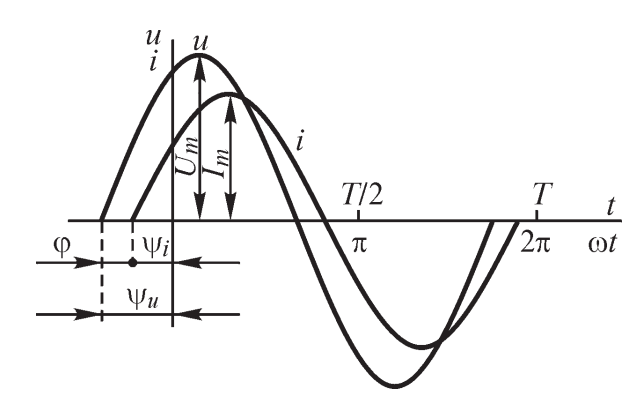
Действующее значение получается осреднением за период квадрата мгновенного тока (напряжения) и в математике называется среднеквадратическим значением.
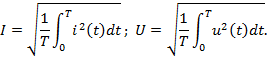
Действующее значение величины и его амплитуды связаны соотношением
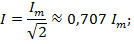
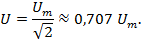
Под средним значением понимают среднее значение за полпериода.
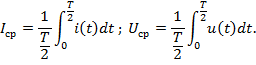
Среднее значение величины и его амплитуды связаны соотношением
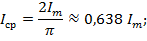
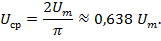
3. Комплексные величины. Векторные диаграммы.
Синусоидально изменяющуюся величину можно представить с помощью вектора на комплексной плоскости. Совокупность векторов, изображающих синусоидальные функции в заданный момент времени, называется векторной диаграммой.
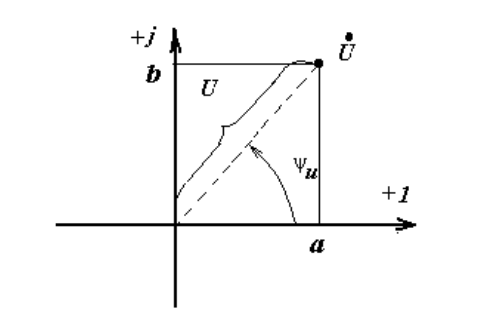
Комплексное число может быть представлено в алгебраической, тригонометрической и показательной форме:
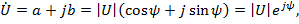
где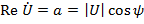 
– действительная часть,
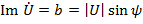– мнимая часть,
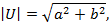
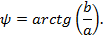
4. Основные законы линейных цепей переменного тока.
В цепях переменного тока закон Ома выполняется для всех значений, законы Кирхгофа – только для мгновенных и комплексных, которые учитывают фазные соотношения (сдвиг фаз).
5. Треугольник мощностей. Понятие активной, реактивной и полной мощностей.
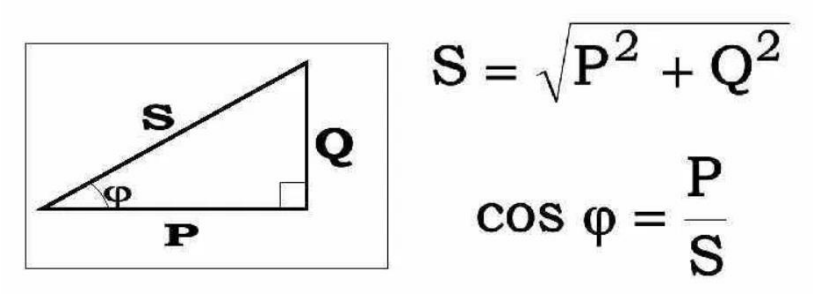
Среднее значение мгновенной мощности за период называется активной мощностью. Физический смысл средней мощности заключается в том, что она показывает мощность безвозвратно потребляемую цепью. Эта мощность выделяется в цепи либо в виде тепловой энергии в сопротивлении (нагревание резисторов), либо преобразуется в другие виды энергии. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную).
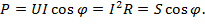
Реактивная мощность отражает процесс обмена энергией между источником энергии и совокупностью индуктивных и емкостных элементов.
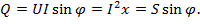
Полная мощность – это произведение действующих значений напряжения между выводами источника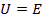 
и тока источника 
:
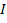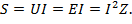
Отношение активной мощности к полной, равное косинусу угла сдвига фаз между напряжением и током, называется коэффициентом мощности:
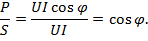
Активная, реактивная и полная мощность связаны соотношениями
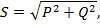
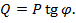
6. Законы Ома и Кирхгофа в комплексной форме.
7. Метод контурных токов.
Метод контурных токов предполагает в каждом независимом контуре схемы протекание контурного тока, знание которого позволяет найти все токи ветвей в схеме. В данном методе за неизвестные токи принимают контурные токи. Уравнения с контурными токами получают на основании второго закона Кирхгофа; их число равно числу независимых уравнений, составляемых для контуров, т.е.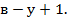 
Порядок расчёта:
* определяем независимые контуры и указываем направления отсчета контурных токов и действительных токов в ветвях;
* составляем систему уравнений для контурных токов;
* решаем полученную систему уравнений и определяем контурные токи;
* определяем действительные токи, как алгебраическую сумму контурных токов, протекающих в этой ветви с учетом собственного знака.
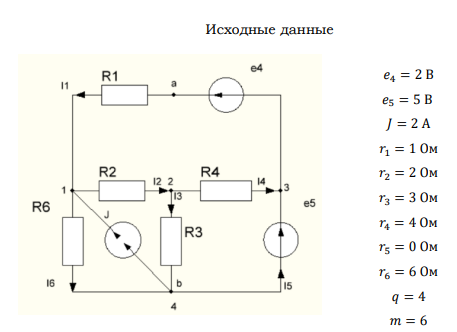
8. Метод узловых потенциалов.
Методом узловых потенциалов называют метод, в котором за неизвестные принимают потенциалы узлов схемы. Потенциал одного из узлов называемого базисным, принимается равным нулю, чтобы уменьшить количество неизвестных. В качестве базисного узла схем обычно выбирают узел, в котором соединяется наибольшее количество элементов или, (при наличии в схеме идеальных источников напряжения) узел, с которым соединяется один из зажимов идеального источника напряжения.
Данный метод основан на применении первого закона Кирхгофа и закона Ома. Число неизвестных равно числу уравнений, которые необходимо составить для схемы.
Для данного метода используется первый закон Кирхгофа, токи которого записываются с помощью закона Ома: потенциал*проводимость, где проводимость обратная величина сопротивлению.
Порядок расчета:
1. Определение количества независимых узлов и выбор направлений отсчета искомых токов в ветвях.
2. Выбор базисного узла.
3. Составление системы уравнений для узловых потенциалов.
4. Определение проводимостей узлов и узловых токов.
5. Решение системы линейных алгебраических уравнений и определение узловых потенциалов.
6. Расчет токов в ветвях цепи с использованием рассчитанных узловых потенциалов и законов Кирхгофа и Ома.
9. Индуктивно связанные элементы, их согласное и встречное включение
Если изменение тока в одном из элементов цепи приводит к появлению ЭДС в другом элементе цепи, говорят, что эти два элемента индуктивно связаны, а возникающую ЭДС называют ЭДС взаимной индукции.
Степень индуктивной связи двух элементов цепи характеризуют коэффициентом связи, под которым понимают отношение
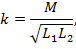
где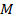 
– взаимная индуктивность элементов цепи;
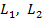– индуктивности элементов цепи.
Коэффициент связи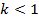 
всегда меньше единицы, т.к. витки двух катушек, так же как и различные витки одной катушки, пронизываются неодинаковыми магнитными потоками.
По определению индуктивность катушки
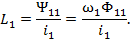
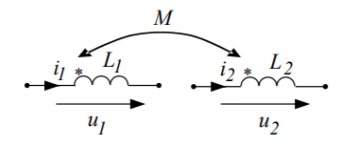
Согласным называют такое включение катушек, при котором их магнитные потоки, создающие ЭДС самоиндукции и взаимной индукции, имеют одинаковое направление, т.е. токи в обеих катушках направлены одинаково относительно одноименных зажимов: от начала к концу.
Встречным называют такое включение катушек, при котором их магнитные потоки, создающие ЭДС самоиндукции и взаимной индукции, имеют встречное направление, т.е. токи в обеих катушках направлены различно относительно одноименных зажимов: первая катушка - от конца к началу; вторая катушка – от начала к концу.
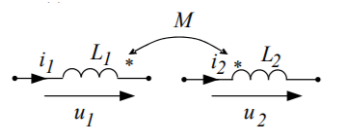
(Начало обмоток обычно обозначены звездочкой или точкой. То есть при согласном включении начало второй подключается к концу первой, а при встречном – конец второй присоединяется к концу первой.)
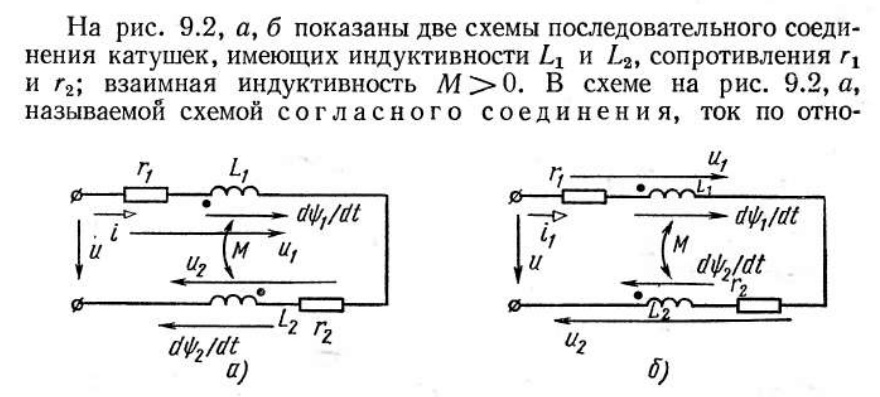
Напряжение на каждой из катушек содержит три составляющих: падение напряжения на активном сопротивлении, напряжение самоиндукции и напряжение взаимной индукции:
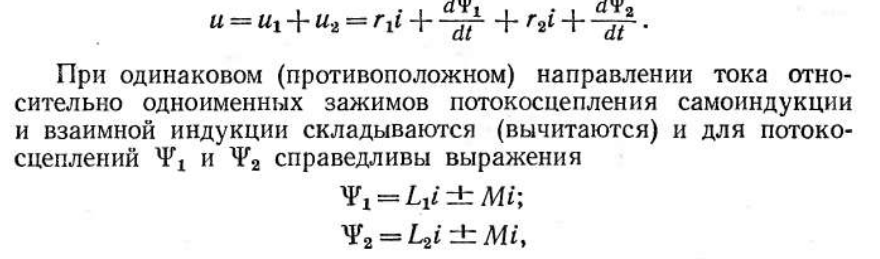
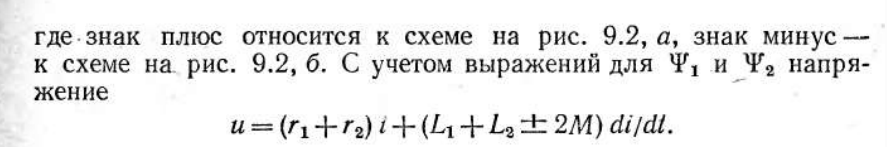
10. Закон Ома и векторная диаграмма для последовательной и параллельной R, L, C цепей.