Показникові та логарифмічні функції, рівняння, нерівності та їх системи.
1. Показникові та логарифмічна функції. Логарифм числа.
1.1 Знайдіть найменше ціле число, що входить в область визначення функції 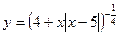 .
.
1.2.За яких значень 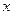 визначена функція
визначена функція 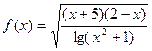 ?
?
1.3.Знайдіть найбільше ціле число, що входить в область визначення функції 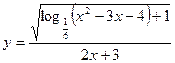 .
.
1.4. Знайдіть область визначення функції 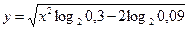 .
.
1.5. Знайдіть область визначення функції 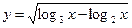 .
.
1.6. Обчисліть: 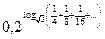
1.7. Дано 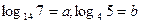 . Знайдіть
. Знайдіть 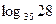
1.8. Обчисліть: 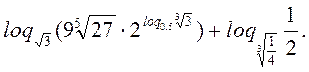
1.9. Обчисліть: 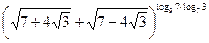 .
.
1.10. Обчисліть: 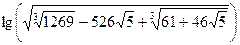 .
.
1.11. Обчисліть: 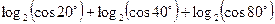 .
.
1.12. Обчисліть: 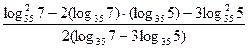
2. Розв’яжіть рівняння:
2.1. 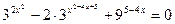
2.2. 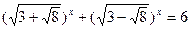
2.3. 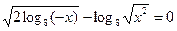
2.4. 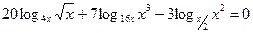
2.5. 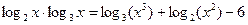
2.6. 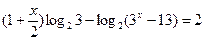
2.7. 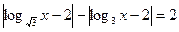
2.8. 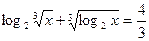
2.9. 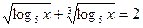
2.10. 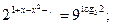
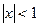
2.11. 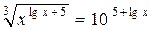 .
.
2.12. 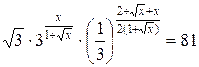
2.13. 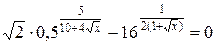 .
.
2.14. 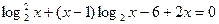 .
.
2.15. 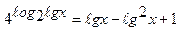 ;
;
2.16. 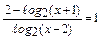 ;
;
2.17 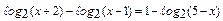
2.18. 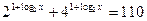
2.19. 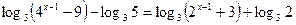
2.20. 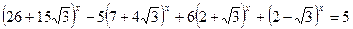
2.21. 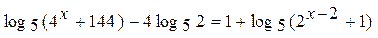
2.22. 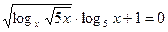
2.23. logx (2x2 - 4x + 3) = 2
2.24. lq x² = 0,25 lq (4x + 3x)4
2.25. 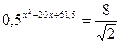
2.26. 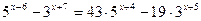
2.27. 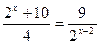
2.28. 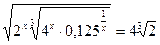
2.29. 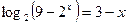
2.30 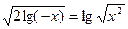
2.31. 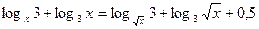
2.32. 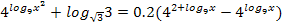
2.33. 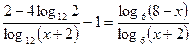
2.34. 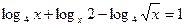
2.35 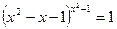
2.36. 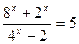
2.37. 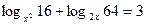
2.38. 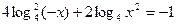
2.39. 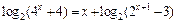
2.40. 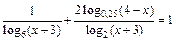 .
.
2.41. 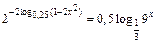 .
.
2.42. 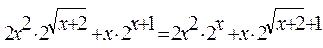
2.43. 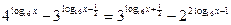 .
.
2.44. 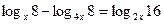 .
.
2.45. 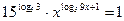
3. Розв’яжіть нерівності:
3.1. 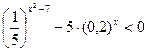
3.2. 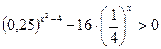
3.3. 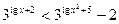
3.4. 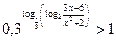
3.5. 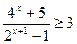
3.6. 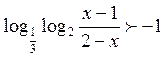
3.7. 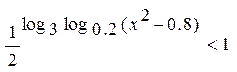
3.8. 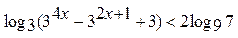
3.9. 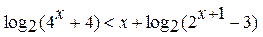
3.10. 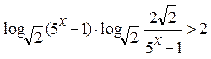
3.11. 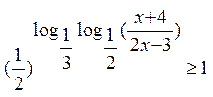
3.12. 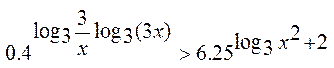
3.13. 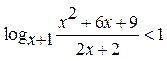
3.14. 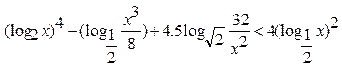
3.15. 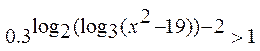
3.16. 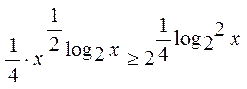
3.17. 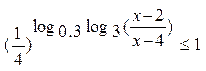
3.18. 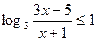
3.19. 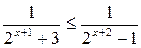
3.20. 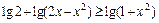
3.21. 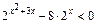
3.22. 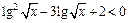
3.23. 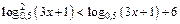 .
.
3.24. 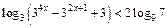 .
.
3.25. 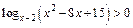 .
.
4. Розв’яжіть системи рівнянь:
4.1. 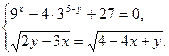
4.2. 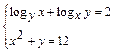
4.3. 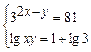
4.4. 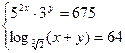
4.5. 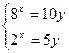
4.6. 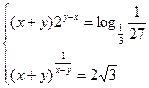
4.7. 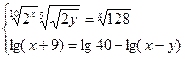
4.8. 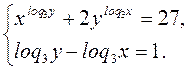
4.9. 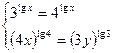
4.10. 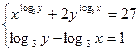
4.11. 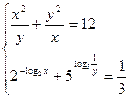
4.12. 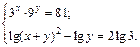
4.13. 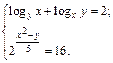
4.14. 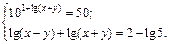
4.15. Знайти значення виразу 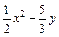 , де
, де 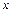 та
та 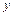 задовольняють систему рівнянь:
задовольняють систему рівнянь: 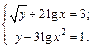
4.16. 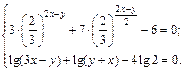
4.17. 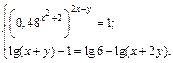
4.18. 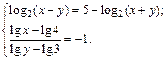
4.19. 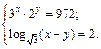
4.20. 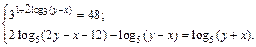
4.21. 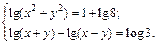
4.22. 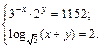
Розділ 4
Диференціальне та інтегральне числення функції однієї змінної
1. Знайдіть похідну функції:
1.1 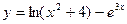
1.2. 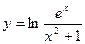
1.3. 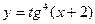
1.4. 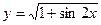
1.5. 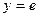
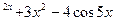
1.6. 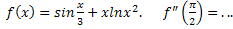
1.7. 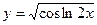
1.8. 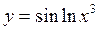
1.9. 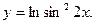
1.10. 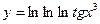
1.11. 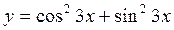
1.12. 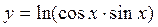
1.13. 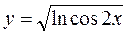
1.14. 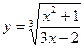
1.15. 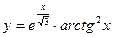
1.16. 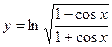
1.17. 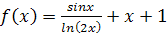
1.18. 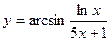
1.19. 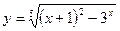
1.20. 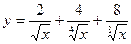
1.21. 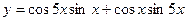
1.22. 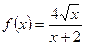
1.23 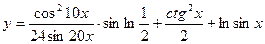
1.24. 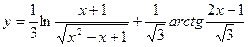
1.25. 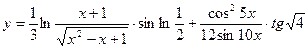
1.26. 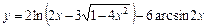
1.27. 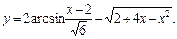
1.28. 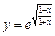
1.29. 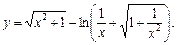
1.30. 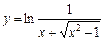
1.31. 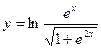
1.32. 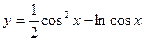
2. Застосування похідної.
2.1. Знайти проміжки зростання і спадання та точки екстремумів функції 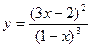 .
.
2.2. Знайти проміжки зростання і спадання та точки екстремумів функції 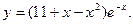
2.3. Знайти проміжки зростання і спадання та точки екстремумів функції 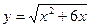
2.4. Знайти проміжки зростання і спадання та точки екстремумів функції 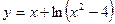
2.5. Знайти проміжки зростання і спадання та точки екстремумів функції 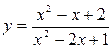 .
.
2.6. Знайти проміжки зростання і спадання та точки екстремумів функції 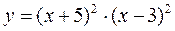
2.7. Знайти проміжки зростання і спадання та точки екстремумів функції 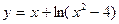
2.8. Дослідити на екстремум функцію 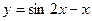 в інтервалі
в інтервалі 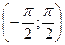 .
.
2.9. Знайти критичні точки функції 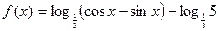
2.10. Знайти найменше та найбільше значення функції на заданому проміжку:
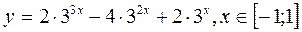 .
.
2.11. Знайти найменше та найбільше значення функції на заданому проміжку:
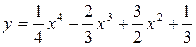 ;
; 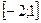
2.12. Знайти найменше та найбільше значення функції на заданому проміжку:
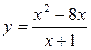 ,
, 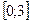 .
.
2.13. Знайдіть найменше значення функції 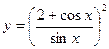 на проміжку
на проміжку 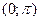 .
.
2.14. Знайти найменше та найбільше значення функції на заданому проміжку:
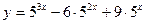 , якщо х є [–1;1];
, якщо х є [–1;1];
2.15. Знайти найменше та найбільше значення функції на заданому проміжку:
 , якщо х є [–1;3];
, якщо х є [–1;3];
2.16. Знайти найменше та найбільше значення функції на заданому проміжку:
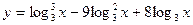 , якщо х є [9;243];
, якщо х є [9;243];
2.17. Знайти найменше та найбільше значення функції на заданому проміжку:
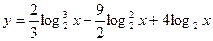 , якщо х є [
, якщо х є [ 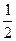 ;32].
;32].
2.18. Скласти рівняння дотичної до графіка функції 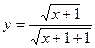 у точці з абсцисою
у точці з абсцисою 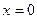 .
.
2.19. До кривої 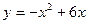 з точки М(3;10) проведені дві дотичні. Знайти кут між ними, та площу трикутника, утвореного цими дотичними та віссю Ох.
з точки М(3;10) проведені дві дотичні. Знайти кут між ними, та площу трикутника, утвореного цими дотичними та віссю Ох.
2.20. В точці 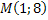 до кривої
до кривої 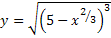 проведена дотична. Знайти довжину її відрізка, вміщеного між осями координат.
проведена дотична. Знайти довжину її відрізка, вміщеного між осями координат.
2.21. До графіка функції 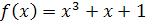 в точці з абсцисою
в точці з абсцисою 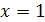 проведена дотична. Знайти абсцису точки графіка дотичної, ордината якої 31.
проведена дотична. Знайти абсцису точки графіка дотичної, ордината якої 31.
2.22. Залежність шляху від часу при прямолінійному русі точки задана рівнянням 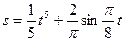 . Знайти швидкість точки через 2секунди після початку руху.
. Знайти швидкість точки через 2секунди після початку руху.
2.23. Дано функцію 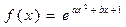 . Знайдіть значення сталих
. Знайдіть значення сталих 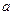 і
і 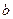 , якщо
, якщо 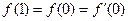 .
.
2.24. Дано функцію 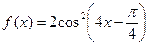 . Знайдіть область значень похідної
. Знайдіть область значень похідної 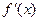 .
.
2.25.Знайдіть число розв’язків рівняння 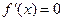 на відрізку
на відрізку 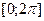 , де
, де 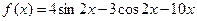 .
.
2.26. Знайдіть корені рівняння 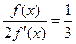 , якщо
, якщо 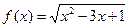 .
.
2.27. Знайти найменшу довжину (l) огорожі, за допомогою якої можна обгородити ділянку в формі прямокутника з даною площею (S), який прилеглий до стіни.
2.28. В прямокутний трикутник з гіпотенузою 8см і кутом 60° вписаний прямокутник, основа якого лежить на гіпотенузі. Якими повинні бути розміри прямокутника, щоб його площа була найбільшою?
2.29. Серед всіх рівнобічних трикутників з бічною стороною 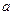 знайдіть трикутник найбільшої площі.
знайдіть трикутник найбільшої площі.
2.30. Знайти число, куб якого перевищує потрійний його квадрат на мінімальне значення.
2.31. Знайти додатне число, сума якого зі своєю оберненою величиною мала би найменше значення.
3. Інтегральне числення
3.1. Обчисліть інтеграл: 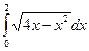 .
.
3.2. Обчисліть площу фігури, яка обмежена лініями 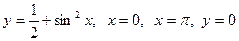 .
.
3.3. Обчисліть площу фігури, яка обмежена графіком функції 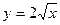 і дотичною, проведеною до графіка функції
і дотичною, проведеною до графіка функції 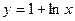 у точці з абсцисою
у точці з абсцисою 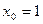 .
.
3.4. Обчисліть площу фігури, яка обмежена графіком функції 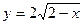 і дотичною, проведеною до графіка функції
і дотичною, проведеною до графіка функції 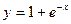 у точці з абсцисою
у точці з абсцисою 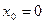 .
.
3.5. Обчисліть інтеграл: 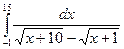 .
.
3.6. Обчисліть інтеграл: 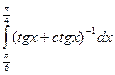 .
.
3.7. Обчисліть інтеграл: 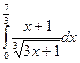 .
.
3.8. Обчисліть інтеграл: 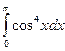 .
.
3.9. Знайти 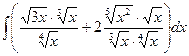
3.10. Обчисліть інтеграл: 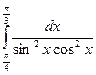 .
.
3.11. Обчисліть площу фігури, яка обмежена лініями 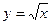 ,
, 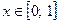 ,
, 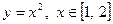 і
і 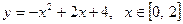 .
.
3.12. Обчисліть площу фігури, яка обмежена графіками функцій 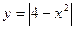 та
та 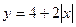 .
.
3.13. Обчисліть інтеграл: 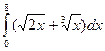 .
.
3.14. Знайти 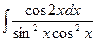
Розділ 5.
Геометричні задачі
Планіметрія
1. У коло радіуса R вписано трикутник з кутами 150 і 600. Знайдіть площу цього трикутника.
2. Коло, центр якого на гіпотенузі, торкається більшого катета трикутника і проходить через вершину протилежного гострого кута. Знайти його радіус, якщо катети 3 см і 4 см.
3. В прямокутний трикутник вписано півколо так, що діаметр кола лежить на гіпотенузі, а центр кола ділить гіпотенузу на відрізки 15 см і 20 см. Знайдіть площу трикутника.
4. Прямі, що містять бічні сторони рівнобічної трапеції перетинаються під прямим кутом. Знайти довжини сторін трапеції, якщо площа її 12 см 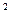 , а висота 2 см.
, а висота 2 см.
5. Знайти площу круга, вписаного в рівнобічну трапецію, якщо її більша основа дорівнює 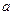 , а кут при меншій основі дорівнює 120
, а кут при меншій основі дорівнює 120 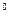 .
.
6. Площа рівнобічної трапеції, описаної навколо круга, дорівнює 8 см 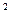 . Визначити сторони трапеції, якщо кут при основі дорівнює 30
. Визначити сторони трапеції, якщо кут при основі дорівнює 30 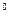 .
.
7. Площа рівнобічної трапеції, описаної навколо круга дорівнює S. Визначити бічну сторону, якщо гострий кут при основі дорівнює 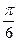 .
.
8. Довжини паралельних сторін трапеції 25 см та 4 см. А довжини непаралельних сторін 20см та 13см. Знайти висоту трапеції.
9. На гіпотенузі АВ прямокутного трикутника АВС вибрана точка К, для якої СК = ВС. Відрізок СК перетинає бісектрису АМ в її середині. Знайти кути трикутника АВС.
10. В рівнобедрений трикутник з основною 6 см і бічною стороною 5 см вписано коло. До кола проведено дотичну перпендикулярно основі. Знайти площу трикутника, який відсікає від даного трикутника ця дотична.
11. В трикутнику довжини двох сторін 6 і 3 см. Знайти довжину третьої сторони, якщо півсума висот, проведених до даної сторони дорівнює третій висоті.
12. Квадрат зі стороною a зрізаний по кутам так, що утворився правильний восьмикутник. Визначити площу цього восьмикутника.
13. Коло радіуса R вписане в рівнобічну трапецію. Верхня основа трапеції в два рази менша її висоти. Знайти площу трапеції.
14. Знайти висоту прямокутної трапеції, якщо її менша діагональ дорівнює більшій основі. Площа трапеції дорівнює S, гострий кут дорівнює α.
15. В квадрат ABCD вписаний інший квадрат KLMN, так що його вершини лежать на сторонах першого квадрата, а сторони складають зі сторонами першого квадрата кути по 30˚. Яку частину площі даного квадрата складає площа вписаного?
16. В прямокутнику ABCD сторона АВ в три рази більша сторони ВС. Всередині прямокутника лежить точка N, причому AN= 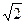 , BN=
, BN= 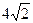 , DN=
, DN= 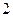 .Знайти косинус кута BAN і площу прямокутника ABCD.
.Знайти косинус кута BAN і площу прямокутника ABCD.
17. Визначити кут в ромбі, якщо його площа дорівнює Q, а площа вписаного круга дорівнює S.
18. Основи 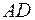 та
та 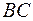 трапеції
трапеції 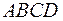 дорівнюють
дорівнюють 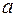 та
та 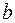
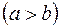 . Знайдіть довжину відрізка, який відрізається діагоналями трапеції на її середній лінії.
. Знайдіть довжину відрізка, який відрізається діагоналями трапеції на її середній лінії.
19. Довести, що в будь-якому трикутнику сума медіан 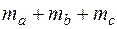 , більша
, більша 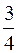 периметра, але менша периметра.
периметра, але менша периметра.
20. Прямокутний трикутник з катетами 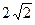 і
і 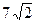 розділений прямою, перпендикулярною гіпотенузі на дві рівновеликі частини. Знайти довжину відрізка цієї прямої, що міститься в середині трикутника.
розділений прямою, перпендикулярною гіпотенузі на дві рівновеликі частини. Знайти довжину відрізка цієї прямої, що міститься в середині трикутника.
21. Медіани трикутника задовольняють умові 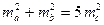 (
( 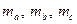 - медіани трикутника). Визначити тип трикутника.
- медіани трикутника). Визначити тип трикутника.
22. В трикутнику 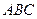 , такому, що
, такому, що 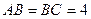 см і
см і 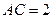 см, проведені бісектриса
см, проведені бісектриса 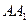 , медіана
, медіана 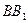 і висота
і висота 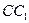 . Знайдіть площу трикутника, який утворено перетином прямих
. Знайдіть площу трикутника, який утворено перетином прямих 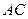 ,
, 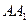 і
і 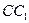 .
.
23. Площа трикутника АВС дорівнює 30 см2. На стороні АС взята точка Д так, що АД/ДС = 2/3. Довжина перпендикуляра ДЕ, опущеного на сторону ВС, дорівнює 9 см. Знайти ВС.
24. Знайти суму квадратів медіан трикутника, якщо відомі довжини його сторін а, в, с.
25. Обчислити координати ортоцентра трикутника, заданого вершинами А (1; 2); В (3; -1); С (-1; 0) користуючись тільки формулою відстані між двома точками.
26. Дано прямокутний трикутник з катетами 3 м і 4 м. Проведено круг так, що його діаметр збігається з більшим катетом. Обчислити площі частин круга, на які він розбивається гіпотенузою трикутника.
27. У правильний чотирикутник вписано круг, а в нього вписано правильний п’ятикутник. Знайти відношення площ цих багатокутників.
28. У прямокутній трапеції висота дорівнює 6 м, на бічній стороні (не перпендикулярній до основ), як на діаметрі, побудовано коло так, що воно дотикається до протилежної сторони трапеції. Обчислити площу прямокутного трикутника, у якого катети дорівнюють основам трапеції.
29. Діагональ BD чотирикутника ABCD є діаметром описаного навколо нього кола. Знайти довжину діагоналі АС, якщо BD=2 м, АВ=1 м, кут ABD відноситься до кута DBC як 4 до 3.
30. Дано трапецію з основами а і b . Знайти довжину відрізка MN, який з’єднує бічні сторони трапеції і паралельний до основ та ділить площу трапеції навпіл.
31. Коло, проведене на основі AD трапеції ABCD як на діаметрі, проходить через середини бічних сторін АВ і СD трапеції та дотикається до основи ВС. Знайдіть кути трапеції.
32. У паралелограмі зі сторонами а і b і гострим кутом α проведені бісектриси чотирьох кутів. Знайти площу чотирикутника, вершинами якого служать точки перетину бісектрис.
33. З кінців сторони трикутника 10 см проведено дві медіани довжиною 9 см і 12 см. Знайти дві інші сторони трикутника.
34. Дано дві сторони трикутника а, с. Знайти третю сторону цього трикутника, якщо його площа дорівнює 0,4ас.
35. У коло вписано чотирикутник MNPQ, діагоналі якого взаємно перпендикулярні і перетинаються в точці F. Пряма, що проходить через точку F і середину сторони NP, перетинає сторону MQ в точці Н. Знайдіть кут між прямими FH та MQ.
36. У коло радіуса R вписано трикутник з кутами 150 і 600. Знайти площу цього трикутника.
37. Сума кутів при більшій основі трапеції дорівнює 900. Основи трапеції рівні a та b. Знайти довжину відрізка, що сполучає середини основ трапеції.
38. Точка дотику кола вписаного в прямокутний трикутник ділить гіпотенузу на дві частини m і n. Знайти площу даного трикутника.
39. Діагоналі трапеції взаємно перпендикулярні, одна з них дорівнює 48см, а середня лінія трапеції – 25см. Знайдіть висоту трапеції.
40. Катети прямокутного трикутника дорівнюють 21см і 28см. Обчисліть площі частин трикутника, на які його ділить бісектриса прямого кута.
41. Бісектриса трикутника ділить сторону на відрізки 25см і 26см. Обчисліть відрізки, на які ділить цю сторону висота, довжина якої 72см.
42. Основа рівнобедреного трикутника дорівнює 36см, а бічна сторона – 54см. До бічних сторін трикутника проведено висоти. Обчисліть довжину відрізка, кінцями якого є основи висот.
43. Основа і бічна сторона рівнобедреного трикутника дорівнюють 20см і 30см відповідно. Знайдіть бісектрису кута при основі трикутника.
44. Діагональ рівнобічної трапеції ділить висоту, проведену з вершини тупого кута, на відрізки завдовжки 15см і 12см, а бічна сторона трапеції дорівнює її меншій основі. Знайдіть площу трапеції.
45. Катети прямокутного трикутника дорівнюють 6см і 8см. Знайдіть відстань від вершини меншого гострого кута трикутника до центра вписаного кола.
46. Основи рівнобічної трапеції дорівнюють 9см і 21см, а висота – 8см. Знайдіть радіус кола, описаного навколо даної трапеції.
47. Бісектриса кута А трикутника АВС (ÐС=90°) ділить катет ВС на відрізки завдовжки 6см і 10см. Знайдіть радіус кола, що проходить через точки А, С і точку перетину даної бісектриси з катетом ВС.
48. Центр кола, вписаного у прямокутну трапецію, віддалений від кінців її більшої бічної сторони на 15см і 20см. Обчисліть площу трапеції.
49. Катети прямокутного трикутника дорівнюють 18см і 24см. Знайдіть бісектрису трикутника, проведену з вершини меншого гострого кута.
50. Бічна сторона рівнобедреного трикутника дорівнює 4см, а медіана, проведена до цієї сторони, - 3см. Знайдіть периметр трикутника.
51. Діагональ рівнобічної трапеції перпендикулярна до бічної сторони і дорівнює 4см. Знайдіть площу трапеції, якщо радіус кола, описаного навколо неї, дорівнює 2,5см.
52. У рівнобедрений трикутник вписано коло, радіус якого дорівнює 10см, а точка дотику ділить бічну сторону на відрізки, довжини яких відносяться як 8:5, рахуючи від вершини рівнобедреного трикутника. Знайдіть площу цього трикутника.
53. Діагоналі рівнобічної трапеції є бісектрисами її гострих кутів і точкою перетину діляться у відношенні 5:13. знайдіть площу трапеції, якщо її висота дорівнює 9см.
54. Бісектриса кута А прямокутника АВСD ділить його сторону ВС на відрізки ВМ і МС завдовжки 10см і 14см відповідно. На відрізки якої довжини ця бісектриса ділить діагональ прямокутника?
55. Відрізок ВМ – медіана трикутника АВС, ВМ=m, ÐАВМ=a, ÐМВС=b. Знайдіть сторону АВ.
56. Центр кола, описаного навколо рівнобічної трапеції, лежить на її більшій основі. Знайдіть радіус цього кола, якщо діагональ трапеції дорівнює 20см, а її висота – 12см.
57. У трикутнику АВС АВ=ВС, ВD і АМ – висоти трикутника, ВD:АМ=3:1. знайдіть соsÐС.
58. Основи трапеції дорівнюють 2см і 6см, а бічні сторони – 13см і 15см. знайдіть площу трапеції.
59. У трикутнику АВС точка О – центр вписаного кола. Знайдіть радіус кола, описаного навколо цього трикутника, якщо АО=6см, ВО=10см, ÐС=60°.
60. Знайдіть радіус кола, описаного навколо рівнобічної трапеції, основи якої дорівнюють 11см і 21см, а бічна сторона – 13см.
Стереометрія
1. Бічна поверхня правильної трикутної піраміди в три рази більша площі основи. Площа круга, вписаного в основу, чисельно дорівнює радіусу цього круга. Знайти об’єм піраміди.
2. В правильній зрізаній трикутній піраміді сторона більшої основи 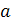 , а меншої –
, а меншої – 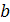 . Бічне ребро утворює з основою кут
. Бічне ребро утворює з основою кут 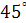 . Знайдіть площу перерізу, який проходить через бічне ребро і вісь піраміди.
. Знайдіть площу перерізу, який проходить через бічне ребро і вісь піраміди.
3. Основою піраміди SАВС є трикутник АВС, у якому АВ і АС утворюють між собою кут a і АВ = АС = а. Грань SВС перпендикулярна до площини основи, а грані SВА та SСА утворюють з площиною основи кути φ. Знайти бічну поверхню цієї піраміди.
4. В основі піраміди лежить прямокутний трикутник з периметром Р і гострим кутом 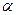 . Бічні ребра піраміди нахилені до площини основи під кутом
. Бічні ребра піраміди нахилені до площини основи під кутом 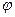 . Знайти об'єм піраміди.
. Знайти об'єм піраміди.
5. Обчислити об'єм правильної трикутної піраміди, якщо плоский кут при вершині дорівнює 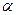 , а радіус кола, описаного навколо бічної грані дорівнює R.
, а радіус кола, описаного навколо бічної грані дорівнює R.
6. Дана піраміда, основою якої є прямокутний трикутник з гострим кутом 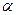 . Бічні ребра піраміди дорівнюють
. Бічні ребра піраміди дорівнюють 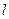 і нахилені до площини основи під кутом
і нахилені до площини основи під кутом 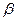 . Визначити об'єм піраміди.
. Визначити об'єм піраміди.
7. Дана піраміда, основою якої є прямокутний трикутник з гострим кутом 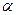 . Бічні ребра піраміди дорівнюють
. Бічні ребра піраміди дорівнюють 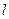 і нахилені до площини основи під кутом
і нахилені до площини основи під кутом 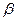 . Визначити об'єм піраміди.
. Визначити об'єм піраміди.
8. Основою чотирикутної піраміди є ромб, довжина меншої діагоналі якого рівна 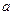 , а величина гострого кута рівна
, а величина гострого кута рівна 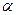 . Кожна бічна грань нахилена до площини основи під кутом
. Кожна бічна грань нахилена до площини основи під кутом 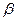 . Обчислити бічну поверхню піраміди.
. Обчислити бічну поверхню піраміди.
9. Діагональ бічної грані правильної трикутної призми рівна 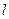 , і складає кут
, і складає кут 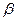 з площиною другої бічної грані. Знайти об'єм піраміди.
з площиною другої бічної грані. Знайти об'єм піраміди.
10. Визначити повну поверхню правильної трикутної піраміди, у якої плоский кут при основі бічної грані 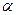 , а радіус круга, вписаного в основу, рівний
, а радіус круга, вписаного в основу, рівний 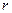 .
.
11. У зрізаному конусі діагоналі осьового перерізу взаємно перпендикулярні. Висота конуса дорівнює 6 см, а кут між твірною й площиною основи 60º. Знайдіть об'єм цього конуса.
12. Діагональ прямокутного паралелепіпеда дорівнює 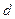 і утворює з площиною однієї бічної грані кут a, а іншої – кут b. Знайдіть площу бічної поверхні паралелепіпеда.
і утворює з площиною однієї бічної грані кут a, а іншої – кут b. Знайдіть площу бічної поверхні паралелепіпеда.
13. Апофема правильної чотирикутної піраміди дорівнює 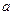 . Бічне ребро піраміди утворює з площиною основи кут a. Знайдіть об’єм піраміди.
. Бічне ребро піраміди утворює з площиною основи кут a. Знайдіть об’єм піраміди.
14. Через сторону правильного трикутника проведено площину. Яка утворює з площиною трикутника кут 30°. Знайдіть кути, які утворюють дві інші сторони трикутника з цією площиною.
15. Основа піраміди – рівнобедрений трикутник з бічною стороною 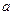 і кутом
і кутом 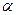 при основі. Бічна грань піраміди, що містить основу цього трикутника, перпендикулярна до площини основи, а дві інші нахилені до неї під кутом
при основі. Бічна грань піраміди, що містить основу цього трикутника, перпендикулярна до площини основи, а дві інші нахилені до неї під кутом 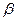 . Знайдіть об’єм піраміди.
. Знайдіть об’єм піраміди.
16. Через сторону нижньої основи і середину протилежного бічного ребра правильної трикутної призми проведено переріз під кутом 45° до площини основи. знайдіть об’єм призми. Якщо площа перерізу дорівнює 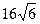 см
см 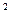 .
.
17. Через дві твірні конуса, кут між якими дорівнює 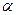 , проведено переріз, який утворює з площиною основи конуса кут
, проведено переріз, який утворює з площиною основи конуса кут 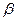 . Знайдіть площу бічної поверхні конуса.
. Знайдіть площу бічної поверхні конуса.
18. Основа прямої призми – ромб з гострим кутом 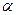 . Діагональний переріз призми, що проходить через більшу діагональ основи, має площу S. Знайдіть площу бічної поверхні призми.
. Діагональний переріз призми, що проходить через більшу діагональ основи, має площу S. Знайдіть площу бічної поверхні призми.
19. Через дві твірні конуса проведено площину, яка нахилена до площини його основи під кутом 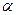 . Ця площина перетинає основу конуса по хорді, яку видно із центра його основи під кутом
. Ця площина перетинає основу конуса по хорді, яку видно із центра його основи під кутом 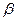 . Знайдіть площу бічної поверхні конуса, якщо його твірна дорівнює
. Знайдіть площу бічної поверхні конуса, якщо його твірна дорівнює 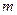 .
.
20. В правильній трикутній піраміді сума кутів, які утворені апофемою піраміди з площиною основи і бічним ребром з тією ж площиною, дорівнює 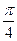 . Знайдіть ці кути.
. Знайдіть ці кути.
Завдання до поповнення архіву задач
Смілянський промислово-економічний коледж
1. Перетворенням лівої частини перевірити, що: 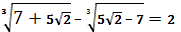
2. Довести тригонометричну тотожність: 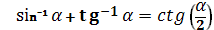
3. Довести, що 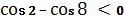
4. При якому значенні p(р 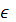 z) рівняння
z) рівняння
3 x 2 -4 x + p -2=0 і X 2 -2 px +5=0
мають спільний корінь? Знайти цей корінь.
5.Спростити:
5.1 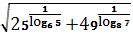
5.2 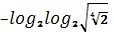
5.3 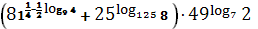
5.4 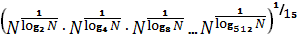
5.5 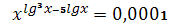
5.6 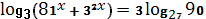
5.7 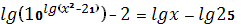
6.Знайти область визначення функції:
6.1 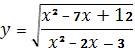
6.2 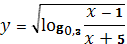
7. В яких точках дотичні до кривої 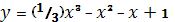 паралельні прямій y?
паралельні прямій y?
8. Прямолінійні рухи двох матеріальних точок задано рівняннями 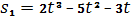 ,
, 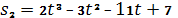 (). Знайти прискорення точок у той момент, коли їхні швидкості рівні між собою.
(). Знайти прискорення точок у той момент, коли їхні швидкості рівні між собою.
9. Знайти точки екстремуму функції 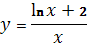
Викладач математики:
Півненко Світлана Володимирівна








