Контрольные вопросы
1. Чему равен угол фазового сдвига между напряжением и током:
а) для резистора;
б) для конденсатора;
в) для индуктивной катушки, у которой rk << w Lk?
2. Как опытным путем определить параметры пассивного двухполюсника?
3. Запишите все выражения, по которым можно рассчитать активную мощность в цепи синусоидального тока.
4. Изменением каких параметров можно настроить цепь в резонанс напряжений?
5. Какие опасные явления и при каких условиях могут сопровождать резонанс?
6. Чему равно полное сопротивление цепи (рис. 2.2) при резонансе?
7. Запишите формулы для вычисления добротности, коэффициента затухания и волнового сопротивления для цепи (рис. 2.2) при XL = XC ,
Литература: [3, с. 21, 45. 46; 4, с. 560: 1, с. 11, 20, 38; 5, с. 49-54, 59-64, 69-73, 316].
Лабораторная работа № 3
ПОВЫШЕНИЕ КОЭФФИЦИЕНТА МОЩНОСТИ В
ОДНОФАЗНОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА
Цель работы: ознакомиться с применением конденсаторов для компенсации реактивной составляющей тока активно-индуктивной нагрузки и с явлением резонанса токов.
Программа работы
1. Собрать электрическую цепь по схеме (рис.3.1) при отключенных конденсаторах (параметры приемника r и L устанавливаются преподавателем и при проведении всей работы остаются неизменными).
|
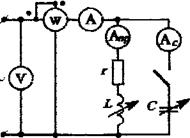
| Рис. 3.1. Повышение коэффициента мощности при помощи конденсаторов |
Измерить ток, напряжение, активную мощность и определить коэффициент мощности cos j и реактивную мощность Q . Данные измерений и вычислений занести в табл. 3.1.
Таблица 3.1
Измерение коэффициента мощности
| Пункт программы | С, мкФ | Измерено | Вычислено | |||||
| U, В | Р, Вт | I, А | Iпр, A | Ic, A | cos j | Q, вар | ||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 4 | ||||||||
По результатам измерений построить в масштабе векторную диаграмму токов и напряжения, указав на ней активную и реактивную составляющие тока и угол j.
2. Подключить конденсатор в цепи (рис. 3.1) (величина емкости С устанавливается преподавателем). Измерить токи, напряжение, активную мощность и вычислить коэффициент мощности цепи с конденсатором и реактивную мощность Q . Результаты измерений и вычислений занести в табл. 3.1.
3. Осуществить в цепи (см. рис. 3.1) режим резонанса токов. Для этого подобрать такое значение емкости конденсаторов, при котором выполняется условие Р » U × I , что соответствует cos j = 1.
В этом режиме измерить напряжение, токи, активную мощность, вычислить сшф и реактивную мощность, занести все эти данные в табл. 3.1.
4, Установить емкость больше, чем при резонансе, подключив параллельно еще один конденсатор. Убедиться, что cos j стал меньше, т.е. имеет место « перекомпенсация».
Измерить напряжение, активную мощность, токи. Вычислить коэффициент мощности, реактивную мощность. Занести эти данные в табл.3.1.
5, С помощью ЭВМ построить векторные и временные диаграммы тока и напряжения на входе цепи (рис. 3.1). Для режима п.4 определить с помощью векторной диаграммы знак угла j и знак реактивной мощности.
6, Для режима резонанса токов (п. 3) рассчитать необходимое значение емкости Срез,
Пояснения к работе
Энергетические процессы в электрической цепи синусоидального тока характеризуются понятиями:
- активная мощность ;
- реактивная мощность ;
- полная мощность ;
- коэффициент мощности ,
Все эти величины могут быть определены по измеренным току I, напряжению U и активной мощности Р на входе цепи. Для определения знака угла j необходимы дополнительные опыты.
В лабораторной работе исследуется параллельное соединение приемника и конденсаторов. Все опыты рекомендуется выполнять при неизменном напряжении сети, а при построении векторных диаграмм нужно это напряжение брать за основу, принимая его начальную фазу равной нулю (yи =0).
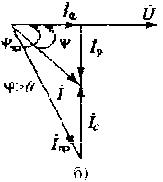
К пункту 1. Для нахождения активной и реактивной составляющих тока приемника на векторной диаграмме следует разложить вектор 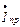 на две составляющие: параллельную и перпендикулярную вектору
на две составляющие: параллельную и перпендикулярную вектору 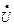 (рис. 3.2,а).
(рис. 3.2,а).
| 
|
| 
|
| в) | г) |
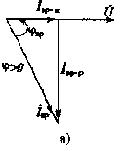
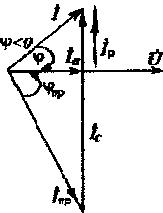
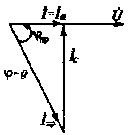
| Рис. 3.2. Векторные диаграммы при различных значениях емкости конденсаторов | |
К пункту 2. При подключении конденсатора в нем будет проходить ток емкостного характера, который находится в противофазе с реактивной составляющей тока приемника 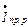 Поэтому реактивная составляющая тока на входе цепи
Поэтому реактивная составляющая тока на входе цепи 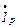 уменьшается. Это вызывает уменьшение утла j и увеличение cos j (рис. 3.2,6).
уменьшается. Это вызывает уменьшение утла j и увеличение cos j (рис. 3.2,6).
Уменьшается и ток 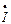 , что вызывает уменьшение потерь в линии электропередачи.
, что вызывает уменьшение потерь в линии электропередачи.
К пункту 3. При резонансе 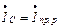 и реактивная составляющая тока на входе цепи
и реактивная составляющая тока на входе цепи 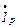 равна нулю, что соответствует j = 0 и cos j = 1 (рис. 3.2,в). Потребляемый ток минимален и равен активной составляющей тока приемника
равна нулю, что соответствует j = 0 и cos j = 1 (рис. 3.2,в). Потребляемый ток минимален и равен активной составляющей тока приемника 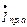 .
.
К пункту 4. При подключении большой емкости 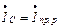 угол j меняет знак (j < 0). Ток в этом случае опережает напряжение, а коэффициент мощности уменьшается по сравнению с режимом резонанса (рис. 3.2,г).
угол j меняет знак (j < 0). Ток в этом случае опережает напряжение, а коэффициент мощности уменьшается по сравнению с режимом резонанса (рис. 3.2,г).
К пункту 5. Построение векторных и временных диаграмм осуществляется с помощью программы ЭВМ LAB3.mcd в системе MathCad после ввода результатов измерений и вычислений из табл. 3.1. Векторные диаграммы получаются при работе программы в виде векторов для каждого из режимов (пп. 1-4).
В отчете диаграммы должны быть представлены для всех режимов в виде (рис. 3.2) с указанием масштаба векторов и их обозначениями.
К пункту б. При резонансе 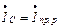 , и реактивная составляющая тока на входе цепи Ip = 0, что соответствует j = 0 и cos j = 1.
, и реактивная составляющая тока на входе цепи Ip = 0, что соответствует j = 0 и cos j = 1.
В программе LAB3.mcd по условию резонанса токов вычисляется точное значение емкости конденсатора Срез, которое необходимо сравнить с емкостью набранной на лабораторном стенде в режиме, принятом за резонанс токов при проведении эксперимента (п. 3).
Контрольные вопросы и задачи
1. Как изменится угол j и коэффициент мощности приемника, если:
а) увеличится активное сопротивление r;
б) увеличится индуктивность L?
2. Как изменятся потери в линии электропередачи после компенсации реактивной составляющей тока приемника, если напряжение U и активная мощность Р приемника остаются неизменны?
3. Поясните при помощи векторной диаграммы, почему изменяется cos j цепи при подключении конденсаторов.
4. Запишите соотношение между параметрами r, L , C цепи (см. рис. 3.1) на известной частоте f в режиме резонанса токов (реактивная проводимость b = 0).
5. С помощью векторной диаграммы найдите, каким будет ток в неразветвленной части цепи (рис. 3.1) в режиме резонанса токов, если активное сопротивление приемника r станет равным нулю?
6. Цепь находится в режиме резонанса токов (рис. 3.1). Определить знак реактивной мощности, если:
а) увеличить емкость С конденсаторов:
б) уменьшить емкость С конденсаторов.
Литература: [3, с. 114-122; 5, с. 73-77, 316, 86-89].
Лабораторная работа № 4








