Задание: выполнить задание математической разминки, изучить материал урока, выполнить самостоятельную работу, ответить на контрольные вопросы и выполнить домашнюю работу.
Информационная карта к уроку
Тема: Применение производной в исследовании функции для построения графика.
Цель: научиться исследовать функции с помощью производной и строить графики.
Задание: выполнить задание математической разминки, изучить материал урока, выполнить самостоятельную работу, ответить на контрольные вопросы и выполнить домашнюю работу.
1. Математическая разминка
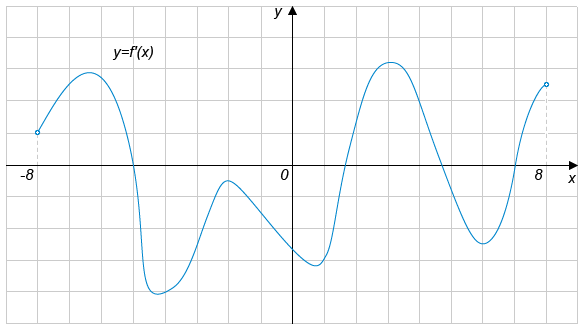
На рисунке изображён график производной функции y= f '(x), определенной на интервале (−8;8).
Найдите промежутки возрастания и убывания функции и количество точек экстремума функции f(x), принадлежащих отрезку [−4;6].
2. Теоретический минимум
1. Алгоритм нахождения промежутков монотонности
1) Найти производную функции f '(x) и найти точки, в которых производная не существует.
2) Решить уравнение f '(x) =0 и найти критические точки.
3) Нанести на числовую ось критические точки и найти знаки производной на полученных интервалах.
4) Выписать в ответ интервал возрастания (со знаком +) и интервал убывания (со знаком -).
2. Алгоритм нахождения экстремумов
1) Найти производную функции f '(x) и найти точки, в которых производная не существует.
2) Решить уравнение f '(x) =0 и найти критические точки.
3) Нанести на числовую ось критические точки и найти знаки производной на полученных интервалах.
4) Найти значения максимума (для точек, в окрестности которых меняется знак производной с + на - ) и значения минимума (для точек, в окрестности которых меняется знак производной с - на + ).
3. Алгоритм полного исследования функции
1) Найти область определения функции.
2) Найти область значений функции. Обычно этот пункт пропускают или заполняют после исследования на экстремумы.
3) Исследовать непрерывность функции, выделить особые точки (точки разрыва).
4) Найти точки пересечения с осями координат.
5) Найти нули функции.
6) Установить, является ли функция чётной или нечётной. Сделать выводы о симметричности графика функции.
7) Установить, является ли функция периодической или нет. Обычно проверяют для тригонометрических функций, для других данный пункт пропускается.
8) Найти первую производную. Найти точки экстремума и интервалы монотонности (возрастания и убывания) функции.
9) Найти дополнительные точки.
10) Построить график функции.
3. Выполнение упражнений
a) Исследуйте функцию и постройте ее график: f (x)= x4-2х2-3.
1) D (f) =R.
2) f(-x)= (-x)4-2(-x)2-3 = x 4-2х2-3; f(-x)= f(x),
значит, функция f является четной. Исследование ее можно проводить на промежутке [0;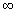 
).
3) Найдем точки пересечения графика функции с осями координат, то есть решим уравнение x 4-2х2-3 = 0. Пусть х2 =у, у2-2у-3= 0, у=3 или у=-1, то есть х2=3, х=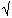 
3 или х=- 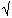3; х2=-1 не имеет решений. Получили две точки пересечения с осью абсцисс М( 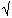3; 0), К(- 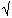3; 0). График пересекает ось ординат в точке В (0; -3).
4) Найдем производную f '(x) = 4x 3-4х = 4х(х-1)(х+1).
5) Найдем критические точки функции:
а) f ' (x) =0, если 4х (х-1) (х+1)=0, <=> x = 0; x = -1; x = 1.
б) f ' определена на всей D(f). - + - +
6) Определим знак производной на промежутках -1 0 1 (- 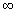; -1), (-1; 0), (0; 1), (1; ):
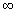а) f '(-2) = -32+8 < 0;
б) f '(-1/2) = 4 * (-1/2)3 -4 * (-1/2)= -1/2 + 2 > 0;
в) f '(1/2) = 4 * (1/2)3 -4 * (1/2)= 1/2 - 2 < 0;
г) f '(2) = 4 * 8 - 4 * 2 > 0.
Найдем значения функции в точках -1; 0; 1:
f (-1)=-4- min, f(0)=-3- max, f(1)=-4 -min.
Построим график (самостоятельно)
b) Найти число корней уравнения: 2x 3-3x 2-12х-11=0
Решение: Рассмотрим функцию f(x)= 2x 3-3x 2-12х-11=0.
1) Найдем область определения функции: D (f) = (- ; )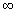
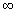2) Найдем ее производную: f '(x) = 6x 2-6х-12
3) Найдем критические точки функции:
f '(x) =0, если 6x 2-6х-12=0, <=> x = -1; x = 2.
4) На промежутке (- 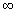; -1] функция возрастает от - 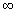до -4, поэтому на этом промежутке уравнение f (x)=0 корней не имеет.
На промежутке [-1; 2] уравнение так же не имеет корней, так как на этом промежутке функция убывает от -4 до -31.
На промежутке [2; 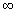) функция возрастает от -31 до бесконечности, на этом промежутке уравнение f (x)=0 имеет один корень (по теореме о корне, то есть если функция возрастает (убывает) на промежутке I, число а - любое из значений, принимаемых f на этом промежутке, то уравнение f (x) = а имеет единственный корень в промежутке I). Итак, уравнение 2x 3-3x 2-12х-11=0 имеет один корень и этот корень принадлежит интервалу (2; ).
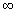c) Сколько корней имеет уравнение: x 4/4 -x 3- x 2/2 +3х = 0
Решение: Рассмотрим функцию f(x) = x 4/4 -x 3- x 2/2 +3х:
1) Найдем область определения функции D(f) = (- ; ).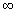
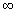2) Найдем производную f ' (x) = x 3- 3x 2 -x+3
3) Найдем критические точки и промежутки возрастания и убывания функции:
f ' (x) = 0 <=> x 3- 3x 2 -х+3=0 <=> x 2(х-3) -(х-3)=0 <=> (х-3)( x 2-1) = 0 <=> х=3, х1=1, х2=-1.
Рис. (знаки f ')
Из рисунка видно, что: f(x) возрастает на интервалах [-1; 1] и [3; + );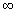
| y |
| x |
f(x) убывает на (- 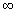; -1] и [1; 3].
4) Найдем точки экстремума и экстремумы функции:
х=-1 min f min= 1/4+1-1/2 -3=-9/4 < 0,
x= 1 max f max= 1/4 -1-1/2+3 =1 3/4 > 0,
х=3 min f min= 81/4-27-9/2+9= -27/2 < 0.
Строим эскиз графика
Из рисунка видно, что многочлен имеет 4 корня, следовательно, уравнение имеет 4 решения.
4. Самостоятельная работа.
Вариант I.
Пример 1. Исследуйте функцию f(x)= x3-3х2 и постройте ее график
Пример 2. Сколько корней имеет уравнение: x4 - 4x3 - 9 = 0.
Вариант II.
Пример 1. Исследуйте функцию y = 1/3x3- 3x2 + 8x и постройте ее график.
Пример 2. Сколько корней имеет уравнение: x2- x3/3- 1= 0
5. Контрольные вопросы:
1) Какие точки называются критическими?
2) Как связаны возрастание и убывание функции со знаком производной?
3) Как связаны знаки производной с экстремумами функции?
6. Д.З.: §51 № 926 – 927 (3-4)