Если множество принадлежит или евклидовой прямой, или евклидовой плоскости, говорят о функциях одной, двух, трех, …, n переменных.
1. Функции нескольких переменных, основные понятия
Если каждой точке М из некоторого множества 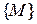 точек евклидова пространства ставится в соответствие по известному закону некоторое число
точек евклидова пространства ставится в соответствие по известному закону некоторое число 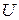 , то говорят, что на множестве
, то говорят, что на множестве 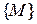 задана функция
задана функция 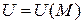 , или
, или 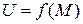 .
.
Если множество 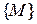 принадлежит или евклидовой прямой, или евклидовой плоскости, говорят о функциях одной, двух, трех, …, n переменных.
принадлежит или евклидовой прямой, или евклидовой плоскости, говорят о функциях одной, двух, трех, …, n переменных.
Пример 1.1 Площадь прямоугольника со сторонами, длины которых равны 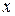 и
и 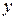 , выражается формулой
, выражается формулой 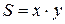 .
.
Пример 1.2. Объем 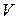 прямоугольного параллелепипеда с ребрами, длины которых равны
прямоугольного параллелепипеда с ребрами, длины которых равны 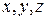 выражается формулой
выражается формулой 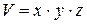 .
.
Пример 1.3. Величина силы притяжения 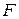 двух материальных точек, имеющих массы
двух материальных точек, имеющих массы 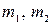 и занимающих соответственно положение
и занимающих соответственно положение 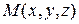 и
и 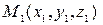 , согласно закону Ньютона равна
, согласно закону Ньютона равна
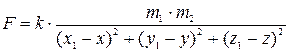 , где
, где 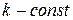 .
.
Следовательно, 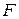 есть функция от шести переменных
есть функция от шести переменных 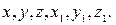
Всякая функция от нескольких переменных становится функцией от меньшего числа переменных, если часть переменных зафиксировать, то есть придать постоянные значения.
Например, пусть мы имеем функцию трех переменных 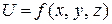 .
.
Если положить 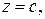 то мы получим функцию от двух переменных
то мы получим функцию от двух переменных 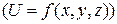 , если зафиксировать переменную
, если зафиксировать переменную 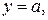 то получим функцию одной переменной
то получим функцию одной переменной 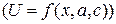 . Таким образом, в разных вопросах по желанию, функцию
. Таким образом, в разных вопросах по желанию, функцию 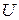 можно рассматривать как функцию одной, двух или трех переменных.
можно рассматривать как функцию одной, двух или трех переменных.
Геометрическим изображением (графиком) функции двух переменных 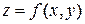 является, вообще говоря, поверхность в пространстве
является, вообще говоря, поверхность в пространстве 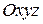 .
.
Линией уровня функции 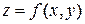 называется множество всех точек плоскости
называется множество всех точек плоскости 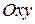 , для которых данная функция имеет одно и то же значение (изокривая). Ее уравнение
, для которых данная функция имеет одно и то же значение (изокривая). Ее уравнение 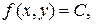 где
где 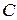 – некоторая постоянная. Поверхностью уровня функции
– некоторая постоянная. Поверхностью уровня функции 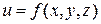 определяется уравнением
определяется уравнением 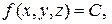 где
где 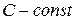 .
.
Пример 1.4. Соединив на карте поверхности Земли точки с одинаковой средней суточной температурой или давлением, получим соответственно изотермы и изобары, являющиеся важными исходными данными для прогноза погоды.
Пусть задана функция двух переменных 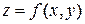
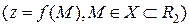 . Если зафиксировать переменную
. Если зафиксировать переменную 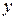 и дать переменной
и дать переменной 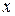 приращение
приращение 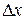 , то разность
, то разность 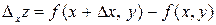 называется частным приращением функции
называется частным приращением функции 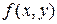 по переменной
по переменной 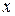 . Аналогично, зафиксировав переменную
. Аналогично, зафиксировав переменную 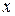 и дав приращение переменной
и дав приращение переменной 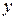 , получим частное приращение функции
, получим частное приращение функции 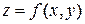 по
по 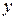 :
: 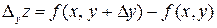 .
.
Придавая приращение сразу двум переменным 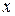 и
и 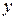 , можно получить полное приращение функции
, можно получить полное приращение функции 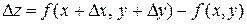 .
.
Пример 1.5. Найти полное приращение функции 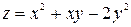 , где
, где 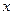 изменяется от 2 до 2,2 и
изменяется от 2 до 2,2 и 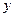 от 1 до 0,9.
от 1 до 0,9.
Решение. Приращения переменных: 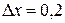 ,
, 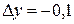 . Найдём значения функции в точках (2;1) и (2,2;0,9):
. Найдём значения функции в точках (2;1) и (2,2;0,9): 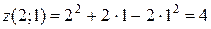 ,
, 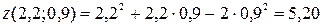 . Тогда полное приращение функции
. Тогда полное приращение функции 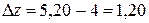 .
.
Частной производной функции от нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при условии, что последнее стремится к нулю.
Таким образом, по определению, для функций двух переменных
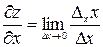 ;
; 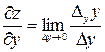 .
.
Пример 1.6. Пусть 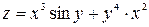 , тогда
, тогда 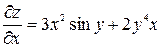 ;
; 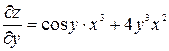 .
.
Функция 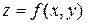 называется дифференцируемой в данной точке
называется дифференцируемой в данной точке 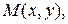 если ее полное приращение в этой точке может быть представлено в виде
если ее полное приращение в этой точке может быть представлено в виде 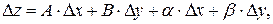 где А, В – некоторые не зависящие от
где А, В – некоторые не зависящие от 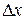 и
и 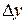 числа, а
числа, а 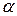 и
и 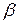 – бесконечно малые при
– бесконечно малые при 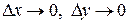 .
.
Полным дифференциалом функции 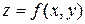 называется главная линейная часть полного приращения этой функции
называется главная линейная часть полного приращения этой функции 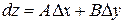 .
.
Если функция 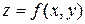 дифференцируема в точке
дифференцируема в точке 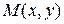 , то
, то 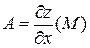 и
и 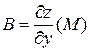 . Тогда
. Тогда 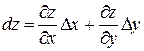 , или
, или 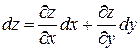 .
.
Пример 1.7. Найти дифференциал функции 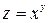 .
.
Решение. 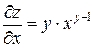 ,
, 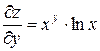 ,
,
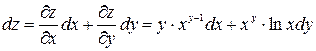 .
.
Частными производные второго порядка для функции 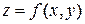 называются:
называются: 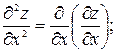
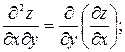
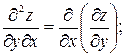
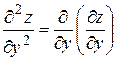 .
.
Продолжая таким путем дальше, можно определить частные производные третьего порядка, четвертого, …. Справедливо следующее утверждение: если все входящие в вычисления частные производные непрерывны, то смешанные частные производные не зависят от последовательности дифференцирования, т.е. в случае непрерывности, например 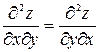 .
.
Пример 1.8. Пусть 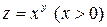 , тогда:
, тогда: 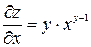 ;
; 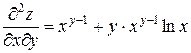 ;
; 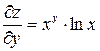 ;
; 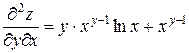 ;
; 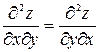 .
.
2. Экстремум функции нескольких переменных
Максимумом (минимумом) функции 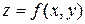 называется такое значение
называется такое значение 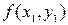 этой функции, которое больше (меньше) всех ее значений
этой функции, которое больше (меньше) всех ее значений 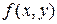 , принимаемой данной функцией в точках некоторой окрестности точки
, принимаемой данной функцией в точках некоторой окрестности точки 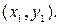 Максимум или минимум функции
Максимум или минимум функции 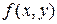 называется экстремумом этой функции, точка, в которой достигается экстремум, называется точкой экстремума:
называется экстремумом этой функции, точка, в которой достигается экстремум, называется точкой экстремума:
а) Необходимый признак экстремума: в точке экстремума функции нескольких переменных каждая ее частная производная первого порядка либо равна нулю, либо не существует 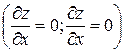 . Точки, в которых частные производные первого порядка равна нулю, либо не существуют, называются критическими;
. Точки, в которых частные производные первого порядка равна нулю, либо не существуют, называются критическими;
б) Достаточный признак экстремума: если точка 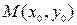 – критическая точка функции
– критическая точка функции 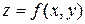 и
и 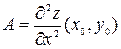 ,
, 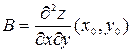 ,
, 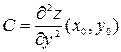 ,
, 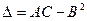 , тогда:
, тогда:
1) если 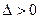 , то функция имеет экстремум в точке
, то функция имеет экстремум в точке 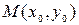 , а именно максимум, если
, а именно максимум, если 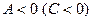 , и минимум, если
, и минимум, если 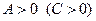 ;
;
2) если 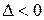 , то экстремума в точке
, то экстремума в точке 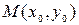 нет;
нет;
3) если 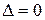 , то вопрос о наличии экстремума в точке
, то вопрос о наличии экстремума в точке 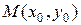 требует дополнительного исследования.
требует дополнительного исследования.
Пример 2.1. Исследовать на экстремум функцию 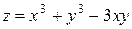 .
.
Решение. а) Найдем критические точки:
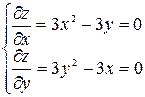
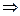
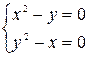
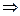
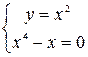
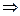
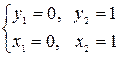
Таким образом, имеем две критические точки 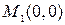 и
и 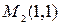 . Находим
. Находим 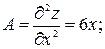
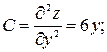
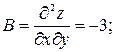
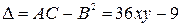 .
.
В точке 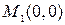
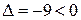 , т.е. в этой точке экстремума нет. В точке
, т.е. в этой точке экстремума нет. В точке 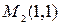
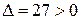 и
и 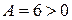 , следовательно, в этой точке функция имеет локальный минимум:
, следовательно, в этой точке функция имеет локальный минимум: 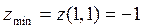 .
.
3. Градиент, производная по направлению
Если каждой точке М пространства или некоторой его области V поставлена в соответствие скалярная величина u(М), то говорят, что в этой области задано скалярное поле. В декартовой системе координат задание скалярного поля эквивалентно заданию функции трех переменных u(М) = u(x , y , z). Примерами скалярных полей могут служить поле температур данного тела, поле атмосферного давления и т.д. Пусть функция u(x , y , z) является непрерывно дифференцируемой в области V. В каждой точке этой области определен вектор, проекциями которого на оси координат являются значения частных производных функции u(x , y , z):
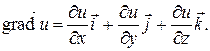
Вектор 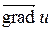 направлен в сторону наибыстрейшего возрастания скалярного поля u(М), а длина градиента равна наибольшей скорости изменения поля u в точке М.
направлен в сторону наибыстрейшего возрастания скалярного поля u(М), а длина градиента равна наибольшей скорости изменения поля u в точке М.
Рассмотрим в области V функцию u=u(x,y,z) и точку M(x,y,z). Проведем из точки M вектор 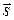 , направляющие косинусы которого cosa, cosb, cosg (косинусы углов, которые вектор образует с осями координат). Производной функции u=u(x,y,z) в точке M в направлении вектора
, направляющие косинусы которого cosa, cosb, cosg (косинусы углов, которые вектор образует с осями координат). Производной функции u=u(x,y,z) в точке M в направлении вектора 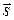 называется предел
называется предел
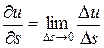 .
.
Если функция u=u(x,y,z) дифференцируема, то производная в данном направлении вычисляется по формуле:
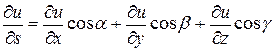 .
.
В случае функции двух переменных z=f(x,y) производная в данной точке M(x,y) направлении вектора 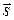 :
:
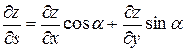 ,
,
где a – угол, образованный вектором с осью OX.
Производная по направлению 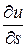 дает скорость изменения функции в данном направлении
дает скорость изменения функции в данном направлении 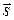 .
.
Градиентом функции z=f(x,y) в данной точке M(x,y) является вектор, координатами которого являются значения частных производных функции в заданной точке, то есть
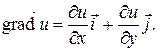
Пример 3.1. Дана функция 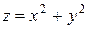 , точка
, точка 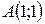 и вектор
и вектор 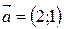 . Найти:
. Найти:
1) 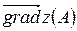 ;
;
2) Производную функции 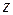 в точке
в точке 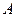 по направлению вектора
по направлению вектора 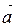 .
.
Решение. 1) Найдём частные производные функции 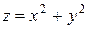 :
:
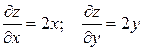 .
.
Значения частных производных в точке А: 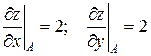 .
.
Следовательно, 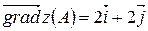 .
.
2) Найдём длину вектора 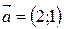 :
: 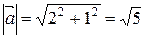 .
.
Направляющие косинусы вектора 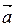 :
: 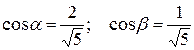 .
.
Производная по направлению:
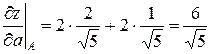 .
.
Пример 3.2. Найти градиент и производную функции 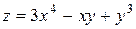 в точке А(1;2) по направлению вектора
в точке А(1;2) по направлению вектора 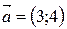 .
.
Решение. Найдём частные производные функции 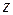 :
:
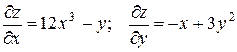 .
.
Значения частных производных в точке А:
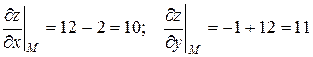 .
.
Тогда 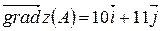 .
.








