Экстремум также может существовать в точках, в которых первые частные производные функции не существуют. Например, очевидно, что функция имеет минимум в точке .
Лекция 9.
2.14. Экстремумы функций нескольких переменных.
Точка 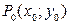 называется точкой экстремума (максимума или минимума) функции
называется точкой экстремума (максимума или минимума) функции 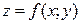 , если
, если 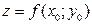 есть соответственно наибольшее или наименьшее значение функции
есть соответственно наибольшее или наименьшее значение функции 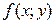 в некоторой окрестности точки
в некоторой окрестности точки 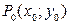 .
.
Значение функции в этой точке называется экстремальным.
Экстремальные точки всегда принадлежат области определения функции.
Теорема. (Необходимый признак существования экстремума в точке.) Если в точке 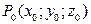 дифференцируемая функция
дифференцируемая функция 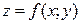 , имеет экстремум, то частные производные в этой точке равны нулю.
, имеет экстремум, то частные производные в этой точке равны нулю.
При этом обратное утверждение неверно, то есть, если частные производные в некоторой точке равны нулю, то экстремума у функции в этой точке может и не быть.
Экстремум также может существовать в точках, в которых первые частные производные функции не существуют. Например, очевидно, что функция 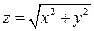 имеет минимум в точке
имеет минимум в точке 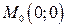 .
.
Однако, в этой точке ее производные 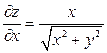 и
и 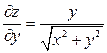 не существуют.
не существуют.
Точки функции, в которых ее первые частные производные обращаются в ноль или не существуют, называются критическими. Как следует из рассмотренной теоремы, экстремум существует не во всякой критической точке. Наиболее простым достаточным условием существования экстремума в критической точке 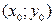 является следующий.
является следующий.
Назовем детерминантом 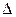 выражение вида:
выражение вида: 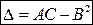 , где
, где
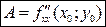 ;
; 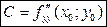 ;
; 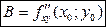 - значения частных производных второго порядка в исследуемой критической точке
- значения частных производных второго порядка в исследуемой критической точке 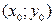 .
.
Замечание. Значения несмешанных частных производных в критических точках 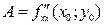 и
и 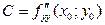 всегда имеют одинаковые знаки.
всегда имеют одинаковые знаки.
Тогда:
Если 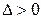 , то функция
, то функция 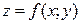 в этой критической точке имеет экстремум, при этом:
в этой критической точке имеет экстремум, при этом:
экстремум является максимумом, если 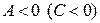 ,
,
экстремум является минимумом, если 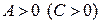 .
.
Если 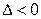 , то функция
, то функция 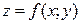 в этой критической точке не имеет экстремума.
в этой критической точке не имеет экстремума.
Если 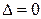 , то данный признак не дает ответа о наличии или отсутствии экстремума в точке.
, то данный признак не дает ответа о наличии или отсутствии экстремума в точке.
В последнем случае, а так же в случае, когда число переменных у функции более двух, вопрос о существовании экстремума решается на основе исследования знака дифференциала второго порядка.
Если в окрестности точки 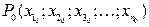
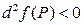 , то в точке максимум.
, то в точке максимум.
Если в окрестности точки 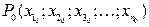
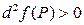 , то в точке минимум.
, то в точке минимум.
Если в окрестности точки 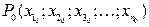
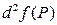 меняет знак, то в точке экстремума нет.
меняет знак, то в точке экстремума нет.
Пример 1. Найти экстремумы функции 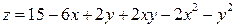 .
.
1. Найдем первые частные производные функции: 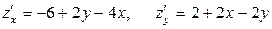 .
.
2. Найдем критические точки функции, для чего приравняем найденные производные к нулю и решим получившуюся систему уравнений:
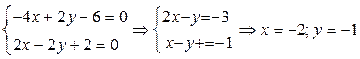 .
.
Таким образом, функция имеет одну критическую точку: 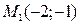 .
.
3. Найдем частные производные второго порядка и их значения в критической точке.
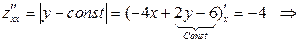
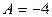 .
.
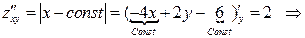
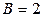 .
.
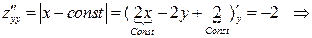
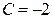 .
.
4. Найдем значения детерминанта в критической точке и определим наличие и характер экстремума.
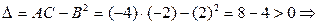 в точке
в точке 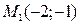 экстремум еcть. Так как
экстремум еcть. Так как 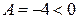 , то экстремум является максимумом.
, то экстремум является максимумом.
5. Найдем значения локальных экстремумов, подставив координаты экстремальных точек в заданную функцию: 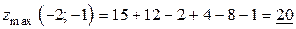 .
.
Пример 2.Найти экстремумы функции 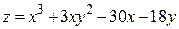 .
.
1. Найдем первые частные производные функции:
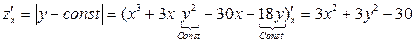 .
.
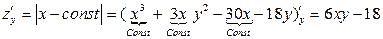 .
.
2. Найдем критические точки функции, для чего приравняем найденные производные к нулю и решим получившуюся систему уравнений:
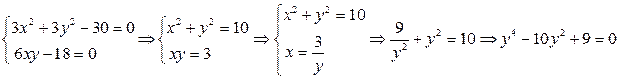 .
.
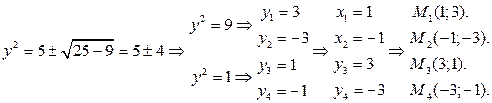
Значит, функция имеет четыре критические точки: 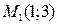 ;
; 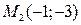 ;
; 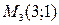 ;
; 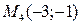 .
.
3. Найдем частные производные второго порядка и их значения в критических точках.
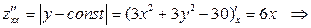
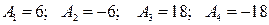 .
.
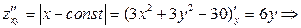
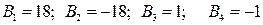 .
.
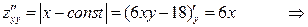
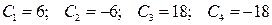 .
.
4. Найдем значения детерминантов в критических точках и определим наличие и характер экстремумов.
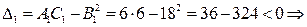 в точке
в точке 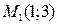 экстремума нет.
экстремума нет.
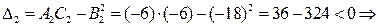 в точке
в точке 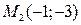 экстремума нет.
экстремума нет.
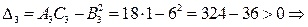 в точке
в точке 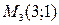 экстремум еcть. Так как
экстремум еcть. Так как 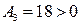 , то экстремум является локальным минимумом.
, то экстремум является локальным минимумом.
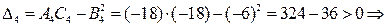 в точке
в точке 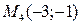 экстремум еcть. Так как
экстремум еcть. Так как 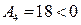 , то экстремум является локальным максимумом.
, то экстремум является локальным максимумом.
5. Найдем значения экстремумов, подставив координаты экстремальных точек в заданную функцию.
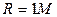
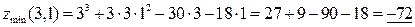 .
.
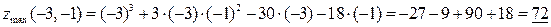 .
.
2.15. Условный экстремум.
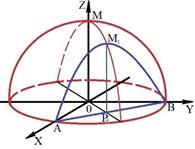 Понятие условного экстремума поясним на примере. Рассмотрим функцию
Понятие условного экстремума поясним на примере. Рассмотрим функцию 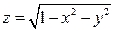 . Графиком этой функции является верхняя полусфера радиусом
. Графиком этой функции является верхняя полусфера радиусом 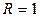 .
.
Очевидно, что эта функция имеет максимум равный единице в точке 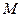 , которой в плоскости
, которой в плоскости 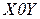 соответствует начало координат
соответствует начало координат 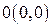 . Проведем прямую
. Проведем прямую 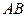 , уравнением которой будет
, уравнением которой будет 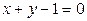 . Геометрически ясно, что для точек этой прямой наибольшее значение функции достигается в точке
. Геометрически ясно, что для точек этой прямой наибольшее значение функции достигается в точке 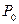 , лежащей посередине отрезка
, лежащей посередине отрезка 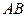 и имеющей координаты
и имеющей координаты 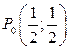 . Значение функции в этой точке и называется условным экстремум функции
. Значение функции в этой точке и называется условным экстремум функции 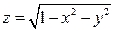 при условии, что
при условии, что 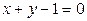 . Уравнение, выражающее условие, при котором ищется экстремум, называется уравнением связи.
. Уравнение, выражающее условие, при котором ищется экстремум, называется уравнением связи.
В общем случае задача выглядит так. Имеется некоторая функция 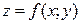 , описывающая некоторую поверхность, и плоская линия
, описывающая некоторую поверхность, и плоская линия 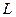 , расположенная в плоскости
, расположенная в плоскости 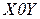 и описываемая уравнением связи
и описываемая уравнением связи 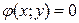 . Задача состоит в том, чтобы найти на линии
. Задача состоит в том, чтобы найти на линии 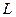 , точку
, точку 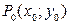 , в которой значение функции
, в которой значение функции 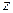 является наибольшим или наименьшим по сравнению со значениями этой функции в точках линии
является наибольшим или наименьшим по сравнению со значениями этой функции в точках линии 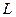 , лежащих вблизи точки
, лежащих вблизи точки 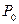 . Точка
. Точка 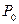 называется точкой условного экстремума, а значение функции
называется точкой условного экстремума, а значение функции 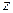 в этой точке условным экстремумом.
в этой точке условным экстремумом.
Существует три метода нахождения условного экстремума.
1. Если из уравнения связи 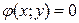 можно выразить одну переменную через другую, например,
можно выразить одну переменную через другую, например, 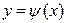 , то подставляя выражение
, то подставляя выражение 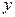 в функцию
в функцию 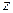 , получим функцию одной переменной
, получим функцию одной переменной 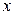 :
: 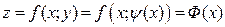 . Далее, исследуя эту функцию на экстремум, как функцию одной переменной, находим
. Далее, исследуя эту функцию на экстремум, как функцию одной переменной, находим 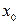 , а
, а 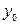 находим из уравнения связи
находим из уравнения связи 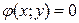 . Так для выше рассмотренного примера получим:
. Так для выше рассмотренного примера получим:
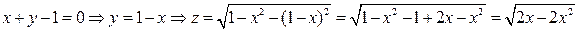 .
.
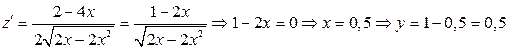 .
.
Таким образом, точка экстремума 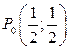 . Тогда значение экстремума равно:
. Тогда значение экстремума равно:
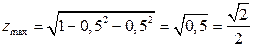 при условии
при условии 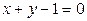 .
.
2. Если уравнение связи задано параметрическом виде: 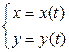 , то, подставив эти уравнения в уравнение функции, получим функцию одной переменной
, то, подставив эти уравнения в уравнение функции, получим функцию одной переменной 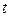 :
: 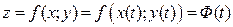 . Далее, исследуя эту функцию на экстремум, как функцию одной переменной
. Далее, исследуя эту функцию на экстремум, как функцию одной переменной 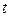 , находим значения параметра, при которых функция
, находим значения параметра, при которых функция 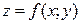 имеет условный экстремум. Значения
имеет условный экстремум. Значения 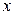 и
и 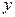 определяются из параметрических уравнений связи.
определяются из параметрических уравнений связи.
3. Если уравнение связи имеет более сложный вид, то для нахождения условного экстремума составляется функция Лагранжа, имеющая вид: 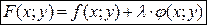 , где
, где 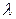 некоторый неопределенный коэффициент. Нахождение условного экстремума сводится в этом случае к решению системы из трех уравнений с тремя неизвестными
некоторый неопределенный коэффициент. Нахождение условного экстремума сводится в этом случае к решению системы из трех уравнений с тремя неизвестными 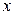 ,
, 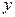 и
и 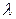 :
:
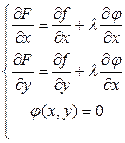 Вопрос о характере экстремума для полученных из решения системы значений
Вопрос о характере экстремума для полученных из решения системы значений 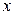 ,
, 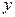 и
и 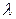 решается на основании изучения знака дифференциала второго порядка функции Лагранжа (см. раздел 1.11):
решается на основании изучения знака дифференциала второго порядка функции Лагранжа (см. раздел 1.11):
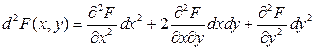 .
.
При этом 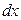 и
и 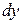 связаны уравнением:
связаны уравнением: 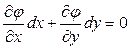 , при чем
, при чем 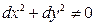 ;
; 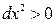 ;
; 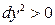 .
.
Пример. Найти экстремумы функции 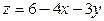 . При условии, что
. При условии, что 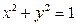 .
.
1. Составим функцию Лагранжа и найдем ее первые частные производные.
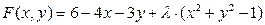 .
. 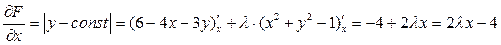 .
.
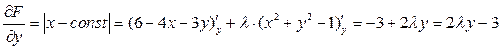 .
.
2. Составим систему из трех уравнений с тремя неизвестными и решим ее:
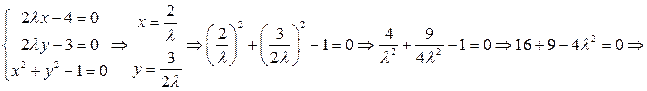
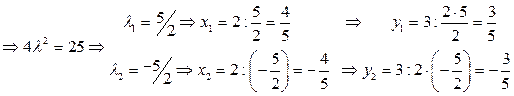
Тогда критические точки функции Лагранжа: 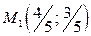 при
при 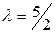 и
и 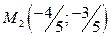 при
при 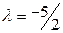 .
.
3. Найдем частные производные второго порядка функции Лагранжа и их значения в критических точках.
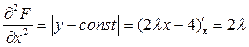 .
. 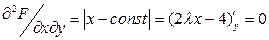 .
.
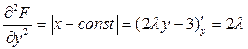 .
.
4. Определим знак дифференциала второго порядка функции Лагранжа в найденных точках.
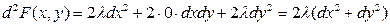 .
.
Тогда при 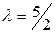 значение
значение 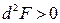 и в точке
и в точке 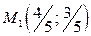 функция имеет условный минимум, а при
функция имеет условный минимум, а при 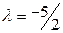 значение
значение 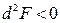 и в точке
и в точке 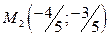 функция имеет условный максимум.
функция имеет условный максимум.
5. Найдем значения условных экстремумов:
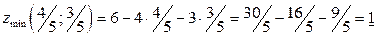 .
.
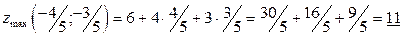 .
.
2.16. Наибольшее и наименьшее значения функции нескольких переменных.
Теорема. Если функция 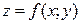 , непрерывна и дифференцируема в ограниченной замкнутой области, то она имеет в этой области наибольшее и наименьшее значения.
, непрерывна и дифференцируема в ограниченной замкнутой области, то она имеет в этой области наибольшее и наименьшее значения.
Для того, чтобы найти наибольшее  и наименьшее
и наименьшее 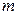 значения функции
значения функции 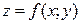 , в ограниченной и замкнутой области следует:
, в ограниченной и замкнутой области следует:
1. Найти критические точки функции и ее значения в этих точках.
2. Взяв в качестве уравнений связи, уравнения границ области найти условные экстремумы функции.
3. Найти значения функции в крайних точках границ.
4. Выбрать из всех найденных значений набольшее  и наименьшее
и наименьшее 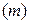 значения.
значения.
Пример. Найти наибольшее и наименьшее значения функции 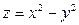 в круге
в круге 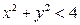 .
.
1. Найдем критические точки функции и ее значения в этих точках.
 у функции одна критическая точка:
у функции одна критическая точка: 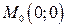 .
.
Значение функции в этой точке 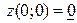 .
.
2. Найдем условные экстремумы, взяв в качестве уравнения связи уравнение 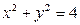 .
.
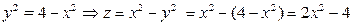 .
.
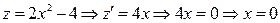 .
.
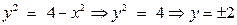 .
.
Имеем две критические точки 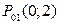 ,
, 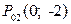 в которых значения функции равны:
в которых значения функции равны:
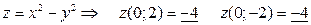 .
.
3. Так как область определения представляет собой круг радиуса 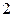 , то границы находятся в пределах:
, то границы находятся в пределах:
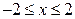 и
и 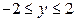 , и имеется четыре граничные точки:
, и имеется четыре граничные точки: 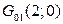 ,
, 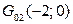 ,
, 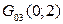 ,
, 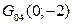 , из которых две последние совпадают с точками
, из которых две последние совпадают с точками 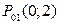 и
и 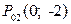 , рассмотренными в пункте 2.
, рассмотренными в пункте 2.
Найдем значения функции в точках 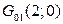 и
и 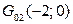 :
: 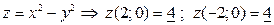 .
.
4. Таким образом, наибольшее и наименьшее значения должны выбираться из следующих значений функции: 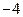 ;
; 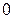 ;
; 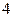 . Следовательно:
. Следовательно:
Наибольшее значение функции 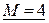 и достигается в точках
и достигается в точках 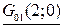 и
и 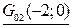 .
.
Наименьшее значение функции 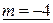 и достигается в точках
и достигается в точках 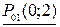 и
и 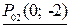 .
.
2.17. Задание №9 на практические занятия и самостоятельную работу.
Решить самостоятельно на занятии: Б.П.Демидович «Задачи и упражнения по математическому анализу» №2008, 2010, 2011, 2012; 2021, 2022; 2030; 2031. В задачнике Демидовича Б.П. есть краткая теория и разобранные примеры. Ответы в конце задачника.
Решить дома: Г.Н.Берман «Сборник задач по курсу математического анализа» №3271, 3272, 3273; 3292; 3280, 3281. Ответы в конце задачника. Подготовиться к контрольной работе.
2.18. Пробный вариант контрольной работы №4 «Функции нескольких переменных».
1. Найти область определения функции и изобразить ее на плоскости 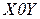 :
: 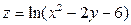 .
.
2. Найти полный дифференциал функции 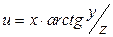 .
.
3. 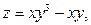 где
где 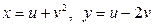 . Найти
. Найти 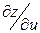 и
и 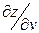 .
.
4. 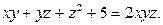 Найти
Найти 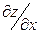 и
и 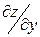 .
.
5. Исследовать на экстремум функцию 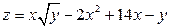 .
.
6. Составить уравнения касательной плоскости и нормали к поверхности: 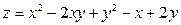 в точке
в точке 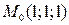 .
.








