При этом полный дифференциал первого порядка обладает свойством инвариантности, то есть формула его нахождения не зависит от того являются ли аргументы функции независимыми переменными или функциями.
Так же как и производные дифференциалы могут быть порядка выше первого.
Дифференциалом второго порядка функции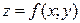 
называется дифференциал от дифференциала первого порядка: 
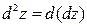. Аналогично: 
; 
; … ; 
.
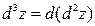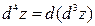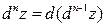Если аргументы функции 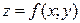являются независимыми переменными, то дифференциал второго порядка определяется по формуле: 
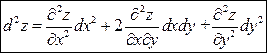(3) .
Приведенная формула напоминает формулу квадрата суммы двух слагаемых и формально может быть записана в виде: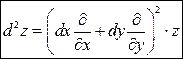 
.
Эта формальная схожесть сохраняется и для дифференциалов порядка выше второго. Поэтому общая формула дифференциалов высших порядков записывается в формальном виде:
.
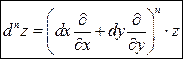Следует отметить, что полные дифференциалы порядка выше первого не обладают свойством инвариантности и имеют более сложный вид, если аргументы функции так же являются функциями.
Пример 1. Найти полный дифференциал функции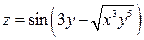 
.
1. Найдем частные производные первого порядка:
.
.
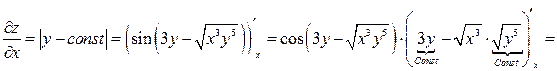
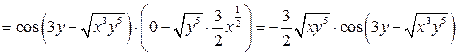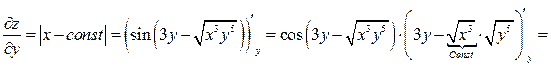
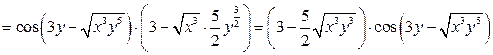2. Воспользуемся формулой (1) и запишем полный дифференциал функции: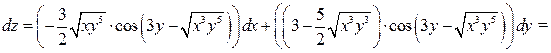 
.
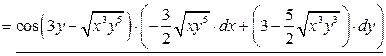Пример 2. Найти полный дифференциал функции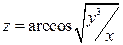 
.
1. Найдем частные производные первого порядка: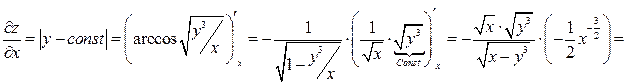 
. 
.
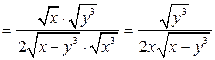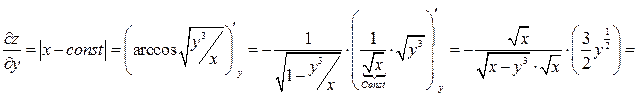
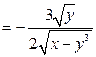2. Воспользуемся формулой (1) и запишем полный дифференциал функции:
.
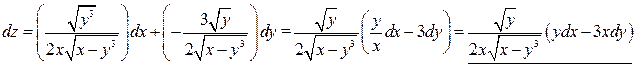Пример 3. Найти полный дифференциал функции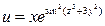 
.
1. Найдем частные производные первого порядка:
.
.
.
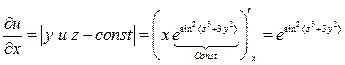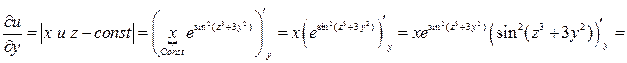
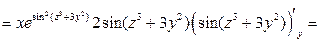
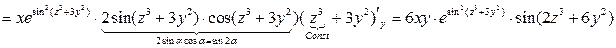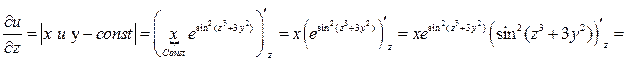
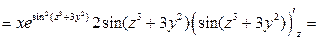
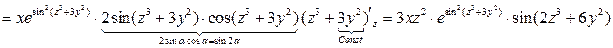2. Воспользуемся формулой (2) и запишем полный дифференциал функции:
.
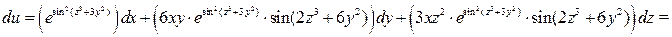
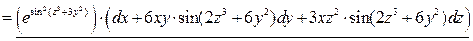Пример 4. Найти дифференциал второго порядка функции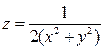 
.
Перепишем функцию в виде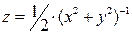 
.
1. Найдем частные производные первого порядка:
.
.
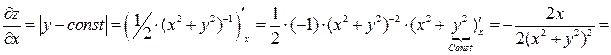
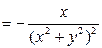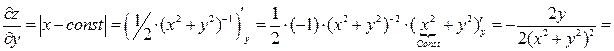
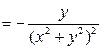2. Найдем три разные производные второго порядка:
.
.
.
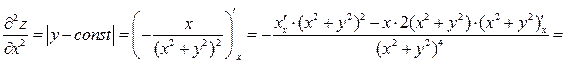
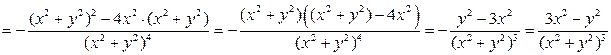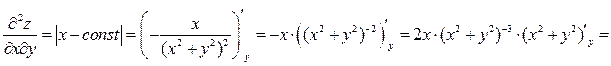
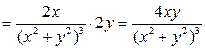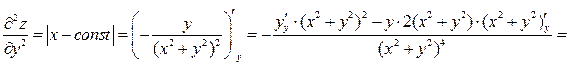
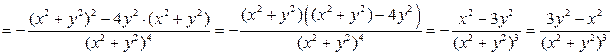2. Воспользуемся формулой (3) и запишем дифференциал функции второго порядка:
.
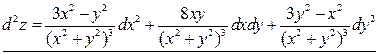2.8. Применение полного дифференциала.
Одним из случаев применения полного дифференциала является его использование для нахождения погрешностей величин, зависящих от нескольких факторов. Пусть дана функция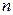 
- переменных: 
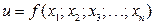. При этом, если при определении величин 
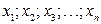, допущены погрешности 
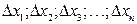, то сама величина 
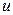так же будет найдена с погрешностью, равной приращению функции: 
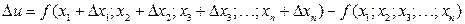. При малых значениях погрешностей 
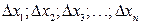приращение функции приблизительно равно ее дифференциалу: 
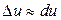. Поэтому: 
.
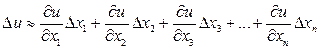Значения погрешностей могут быть как больше нуля, так и меньше. Значения частных производных тоже могут иметь разные знаки. Поэтому, если перейти в полученном выражении к модулям, то будет получена максимальная величина погрешности, которая называется максимальной абсолютной погрешностью величины 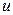и обозначается 
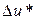. Таким образом, максимальная абсолютная погрешность величины может быть найдена по формуле:
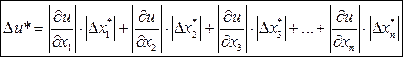(*), где 
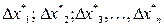- модули максимально возможных погрешностей величин 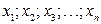. Относительной погрешностью называется отношение абсолютной погрешности к модулю номинального значения функции, то есть: 
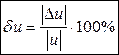. Обычно относительные погрешности измеряются в процентах.
Максимальной относительной погрешностью называется отношение максимальной абсолютной погрешности к модулю номинального значения функции, то есть: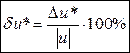 
(**).
Пример. Прямоугольный треугольник должен имеет катет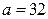 
и гипотенузу 
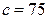. При построении катета допустима погрешность 
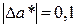, а при построении гипотенузы 
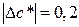. Каковы максимальные абсолютная и относительная погрешности угла 
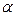, получаемые при таких погрешностях в построении.
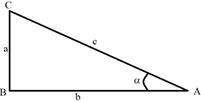Выразим угол 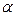, как функцию катета 
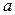и гипотенузы 
:
.
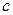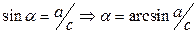Тогда номинальное значение угла равно: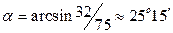 
.
Найдем абсолютные величины частных производных:
.
.
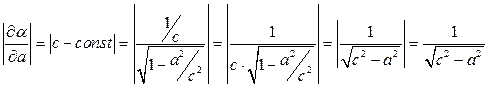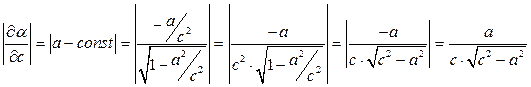Тогда по формуле (*) максимальная абсолютная погрешность будет равна:
.
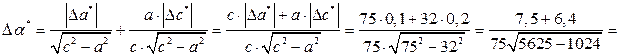
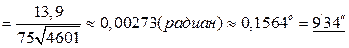Следовательно, значения угла 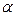при таких построениях, будут лежать в пределах: 
.
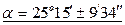Максимальная относительная погрешность:
.
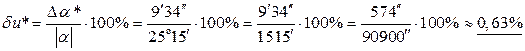2.9. Задание №7 на практические занятия и самостоятельную работу.
Решить самостоятельно на занятии: Б.П.Демидович «Задачи и упражнения по математическому анализу». №1806, 1809, 1811, 1813; 1835, 1837, 1846; 1892, 1893,1894, 1896, 1900; 1916; 1853, 1854. В задачнике Демидовича Б.П. есть краткая теория и разобранные примеры. Ответы в конце задачника.
Решить дома: Г.Н.Берман «Сборник задач по курсу математического анализа». №3042, 3044, 3050, 3064; 3104, 3105, 3109; 3184, 3189, 3192, 3194, 3193; 3220, 3222, 3224; 3118, 3122. Ответы в конце задачника.