Частные производные второго и более высоких порядков, взятые по разным переменным, называются смешанными.
Теорема. Две смешанные производные от одной и той же функции, отличающиеся лишь порядком
дифференцирования, равны между собой при условии их непрерывности.
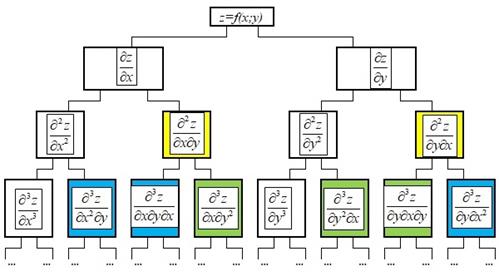Схема нахождения частных производных для функции двух переменных:
Равные смешанные производные выделены одинаковым цветом.
Для функции трех переменных схема будет похожей, но от каждой частной производной предыдущего порядка будет находиться по три частных производных следующего порядка.
Пример 1. Найти частные дифференциалы первого порядка и все частные производные второго порядка от функции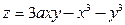 
, где 
.
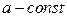Найдем частные производные первого порядка:
.
.
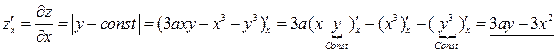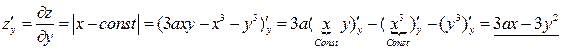Тогда частные дифференциалы первого порядка будут равны:
. 
.
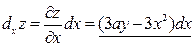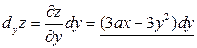Найдем частные производные второго порядка, продифференцировав найденные производные.
.
.
.
.
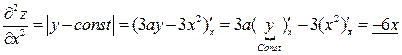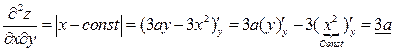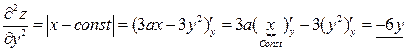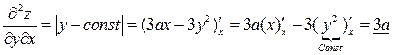Пример 2. Найти все частные производные второго порядка от функции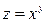 
.
Найдем частные производные первого порядка:
. 
.
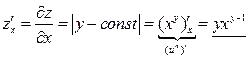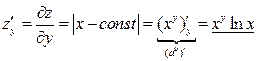Найдем частные производные второго порядка, продифференцировав найденные производные.
.
.
.
.
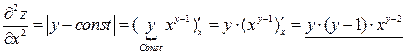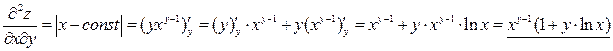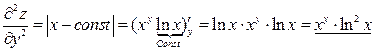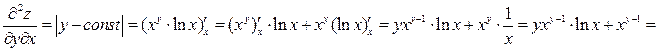
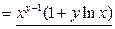Пример 3. Доказать равенство частных производных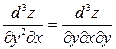 
функции 
.
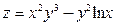Найдем необходимую частную производную первого порядка:
.
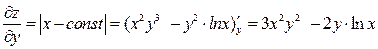Найдем необходимые частные производные второго порядка:
.
.
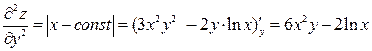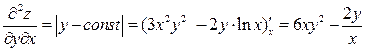Найдем необходимые частные производные третьего порядка:
.
.
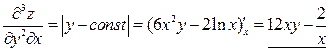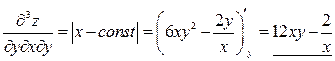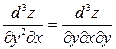, что и требовалось доказать.
2.7.Полное приращение и полный дифференциал функций нескольких переменных. Дифференциалы высших порядков.
Полное приращение - это приращение, которое получает функция при одновременном изменении всех ее аргументов. Так для функции двух переменных оно равно:
.
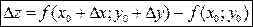Геометрически полное приращение такой функции равно изменению ее аппликаты при переходе из точки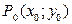 
в точку 
.
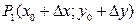Полным дифференциалом функции двух независимых переменных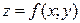 
называется главная часть полного приращения функции, линейная относительно приращений ее независимых переменных 
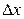и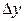 
.
Теорема. Полный дифференциал функции двух независимых переменных равен сумме произведений частных производных функции на дифференциалы соответствующих переменных (сумме частных дифференциалов функции). То есть: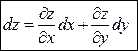 
(1) или 
.
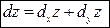Если функция имеет в некоторой точке полный дифференциал, то она называется в этой точке дифференцируемой.
Все сказанное справедливо и для функций большего числа переменных. Так для функции трех переменных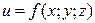 
формула (1) примет вид: 
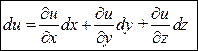(2) .