Разность вида называется частным приращением по функции в точке и обозначается так: , то есть: .
Лекция 7.
2.5. Частные приращения, производные и дифференциалы.
Рассмотрим функцию двух переменных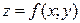 
. Зафиксируем один из ее аргументов, положив, например, 
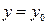. Тогда функция 
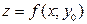станет функцией только одного аргумента 
.
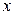Разность вида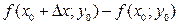 
называется частным приращением по 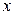функции 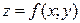в точке 
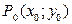и обозначается так: 
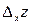, то есть: 
.
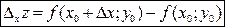Аналогично определяется и частное приращение по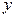 
: 
.
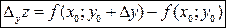В общем случае для функции любого числа аргументов частное приращение - это изменение функции, вызванное изменением лишь одного из ее аргументов.
Так как функция 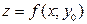является функцией только одного аргумента- 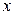, то для нее можно найти производную по : 
.
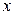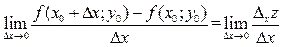Эта производная называется частной производной функции 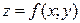по .
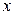Аналогично определяется и частная производная по :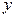 
.
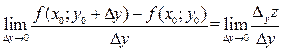Частные производные обычно обозначаются одним из следующих способов.
Частная производная по :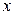 
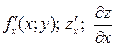. Частная производная по : 
.
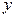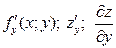Таким образом: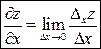 
и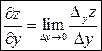 
.
Аналогично вводятся понятия частных производных функций большего числа аргументов.
Частная производная функции нескольких переменных - это производная, найденная по одному из ее аргументов при условии, что другие аргументы считаются константами.
Обозначаются такие производные так же.
Частные производные обладают всеми свойствами простых производных и находятся по тем же правилам.
Частным дифференциалом по 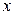функции 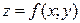называется главная часть частного приращения 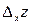, пропорциональная приращению 
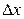независимой переменной 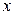. (См. лекцию 6 раздел 3.13 «Дифференциал функции», семестр 1).
При этом дифференциалы независимых переменных равны их приращениям: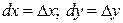 
.
Так же, как и для функции одной переменной, доказывается, что, если функция 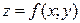имеет частный дифференциал по 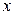, то она имеет и частную производную 
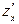. Обратное утверждение так же верно. При этом: 
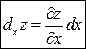и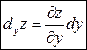 
.
Таким образом, частный дифференциал функции нескольких переменных равен произведению соответствующей частной производной на дифференциал этой переменной (справедливо для любого числа аргументов).
2.6. Частные производные высших порядков.
Так как частные производные являются функциями тех же переменных, что и дифференцируемые функции, то они в свою очередь так же могут иметь частные производные, которые называются частными производными второго порядка.
Аналогично вводятся понятия частных производных третьего, четвертого и более высоких порядков.
Так функция двух переменных 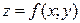имеет две частные производные первого порядка, четыре второго, восемь третьего и т.д.
Функция трех переменных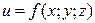 
переменных имеет три частные производные первого порядка, девять второго, двадцать семь третьего и т.д.