Размерность параметров уравнения Дарси в разных системах единиц
Таблица 1.2
| Параметры уравнения | Размерность | ||
| СИ | СГС | НПГ | |
| Объемный дебит, Q | м3 / с | см3 / с | см3 / с |
| Площадь поперечного сечения фильтра, F | м2 | см2 | см2 |
| Длина фильтра, L | м | см | см |
| Перепад давления, ∆P | Па | дн / см2 | атм |
| Вязкость жидкости, µ | Па · с | дн · с / см2 | спз (сантипуаз) |
В системе СИ коэффициент проницаемости измеряется в м2; в системе СГС [kпр] = см2; в системе НПГ (нефтепромысловой геологии) [kпр] = Д (Дарси).
1 Дарси = 1,02×10-8 см2 = 1,02 · 10-12 м2 » 1 мкм2.
Проницаемостью в 1 м2 называется проницаемость пористой среды при фильтрации через образец площадью 1 м2 длиной 1 м и при перепаде давления 1 Па, при которой расход жидкости вязкостью 1 Па×с составляет 1 м3.
Пористая среда имеет проницаемость 1 Дарси, если при однофазной фильтрации жидкости вязкостью 1 спз (спуаз) при ламинарном режиме фильтрации через сечение образца площадью 1 см2 и перепаде давления 1 атм., расход жидкости на 1 см длины породы составляет 1 см3/сек.
Физический смысл размерности проницаемости – это площадь сечения каналов пористой среды, через которые идет фильтрация.
Существует несколько типов каналов:
- субкапиллярные;
- капиллярные;
- трещины;
- разрывы.
Приведённые выше уравнения справедливы при условии движения несжимаемой жидкости по линейному закону Дарси.
В случае фильтрации газа это условие не выполняется. При перепаде давления объём газа изменяется, и оценивается по закону Бойля-Мариотта:
При Т = const, P·V = const (1.10)
При линейной фильтрации газа оценивается средняя скорость фильтрации (Vср):
Vcр· Pср = Vо ·Pо = V1· P1 = V2 · P2, (1.11)
Pср = (P1 + P2) / 2, (1.12)
Vcр = Vо·Pо / Pср = 2·Vо·Pо / (P1 + P2). (1.13)
Тогда, средний объёмный расход газа будет равен:
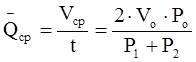. (1.14)
Отсюда уравнение коэффициента проницаемости для газа:
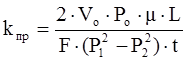. (1.15)
1.3.2. Радиальная фильтрация нефти и газа в пористой среде
Процесс притока пластовых флюидов из пласта в скважину описывается моделью радиальной фильтрации. В этом случае образец породы представляется в виде цилиндрического кольца с проводящими каналами в осевом направлении (рис. 1.7).
 |
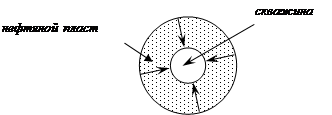Рис. 1.7. Схема радиального притока жидкости в скважину
Площадь боковой поверхности цилиндра: F=2prh, таким образом уравнение Дарси для радиальной фильтрации будет иметь следующий вид:
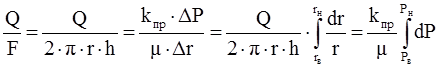. (1.16)
Отсюда, дебит при радиальной фильтрации жидкости:
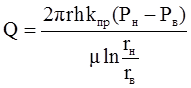. (1.17)
Таким образом, коэффициент проницаемости при радиальной фильтрации:
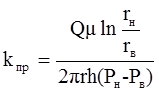. (1.18)
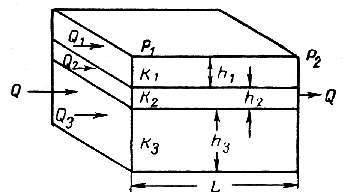
1.3.3. Оценка проницаемости пласта, состоящего из нескольких пропластков различной проницаемости
Пласт состоит, как правило, из отдельных пропластков, поэтому общая проницаемость пласта (kпр) оценивается с учетом проницаемости пропластков и направления фильтрации.
