Химическая кинетика. Катализ

Дата: 2025-05-01; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Скорость химической реакции

Любой процесс, любой переход системы из одного состояния в другое протекает во времени. Раздел химии, рассматривающий скорость и механизмы реакций, называется химической кинетикой.

Скорость химической реакции показывает число актов химического взаимодействия, приводящих к образованию продукта реакции в единицу времени в единице реакционного пространства. Измеряется скорость изменением концентрации реагирующих веществ в единицу времени.

Пусть за промежуток времени от t₁ до t₂ концентрация некоторого реагирующего вещества уменьшилась с С₁ до С₂. Тогда скорость реакции за данный измеримый промежуток времени называется средней скоростью реакции и выражается уравнением:

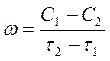(1)

Поскольку концентрация исходного вещества во времени убывает, т.е. C₂ < C₁ и (C₂ – C₁) < 0, а скорость не может быть отрицательной величиной, в выражении для скорости ставится знак минус. Если же скорость измеряется по увеличению концентрации продукта реакций, то в выражении (1) ставится знак плюс. В общем случае

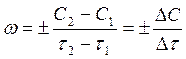(2)

Чем меньше промежуток времени Dt, тем ближе средняя скорость к истинной. За бесконечно малый промежуток времени Dt концентрация изменяется на бесконечно малое значение DC.

Следовательно, для истинной скорости реакций справедливо уравнение:

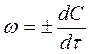(3)

Таким образом, истинная скорость реакции выражается производной концентрации данного вещества во времени.

Отметим, что определение скорости реакции как изменения концентраций веществ в единицу времени справедливо при условии постоянства реакционного пространства, т.к. в противном случае (например, в газофазных реакциях с 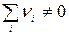) изменение концентраций будет происходить не только за счет реакции, но и вследствие изменения реакционного пространства. Так, в реакции синтеза аммиака:N ₂ +3 H ₂ =2 NH ₃ уменьшение концентраций простых газов будет значительно ниже, а увеличение концентрации аммиака – значительно выше, чем это обусловлено собственно химическим превращением. Поэтому надежнее считать скоростью реакции изменение количеств веществ в единицу времени в единице реакционного пространства:

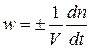(4)

Если V = const, то его можно ввести под знак дифференциала:

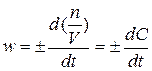(5)

Следует также отметить, что в определении скорости реакции необходим учет стехиометрии. Так, в реакции синтеза аммиака водород расходуется втрое быстрее, а аммиак образуется вдвое быстрее, чем расходуется азот. Поэтому для унифицирования полезно все выражения относить на единицу мольного количества вещества:

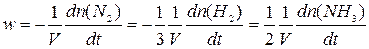(6)

Скорость процесса можно контролировать не только по изменению концентрации реагентов, но и по какому-либо свойству системы, изменяющемуся пропорционально концентрации (показатель преломления, электропроводность и т.п.). Если процесс протекает достаточно медленно, то через определенные промежутки времени отбирают пробы и определяют в них содержание вещества, по которому ведут определение скорости. Реакции, протекающие с большой скоростью, останавливают резким охлаждением (замораживают). Учитывая, что скорость реакции очень чувствительна к изменению температуры, реагирующую смесь обычно помещают в термостат.

Скорость различных реакций колеблется в огромных пределах. Самые медленные процессы – геохимические: они растягиваются на тысячелетия; самые быстрые – взрывные, протекающие за ничтожные доли секунды. Длительность обычных процессов измеряется часами, минутами, секундами.

Основными факторами, влияющими на скорость, являются: концентрация реагентов (давление – для реакций с участием газов), температура и наличие катализаторов.

Взаимодействие между молекулами реагентов может происходить только при их контакте, поэтому, чем чаще столкновения между молекулами, тем быстрее идет процесс. Поскольку число столкновений зависит от концентрации, то с ее ростом скорость реакции тоже должна возрастать.

Так для реакции А₂ + В₂ = 2АВ

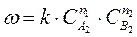(7)

Скорость реакции пропорциональна концентрациям реагирующих веществ, взятых в определенных степенях.

Коэффициент пропорциональности k называется константой скорости. k = w, когда концентрации каждого вещества равны 1, поэтому константу скорости еще называют «удельной скоростью».

Обычно кинетику реакций характеризуют именно величиной константы скорости. Она не зависит от времени реакции, а определяется лишь природой реагентов, температурой и катализатором. Скорость реакции по мере уменьшения концентрации исходных веществ убывает.

Показатели степени n₁ и n₂ называются порядками реакции по компонентам. Сумма показателей степени в уравнении основного закона кинетики (основное кинетическое уравнение) (7) называется общим порядком реакции. Это может быть любое число, положительное и отрицательное, целое и дробное. Существуют специальные методы определения порядка реакции.

В простейшем случае, когда реакция идет в одну стадию (элементарная реакция, почти никогда не встречается), порядки по компонентам совпадают со стехиометрическими коэффициентами в уравнении реакции. Например, для реакции 2А + В = А₂В

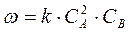(8)

Эту зависимость, получившую название закона действующих масс, впервые установили скандинавские ученые Гульдберг и Вааге (1867 г.).

При повышении температуры скорость реакции увеличивается. Это объясняется тем, что возрастает доля так называемых «активных молекул», т.е. молекул с повышенным запасом энергии по сравнению со средней величиной энергии молекул. При столкновении активных молекул происходит химическое взаимодействие.

Считается, что для большинства реакций повышение температуры на 10°С вызывает увеличение скорости в 2-4 раза (правило Вант-Гоффа):

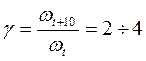(9)

Величина g называется температурным коэффициентом реакции.

При повышении температуры на любое число градусов:

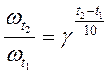. (10)

Температурный коэффициент g может быть найден из коэффициента регрессии, по методу наименьших квадратов (линейная регрессия; можно порекомендовать программу Линия в оболочке Excel, автор Г.М. Можаев); обрабатываемую зависимость линеаризуют; после линеаризации уравнения Вант-Гоффа получается линейная зависимость :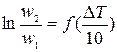

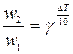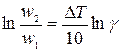; (11)

Диапазон температур – любой, желательно – не очень широкий. Достаточно получить результаты для четырех температур, чтобы иметь для обработки 6 точек. Разница температур – произвольная (и не обязательно кратная 10).

Следует заметить, что оценка температурной зависимости скорости реакции по правилу Вант-Гоффа весьма приближенна, и температурный коэффициент укладывается в интервал от 2 до 4 лишь для реакций с аррениусовой энергией активации Е_А порядка 50-100 кДж/моль. Так, скорость изомеризации циклопропана в пропилен (Е_А=272,8 кДж/моль) при повышении температуры на 10^о увеличивается более чем в 40 раз, а для получения нитрозилбромида из брома и окиси азота (Е_А=5,44 кДж/моль) – не в разы, а всего на несколько процентов. Соответственно, вычисленный температурный коэффициент позволяет оценить аррениусову энергию активации.

Более точно и надежно температурная зависимость константы скорости (а, следовательно – и самой скорости реакции, при неизменности концентрационного фактора) оценивается по уравнению Аррениуса:

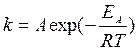(12)

Уравнение также легко линеаризуется:

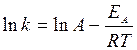(13)

При обработке (регрессионный анализ) этой линейной зависимости 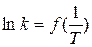, можно найти аррениусовы параметры – энергию активации Е_А (из коэффициента регрессии) и предэкспоненциальный множитель А (из свободного члена).

В сущности, главной причиной увеличения скорости реакции с повышением температуры является увеличение доли реакционноспособных частиц. И по своему физическому содержанию предэкспоненциальный множитель А представляет собой константу скорости при достаточно высокой температуре, когда энергетический активационный барьер отсутствует или незначим, все реагирующие частицы реакционноспособны, и любое их столкновение химически активно.

Что касается энергии активации, то в теоретическом смысле – это минимальная энергия реакционноспособных частиц. Следует, однако, иметь в виду, что теоретический смысл энергии активации как высоты энергетического активационного барьера для реагирующих частиц совершенно исчезает, если скорость реакции с повышением температуры не увеличивается, а уменьшается. Такая ситуация довольно редко, но, тем не менее, встречается. Достаточно привести пример практически очень важной реакции окисления окиси азота кислородом:

2 NO + O ₂ = 2 NO ₂

Скорость этой реакции с повышением температуры уменьшается (этому есть вполне разумное теоретическое толкование), и экспериментальная оценка аррениусовой энергии активации дает отрицательное значение: Е_А=-4,7 кДж/моль. Поэтому достаточно определить аррениусову энергию активации просто как численный параметр, отражающий меру температурной зависимости константы скорости.

Не следует однозначно утверждать, что более высокое значение аррениусовой энергии активации всегда соответствует более низкое значение константы скорости. Здесь надо учитывать рассматриваемую область температур. Две сравниваемые реакции с разными аррениусовыми энергиями активации будут характеризоваться разным наклоном линий 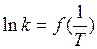и при некоторой температуре эти линии пересекутся. Легко видеть, что ниже этой температуры действительно быстрее протекает реакция с более низкой аррениусовой энергией активации. Но выше этой температуры – ситуация обратная: быстрее будет протекать реакция с более высокой аррениусовой энергией активации. Напрашивается косвенная аналогия с движущими силами в химической термодинамике. Здесь при невысоких температурах определяющим будет энергетический фактор, выделение энергии и снижение энтропии, за счет образования связей, структурирования и упорядочения, тогда как при высоких – энтропийный. В теоретической кинетике, наряду с понятием энергия активации, существует понятие энтропия активации, которая также входит в уравнение Аррениуса в экспоненциальной форме в составе предэкспоненциального множителя. Для ряда однотипных реакций отмечен компенсационный эффект: большее значение энергии активации, более высокий энергетический активационный барьер компенсируется более высоким значением предэкспоненциального множителя, большей энтропией активации:

PhCH ₂ I + EtO ^- = PhCH ₂ OEt + I ^-; E_A=83,3 кДж/моль; А=1,5∙10¹³ см³/(моль∙с)

PrI + EtO ^- = PrOEt + I ^-; E_A=94,2 кДж/моль; А=3,5∙10¹⁴ см³/(моль∙с)

Процессы, в которых реагирующие вещества находятся в различных агрегатных состояниях, называются гетерогенными.

В общем случае скорость реакции в гетерогенных процессах пропорциональна площади поверхности соприкосновения реагирующих веществ. По этой причине порошки значительно быстрее окисляются кислородом, чем массивные куски вещества; мелко раздробленный мрамор быстрее реагирует с соляной кислотой, чем его крупные куски.

Экспериментальная часть