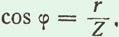Тема: Электрическая цепь переменного тока с активным и индуктивным сопротивлением
ОП.02. ЭЛЕКТРОТЕХНИКА
25.03.2022
Лекция № 18
Тема: Электрическая цепь переменного тока с активным и индуктивным сопротивлением
Задание:
1. Изучить и законспектировать новый материал
2. Зарисовать необходимые графики функций
3. Просмотреть обучающий ролик по ссылке в конце лекции для закрепления пройденного материала.
4. Фотоотчет конспекта выслать на адрес до следующего занятия : elena.lazarenko712@gmail.com или https://vk.com/id16032478
Говоря о переменном токе, часто оперируют такими терминами как «фаза», «фазовый угол», «сдвиг фаз». Обычно это касается синусоидального переменного или пульсирующего тока (полученного путем выпрямления синусоидального тока).
Поскольку периодическое изменение ЭДС в сети или тока в цепи — это гармонический колебательный процесс, то и функция, описывающая данный процесс, - гармоническая, то есть синус или косинус, в зависимости от начального состояния колебательной системы.
Аргументом функции в данном случае является как раз фаза, то есть положение колеблющейся величины (тока или напряжения) в каждый рассматриваемый момент времени относительно момента начала колебаний. А сама функция принимает значение колеблющейся величины, в этот же момент времени.
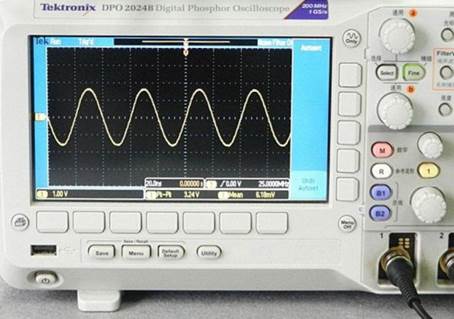
Рис.1. Графичесий вид синусоидального тока на осциллографе
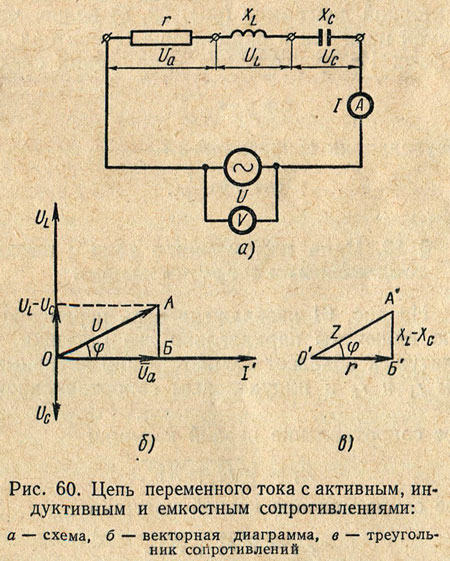
На рис. 60, а изображена цепь переменного тока, в которую включены последовательно активное сопротивление r, индуктивность L, обладающая индуктивным сопротивлением ХL и емкость С, обладающая емкостным сопротивлением Хc.
Под действием переменного напряжения в этой цепи протекает переменный ток.
Выясним, чему равно общее напряжение на зажимах цепи. Построим векторную диаграмму тока и напряжений для рассматриваемой цепи (рис. 60, б). Так как сопротивления соединены последовательно, то в них протекает одинаковый ток. Отложим по горизонтали в выбранном масштабе вектор тока I. В цепи с активным сопротивлением ток и напряжение совпадают по фазе, поэтому вектор напряжения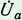 
откладываем по вектору тока.
Напряжение на индуктивности опережает ток на угол φ = 90°. Поэтому вектор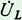 
откладываем вверх под углом 90° к вектору тока.
В цепи с емкостью, наоборот, напряжение отстает от тока на угол φ = 90°. Поэтому вектор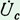 
откладываем на диаграмме вниз под углом 90° к вектору тока.
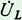Для определения общего напряжения, приложенного к зажимам цепи, сложим векторы и 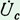. Для этого отнимем от большего вектора 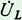вектор 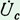и получим вектор 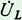— 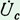, выражающий векторную сумму этих двух напряжений. Теперь сложим векторы ( 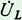— 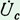) и 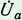. Суммой этих векторов будет диагональ параллелограмма — вектор 
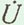, изображающий общее напряжение на зажимах цепи.
На основании теоремы Пифагора из треугольника напряжений АОБ следует, что
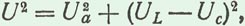
отсюда общее напряжение
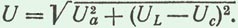
(69)
Определим полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I, выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А′О′Б′ (рис. 59, в). Его сторонами являются сопротивления r, (ХL — Хc) и полное сопротивление цепи Z. Пользуясь теоремой Пифагора, можно написать, что
Z 2 =r2 + (ХL — Хc)2.
Отсюда полное сопротивление цепи
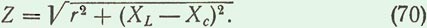
Формула (70) может применяться и в частных случаях, когда ХL = 0 или Хc = 0.
Силу тока в цепи с активным, индуктивным и емкостным сопротивлениями определяют по закону Ома:
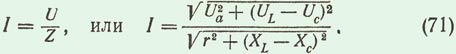
На векторной диаграмме (рис. 59, б) видно, что в рассматриваемой цепи ток и напряжение генератора не совпадают по фазе. Из треугольника напряжений следует, что
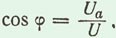
Из треугольника сопротивлений
