Формулы решения неполных квадратных
ТРИГОНОМЕТРИЯ
Формулы решения простейших
тригонометрических уравнений
Таблица 1.
| sin x | cos x | tg x | ctg x | |
| 0 | x = 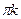
| x = 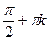
| x = 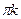
| x = 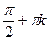
|
| 1 | x = 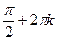
| x = 2 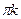
| x = 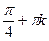
| x = 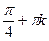
|
| –1 | x = – 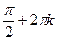
| x = 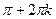
| x = – 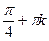
| x = – 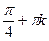
|
k  z z
| k  z z
| k  z z
| k  z z
|
Примеры
| 1. sin2x · sinx = 0 | 2. cos23x – 5 cos3x = 0 cos3x (cos3x – 5) = 0 | ||
sin 2x = 0
2x = 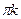 x =
x = 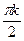
| sin x = 0
x = 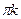
| cos3x = 0
3x = 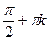 x =
x = 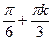
| cos3x – 5= 0 cos3x = 5 нет решений |
| Ответ: | Ответ: | ||
Общие формулы решения
тригонометрических уравнений
Таблица 2.
sinx = 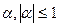
| cosx = 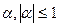
| tgx = 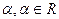
| ctgx = 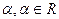
|
x = (-1)кarcsina+Пк
k  z z
|
x = 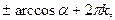 k
k  z z
|
x = 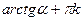 ,
k ,
k  z z
|
x = 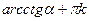 ,
k ,
k  z z
|
Примеры
| 1. 2sin3x = –1 | 2. 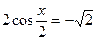
|
sin 3x = 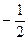
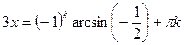
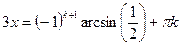
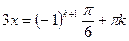
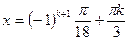 , k , k  z z
| 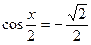
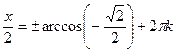
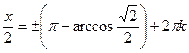
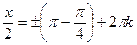
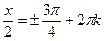 x =
x = 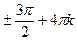 , k , k  z z
|
Формулы решения неполных квадратных
тригонометрических уравнений
Таблица 3.
sin2x = 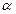
| cos2x = 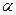
| tg2x = 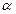
| ctg2x = 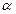
|
x = 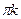 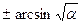 k
k  z z
|
x = пк±arccos 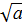 k
k  z z
|
x = 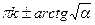 ,
k ,
k  z z
|
x = 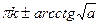 ,
k ,
k  z z
|
Примеры
1 . sin2x = 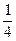
| 2. tg2x =3 |
x = 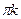 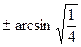 x =
x = 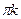 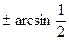 x =
x = 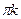 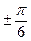 , k , k  z z
| x = 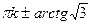 x =
x = 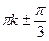 , k , k  z z
|
Однородные тригонометрические уравнения
| Однородное уравнение первой степени Acosx + Bsinx = 0 | Однородное уравнение второй степени Asin2x + Bsinx cosx + Ccos2x= 0 |
Решаем путём деления обеих частей уравнения на sinx или cosx.
(x 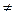  или x или x 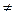 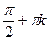 ), k ), k  z z
| Решаем путём деления обеих частей уравнения на sin2x или cos2 x.
(x 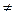 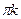 или x или x 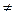 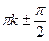 ), k ), k  z z
|
Примеры
| 1. 5sinx + 6cosx = 0 | 2. 2cos2x + 5sinxcosx + 3sin2x = 0 | |
Делим обе части на cosx 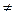 0
5tgx + 6 = 0
5tgx = –6
tgx = – 0
5tgx + 6 = 0
5tgx = –6
tgx = – 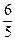 x =
x = 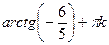 x =
x = 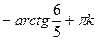 , k , k  z z
| Делим обе части на cos2x 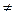 0
3tg2 x + 5tg x + 2 = 0
Пусть tgx = t, тогда 3t2 + 5t + 2 = 0
D = 25 – 24 = 1 0
3tg2 x + 5tg x + 2 = 0
Пусть tgx = t, тогда 3t2 + 5t + 2 = 0
D = 25 – 24 = 1
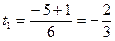 ; ;
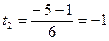 tgx =
tgx = 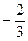 ; tgx = –1
x = ; tgx = –1
x = 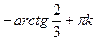 x = x = 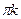 + arctg(-1)
k + arctg(-1)
k  z x = z x = 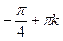 k k  z z
|
Неоднородные тригонометрические уравнения
A sinx + Bcosx = C
Решаем путём деления обеих частей уравнения на 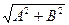 ; сводим левую часть уравнения к теоремам сложения.
; сводим левую часть уравнения к теоремам сложения.
Пример
sinx + cosx = 1
A = 1, B = 1 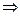
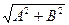 =
= 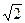
Делим обе части на 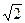
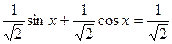
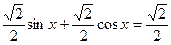
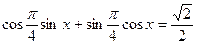
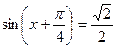
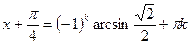
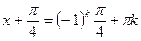
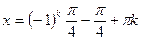 , k
, k  z
z
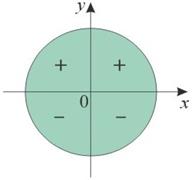
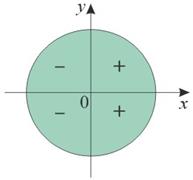
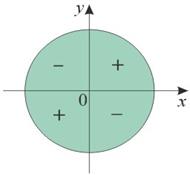
Знаки тригонометрических функций
| sinα | cosα | tgα, ctgα | ||
|
|
|
Пример:
Определить знак выражения 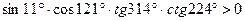 .
.
Чётность, нечётность тригонометрических функций
| Чётные | Нечётные | Общего вида | ||

| 
| 
| ||
| cos(–x) = cosx | sin(–x) = sinx tg(–x) = –tgx ctg(–x) = –ctgx arcsin(–x) = –arcsinx arctg(–x) = –arctgx |
arccos(–x) = 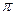 –arccosx
arcctg(–x) = –arccosx
arcctg(–x) = 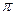 –arcctgx –arcctgx
|
Примеры :
1. sin(–30°) = –sin30° = – 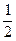
2. cos(–45°) = cos45° = 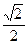
3. tg(–45°) = –tg45° = –1
4. arcsin 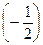 = –arcsin
= –arcsin 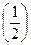 = –
= – 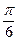
5. arcos 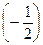 =
= 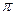 – arccos
– arccos 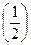 =
= 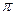 –
– 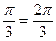 .
.
Периодичность тригонометрических функций
 |  |
sin( 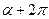 ) = sin ) = sin 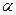 cos(
cos( 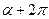 ) = cos ) = cos 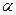
|
tg( 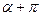 ) = tg ) = tg 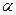 ctg(
ctg( 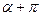 ) = ctg ) = ctg 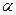
|
Примеры :
1. sin 390° = sin30° = 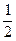
2. tg 240° = tg60° = 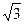
3. sin 1110° = sin 30° = 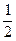
Соотношения между тригонометрическими
функциями одного аргумента
  sin2α + cos2α = 1 sin2α + cos2α = 1
|


| sin2α = 1 – cos2α | 1 + ctg2α = 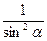
| cos2α = 1 – sin2α | 1 + tg2α = 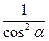
| |||

| 
| 
| 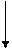
| |||
sinα = 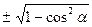
| sinα = 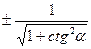
| cosα = 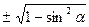
| cosα = 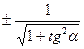
|
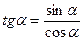
| 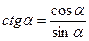
| |

| 
| |
| tgα ctg α = 1 | ||

| 
| |
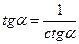
| 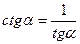
|
Примеры :
1. Упростить: 
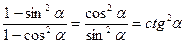
2. 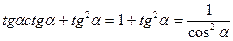
3. sinα = 0,6 α  II четверти.
II четверти.
Найти cosα, tgα, ctg α.
Решение:
1. 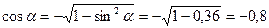
2. tgα = 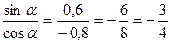
3. ctgα = 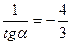 .
.
| Теоремы сложения | Формулы приведения | |
sin(α + β) = sinα cosβ + cosαsinβ
sin(α – β) = sinα cosβ – cosαsinβ
cos(α + β) = cosα cos β – sinαsinβ
cos(α – β) = cosαcosβ + sinαsinβ
tg(α + β) = 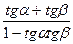 tg(α – β) =
tg(α – β) = 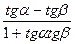 сtg(α + β) =
сtg(α + β) = 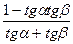 сtg(α – β) =
сtg(α – β) = 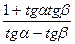
| 1. а) Для углов 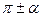 название исходной функции сохраняется.
б) Для углов название исходной функции сохраняется.
б) Для углов 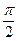 ± α; ± α; 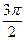 ± α название исходной функции меняется:
синус на косинус
косинус на синус
тангенс на котангенс
котангенс на тангенс.
2. Окончательный знак в выражении ставится тот, который имеет исходная функция (считают что α – угол первой четверти.) ± α название исходной функции меняется:
синус на косинус
косинус на синус
тангенс на котангенс
котангенс на тангенс.
2. Окончательный знак в выражении ставится тот, который имеет исходная функция (считают что α – угол первой четверти.)
|
Примеры :
Упростить:
| 1. sinαcos2α + cosαsin2α = sin(α+2α) = = sin3α 2. cos5αcosα + sin5αsinα = cos(5α – α) = cos4α | 1. sin135°=sin(90°+45°) = cos45°=
= 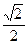 2. tg120°= tg(90°+ 30°) = -ctg 30° =
= -
2. tg120°= tg(90°+ 30°) = -ctg 30° =
= - 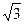
|
| Формулы двойного аргумента | Выражение sinα, cosα и tgα через тангенс половинного аргумента | Формулы понижения степени |
sin2α = 2sinαcosα
cos2α = cos2α – sin2α
tg2α = 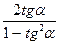 ctg2α =
ctg2α = 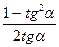
| sinα = 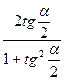 cosα =
cosα = 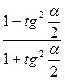 tgα =
tgα = 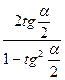
| 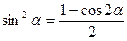
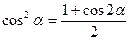 tg2 =
tg2 = 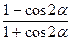
|
Примеры:
| 1. 4sinαcosα = 2sin2α 2. 16sin4α cos4α · cos8α = = 8sin8αcos8α = 4sin16α 3. cos28α – sin28α = = cos16α |
Вычислить:
1. 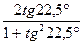 = sin45°=
= = sin45°=
= 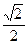 2.
2. 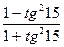 = cos30°= = cos30°= 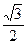
| 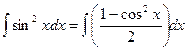 =
= =
= 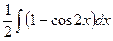 =
= =
= 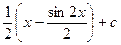 =
= =
= 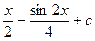
|
Преобразование произведений тригонометрических
функций в сумму и обратно
sinαcosβ = 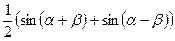 sinαsinβ =
sinαsinβ = 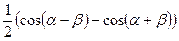 cosαcosβ =
cosαcosβ = 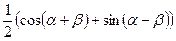 tgαtgβ =
tgαtgβ = 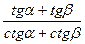 сtgαctgβ =
сtgαctgβ = 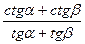
|
sinα + sinβ = 2sin 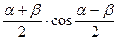 sinα – sinβ = 2sin
sinα – sinβ = 2sin 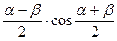 cosα + cosβ = 2cos
cosα + cosβ = 2cos 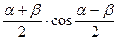 cosα – cosβ = –2sin
cosα – cosβ = –2sin 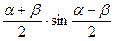 tgα + tgβ =
tgα + tgβ = 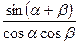 tgα – tgβ =
tgα – tgβ = 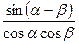 сtgα + ctgβ =
сtgα + ctgβ = 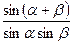 сtgα – ctgβ =
сtgα – ctgβ = 
|
Упростить:
sin5αcos3α = 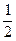 (sin8α + sin2α) =
= (sin8α + sin2α) =
= 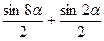 
| sin3x + sin5x = 0
2sin4xcos(–x) = 0
sin4xcosx = 0
sin4x =0 cosx = 0
4x = 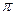 k x = k x = 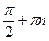 x =
x = 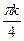 n n  z
k z
k  z z
|
Значения тригонометрических функций
для некоторых углов
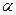
| 0°(0 рад) | 30° 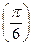
| 45° 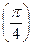
| 60° 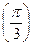
| 90° 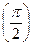
|
180° 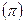
| 270° 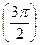
|
360° 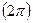
|
sin 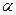
| 0 | 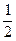
| 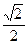
| 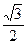
| 1 | 0 | –1 | 0 |
cos 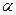
| 1 | 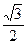
| 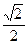
| 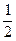
| 0 | –1 | 0 | 1 |
tg 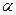
| 0 | 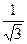
| 1 | 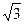
| – | 0 | – | 0 |
ctg 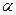
| – | 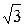
| 1 | 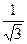
| 0 | – | 0 | – |
sec 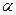
| 1 | 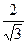
| 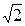
| 2 | – | –1 | – | 1 |
cosec 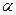
| – | 2 | 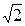
| 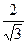
| 1 | – | –1 | – |








