2.2.2. Последовательность синтеза ФНЧ (ФВЧ) по характеристическим параметрам
Расчетные формулы получены из основных положений методики синтеза по характеристическим параметрам, приведенных в подразделе 2.2.1 данных методических указаний. В частности, формулы (27), (28) для определения значений элементов звена, получены из выражений (23), (24). При синтезе по характеристическим параметрам, последовательность расчетов для ФНЧ и ФВЧ следующая:
а) рассчитываются номиналы идеальных индуктивности и емкости Г- звена фильтра, по заданным в задании значениям сопротивлений нагрузки, генератора и значению граничной частоты полосы пропускания:
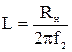 , (27)
, (27)
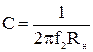 , (28)
, (28)
где 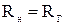 - значения сопротивлений нагрузки и генератора,
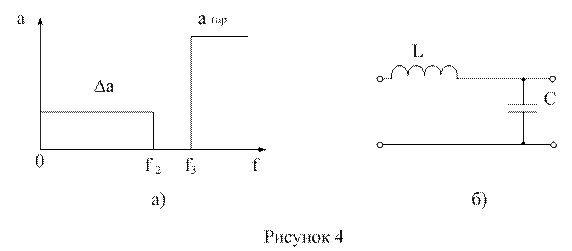
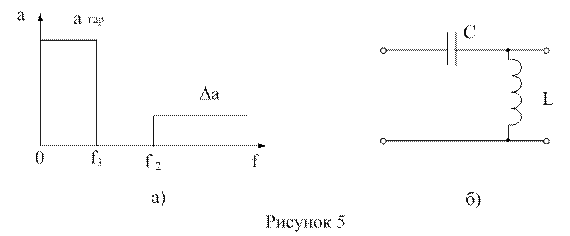
- значения сопротивлений нагрузки и генератора, 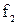 - значение граничной частоты полосы пропускания. График требований к ослаблению и схема Г – образного звена ФНЧ приведены на рисунках 4 а,б. На рисунках 5 а, б приведены требования к ослаблению и схема Г – образного звена ФВЧ.
- значение граничной частоты полосы пропускания. График требований к ослаблению и схема Г – образного звена ФНЧ приведены на рисунках 4 а,б. На рисунках 5 а, б приведены требования к ослаблению и схема Г – образного звена ФВЧ.
б) рассчитывается ослабление звена ( 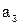 ) в децибеллах на граничной частоте полосы задерживания (
) в децибеллах на граничной частоте полосы задерживания ( 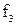 ), по заданному значению коэффициента прямоугольности (
), по заданному значению коэффициента прямоугольности ( 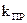 ). Для ФНЧ:
). Для ФНЧ:
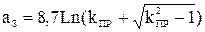 . (29)
. (29)
Для фильтра верхних частот:
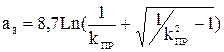 . (30)
. (30)
В расчетах по формулам (29), (30) - применяется натуральный логарифм;
в) рассчитывается количество звеньев ( 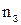 ) по заданному в задании значению гарантированного ослабления на границе полосы задерживания, в соответствии с формулой (26):
) по заданному в задании значению гарантированного ослабления на границе полосы задерживания, в соответствии с формулой (26):
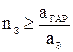 .
.
Значение 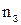 округляется до ближайшего большего целого значения;
округляется до ближайшего большего целого значения;
г) рассчитывается ослабление фильтра в децибеллах для нескольких значений частот в полосе задерживания (расчетное ослабление в полосе пропускания, без учета тепловых потерь, в этом методе считается равным нулю). Для фильтра нижних частот:
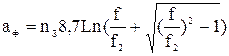 . (31)
. (31)
Для фильтра верхних частот:
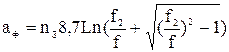 ; (32)
; (32)
д) анализируются тепловые потери ( 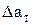 ). Для приближенного расчета тепловых потерь по ‘низкочастотному прототипу’, вначале определяются на частоте
). Для приближенного расчета тепловых потерь по ‘низкочастотному прототипу’, вначале определяются на частоте 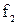 ‘резистивные’ сопротивления реальных катушек индуктивности (
‘резистивные’ сопротивления реальных катушек индуктивности ( 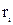 ), при самостоятельно выбранных значениях добротности (
), при самостоятельно выбранных значениях добротности ( 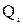 ). Катушки индуктивности, в дальнейшем, в схеме электрической принципиальной, будут введены вместо идеальных
). Катушки индуктивности, в дальнейшем, в схеме электрической принципиальной, будут введены вместо идеальных  индуктивностей (конденсаторы считаются более высокодобротными и их ‘резистивные’ потери не учитываются). Расчетные формулы:
индуктивностей (конденсаторы считаются более высокодобротными и их ‘резистивные’ потери не учитываются). Расчетные формулы:
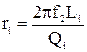 , (33)
, (33)
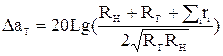 . (34)
. (34)
Ослабление фильтра в децибелах, с учетом тепловых потерь, определяется:
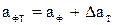 , (35)
, (35)
а модуль коэффициента передачи по напряжению ( 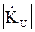 ), определяется из соотношения, связывающего его с ослаблением фильтра:
), определяется из соотношения, связывающего его с ослаблением фильтра:
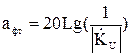 ; (36)
; (36)
е) по результатам расчетов по формулам (35), (36), строятся графики ослабления и модуля коэффициента передачи по напряжению, для ФНЧ или ФВЧ;
ж) по справочникам радиоэлементов выбираются ближайшие по номиналу к идеальным элементам стандартные конденсаторы и катушки индуктивности, для последующей разработки схемы электрической принципиальной и перечня элементов всей электрической цепи. В случае отсутствия стандартных катушек индуктивностей нужного номинала необходимо их разработать самостоятельно. На рисунке 6 показаны основные размеры простой цилиндрической катушки с однослойной намоткой, необходимые для ее расчета.
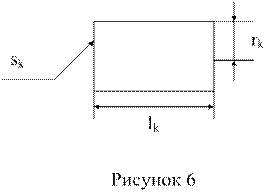
Число витков такой катушки с ферромагнитным сердечником (феррит, карбонильное железо), определяется из выражения:
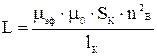 , (37)
, (37)
где 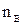 - число витков,
- число витков, 
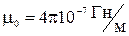 - абсолютная магнитная проницаемость,
- абсолютная магнитная проницаемость, 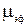 - относительная магнитная проницаемость материала сердечника,
- относительная магнитная проницаемость материала сердечника, 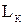 - длина катушки,
- длина катушки, 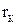 - радиус основания катушки,
- радиус основания катушки, 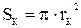 .
.
2.2.3. Последовательность синтеза ПФ (РФ) по характеристическим параметрам
На рисунках 7 а,б и 8 а,б приведены графики требований к ослаблению и простейшие Г- образные звенья, соответственно, для полосового и режекторного фильтров.
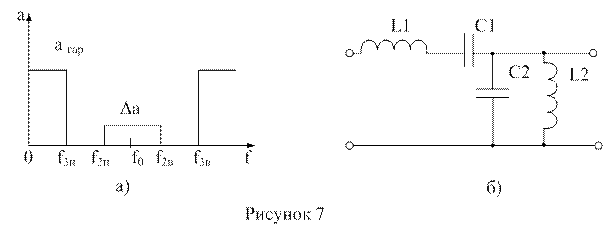
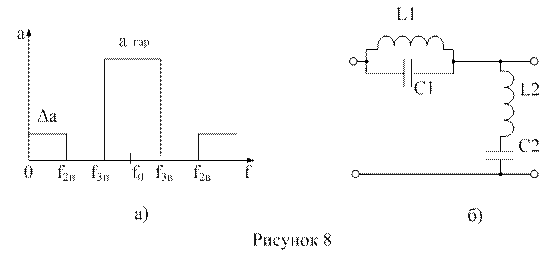
Синтез ПФ и РФ рекомендуется проводить, используя расчеты фильтров-прототипов с такой же полосой пропускания и задерживания. Для ПФ – прототипом является фильтр нижних частот, а для РФ – фильтр верхних частот. Методика синтеза следующая:
а) на первом этапе синтеза применяется частотное преобразование, при котором графические требования к ослаблению ПФ пересчитываются в требования к ослаблению ФНЧ, а графические требования к ослаблению РФ пересчитываются в требования к ослаблению ФВЧ:
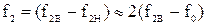 , (38)
, (38)
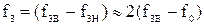 ; (39)
; (39)
б) по рассмотренной ранее методике синтеза ФНЧ и ФВЧ (пункты ‘а’ - ‘е’ подраздела 2.2.2) разрабатывается схема электрическая эквивалентная ФНЧ, для синтеза ПФ, или ФВЧ, для синтеза РФ. Для ФНЧ или ФВЧ строятся графики ослабления и коэффициента передачи по напряжению;
в) схема ФНЧ преобразуется в схему полосового фильтра – преобразованием продольных ветвей в последовательные колебательные контуры и поперечных ветвей в параллельные колебательные контуры, за счет подключения добавочных реактивных элементов. Схема ФВЧ преобразуется в схему режекторного фильтра - преобразованием продольных ветвей в параллельные колебательные контуры и поперечных ветвей в последовательные колебательные контуры, за счет подключения добавочных реактивных элементов. Добавочные реактивные элементы для каждой ветви ФНЧ (ФВЧ) определяются по значению заданной средней частоты полосового или режекторного фильтра ( 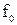 ) и рассчитанным значениям реактивных элементов ветвей ФНЧ (ФВЧ), используя известное выражение для резонансных контуров:
) и рассчитанным значениям реактивных элементов ветвей ФНЧ (ФВЧ), используя известное выражение для резонансных контуров:
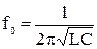 ; (40)
; (40)
г) для схем ПФ или РФ разрабатываются или выбираются по справочникам радиоэлементов конденсаторы и катушки индуктивности, по той же методике, которая рассматривалась ранее в подразделе 2.2.2 (пункт ‘ж’) данных методических указаний;
д) графики ослабления и коэффициента передачи по напряжению ФНЧ (ФВЧ) пересчитываются в графики ПФ (РФ), в соответствии с соотношениями между частотами этих фильтров. Например, для преобразования графиков ФНЧ к ПФ:
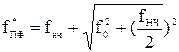 , (41)
, (41)
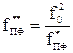 , (42)
, (42)
где 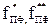 - частоты, соответственно, выше и ниже средней частоты полосового фильтра. По этим же формулам пересчитываются графики фильтра верхних частот в графики режекторного фильтра.
- частоты, соответственно, выше и ниже средней частоты полосового фильтра. По этим же формулам пересчитываются графики фильтра верхних частот в графики режекторного фильтра.
2.3. Методика синтеза фильтров по рабочим параметрам
2.3.1. Основные принципы синтеза по рабочим параметрам (полиномиального синтеза)
В данном методе синтеза также, как и при синтезе по характеристическим параметрам, задаются требования к типу проектируемого фильтра, активному сопротивлению нагрузки, ослаблению или коэффициенту передачи мощности в полосе пропускания и задерживания. Однако учитывается, что входное и выходное сопротивления фильтра изменяются в полосе пропускания. В этой связи, фильтр синтезируется в несогласованном режиме, то есть по рабочим параметрам, что в исходных данных отражается требованием 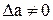 . Метод основан на обязательном расчете для любых типов фильтров низкочастотного фильтра – прототипа (фильтра нижних частот). В расчетах используется нормирование (
. Метод основан на обязательном расчете для любых типов фильтров низкочастотного фильтра – прототипа (фильтра нижних частот). В расчетах используется нормирование ( 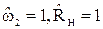 ) и частотные преобразования.
) и частотные преобразования.
Эквивалентная схема фильтра разрабатывается не из отдельных одинаковых звеньев, а сразу полностью, обычно в виде схемы ‘цепочной’ структуры. На рисунке 9 показан вид П – образной цепочной схемы фильтра нижних частот, а на рисунке 10 – вид Т – образной схемы такого же фильтра, с ненормированными элементами.
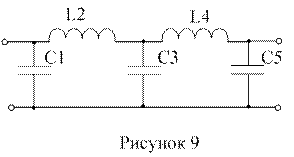
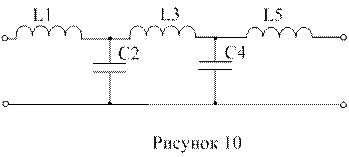
Основные этапы расчетов, на которых основан данный синтез, следующие:
а) аппроксимация - замена графических требований к коэффициенту передачи мощности аналитическим выражением, например, отношением полиномов по степеням 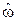 , что соответствует формулам частотных характеристик реальных реактивных фильтров;
, что соответствует формулам частотных характеристик реальных реактивных фильтров;
б) переход к операторной форме записи частотных характеристик (замена переменной 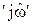 на переменную
на переменную 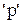 в аналитическом выражении, аппроксимирующем коэффициент передачи мощности);
в аналитическом выражении, аппроксимирующем коэффициент передачи мощности);
в) переход к выражению для входного сопротивления фильтра, используя взаимосвязь коэффициента передачи мощности, коэффициента отражения и входного сопротивления фильтра:
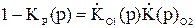 , (43)
, (43)
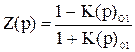 . (44)
. (44)
В выражении (44) применяется лишь один коэффициент отражения 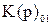 , который соответствует устойчивой электрической цепи (полюса этого коэффициента не имеют положительной действительной части);
, который соответствует устойчивой электрической цепи (полюса этого коэффициента не имеют положительной действительной части);
г) разложение аналитического выражения для входного сопротивления, полученного из (44) на сумму дробей или в ‘цепную’ дробь для получения эквивалентной схемы и значений элементов.
Полиномиальный синтез в практических разработках обычно проводится с использованием справочников по фильтрам, в которых выполнены расчеты для данного метода синтеза. В справочниках приведены аппроксимирующие функции, эквивалентные схемы и нормированные элементы фильтров нижних частот. В большинстве случаев в качестве аппроксимирующих функций применяются полиномы Баттерворта и Чебышева.
Ослабление фильтра нижних частот с аппроксимирующей функцией Баттерворта описывается выражением:
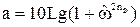 , (45)
, (45)
где 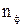 - порядок фильтра (положительное целое число, численно равное количеству реактивных элементов в эквивалентной схеме фильтра).
- порядок фильтра (положительное целое число, численно равное количеству реактивных элементов в эквивалентной схеме фильтра).
Порядок фильтра определяется выражением:
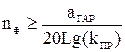 . (46)
. (46)
В таблицах 1,2 приведены значения нормированных реактивных элементов при аппроксимации Баттерворта, рассчитанные для разных порядках фильтра нижних частот (для схем, аналогичных схемам на рисунках 9, 10).
Таблица 1 – Значения нормированных элементов ФНЧ Баттерворта П - образной схемы
| 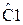
| 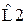
| 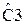
| 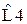
| 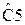
| 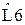
| 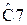
|
| 1 | 2 | ||||||
| 2 | 1,414 | 1,414 | |||||
| 3 | 1 | 2 | 1 | ||||
| 4 | 0,765 | 1,848 | 1,848 | 0,765 | |||
| 5 | 0,618 | 1,618 | 2 | 1,618 | 0,618 | ||
| 6 | 0,518 | 1,414 | 1,932 | 1,932 | 1,414 | 0,518 | |
| 7 | 0,445 | 1,242 | 1,802 | 2 | 1,802 | 1,242 | 0,445 |
Таблица 2 – значения нормированных элементов ФНЧ Баттерворта Т - образной схемы
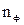
| 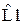
| 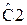
| 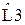
| 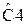
| 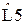
| 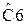
| 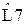
|
| 1 | 2 | ||||||
| 2 | 1,414 | 1,414 | |||||
| 3 | 1 | 2 | 1 | ||||
| 4 | 0,765 | 1,848 | 1,848 | 0,765 | |||
| 5 | 0,618 | 1,618 | 2 | 1,618 | 0,618 | ||
| 6 | 0,518 | 1,414 | 1,932 | 1,932 | 1,414 | 0,518 | |
| 7 | 0,445 | 1,242 | 1,802 | 2 | 1,802 | 1,242 | 0,445 |
При синтезе следует учитывать, что для аппроксимации Баттерворта ослабление на границе полосы пропускания обязательно равно 3 дБ.
Ослабление фильтра нижних частот с аппроксимирующей функцией Чебышева описывается выражением:
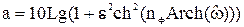 , (47)
, (47)
где 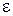 - коэффициент неравномерности, величина которого зависит от значения неравномерности ослабления в полосе пропускания
- коэффициент неравномерности, величина которого зависит от значения неравномерности ослабления в полосе пропускания
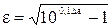 . (48)
. (48)
Для полосы задерживания существуют более простые варианты записи ослабления ФНЧ с аппроксимацией Чебышева, например:
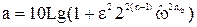 . (49)
. (49)
По формуле (49) проще определить требуемый порядок фильтра:
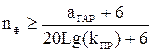 . (50)
. (50)
При аппроксимации Чебышева значения нормированных элементов для электрических схем, показанных на рисунках 9, 10, различаются при разной неравномерности в полосе пропускания, даже при неизменном порядке фильтра. В таблицах 3,4 приведены рассчитанные нормированные элементы для таких схем ФНЧ, но лишь для одного варианта - для неравномерности в полосе пропускания 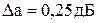 , при
, при 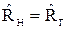 .
.
Таблица 3 – значения нормированных элементов ФНЧ Чебышева П - образной схемы
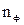
| 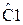
| 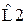
| 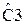
| 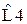
| 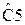
| 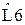
| 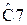
|
| 1 | 0,4668 | ||||||
| 3 | 1,3034 | 1,1463 | 1,3034 | ||||
| 5 | 1,3824 | 1,3264 | 2,2091 | 1,3264 | 1,3824 | ||
| 7 | 1,4468 | 1,3560 | 2,3476 | 1,4689 | 2,3476 | 1,3560 | 1,4468 |
Таблица 4 – значения нормированных элементов ФНЧ Чебышева Т- образной схемы
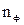
| 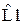
| 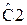
| 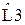
| 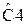
| 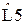
| 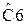
| 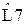
|
| 1 | 0,4668 | ||||||
| 3 | 1,3034 | 1,1463 | 1,3034 | ||||
| 5 | 1,3824 | 1,3264 | 2,2091 | 1,3264 | 1,3824 | ||
| 7 | 1,4468 | 1,3560 | 2,3476 | 1,4689 | 2,3476 | 1,3560 | 1,4468 |
Больше информации можно получить из справочников по синтезу ФНЧ [4], где приводятся не только значения нормированных элементов для разных соотношений сопротивлений внешних цепей, но также коэффициенты и полюса аппроксимирующих полиномов.
2.3.2. Последовательность синтеза ФНЧ по рабочим параметрам
При синтезе по рабочим параметрам, с использованием справочников нормированных реактивных фильтров нижних частот, используются формулы (45) – (49) данных методических указаний. Последовательность расчетов для ФНЧ следующая:
а) требования задания к синтезу ФНЧ нормируются, то есть принимается 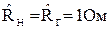 ,
, 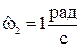 ,
, 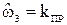 ;
;
б) определяется порядок фильтра ( 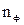 ) для одного или нескольких видов аппроксимации коэффициента передачи по формулам (46), (50) данных методических указаний. Порядок фильтра в рассматриваемых аппроксимациях равен числу идеальных реактивных элементов в схеме фильтра.
) для одного или нескольких видов аппроксимации коэффициента передачи по формулам (46), (50) данных методических указаний. Порядок фильтра в рассматриваемых аппроксимациях равен числу идеальных реактивных элементов в схеме фильтра.
Выбирается Т -, образная или П - образная эквивалентная схема, соответствующая рассчитанному порядку. Из справочников нормированных ФНЧ или из таблиц 1,2,3,4 подраздела 2.3.1 данных методических указаний выбираются значения нормированных реактивных элементов 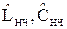 , для рассчитанного порядка фильтра;
, для рассчитанного порядка фильтра;
в) рассчитываются значения ослабления для нескольких значений нормированных частот в полосе пропускания и в полосе задерживания (без учета тепловых потерь) по формулам (45), (47). Для использования при построении графиков обычных рабочих частот, значения нормированных частот необходимо умножать на множитель 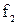 ;
;
г) элементы эквивалентной схемы ФНЧ денормируются, то есть пересчитываются к требованиям задания:
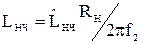 , (51)
, (51)
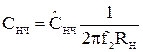 ; (52)
; (52)
д) далее проводятся расчеты по пунктам ‘д’ - ’ж’ подраздела 2.2.2 методики проектирования ФНЧ (ФВЧ ) по характеристическим параметрам.
2.3.3. Последовательность синтеза ФВЧ по рабочим параметрам
Для обеспечения возможности синтеза фильтров верхних частот с помощью справочников нормированных ФНЧ, применяют следующую методику:
а) нормируются требования задания к синтезу ФВЧ, то есть принимается 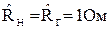 ,
, 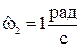 ,
, 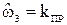 . С помощью частотного преобразования
. С помощью частотного преобразования 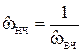 (преобразование ‘ФВЧ - ФНЧ’), требования задания к фильтру верхних частот преобразуются в требования к фильтру нижних частот. При этом
(преобразование ‘ФВЧ - ФНЧ’), требования задания к фильтру верхних частот преобразуются в требования к фильтру нижних частот. При этом 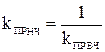 ;
;
б) проводится синтез эквивалентной схемы ФНЧ с нормированными элементами 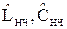 по методике пункта ‘б’ подраздела 2.3.2;
по методике пункта ‘б’ подраздела 2.3.2;
в) с помощью обратного частотного преобразования ‘ФНЧ - ФВЧ’ схема фильтра нижних частот преобразуется в схему фильтра верхних частот с нормированными элементами 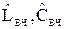 , причем:
, причем:
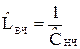 , (53)
, (53)
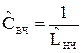 ; (54)
; (54)
г) рассчитываются значения ослабления для нескольких значений частот в полосе пропускания и в полосе задерживания без учета тепловых потерь для нормированных частот. Для ФВЧ Баттерворта – по формуле:
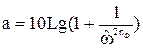 . (55)
. (55)
Для ФВЧ Чебышева – по формуле:
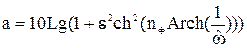 , (56)
, (56)
Для перехода от нормированных частот к обычным рабочим, как и ранее для ФНЧ, значения нормированных частот необходимо умножить на множитель 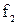 ;
;
д) элементы эквивалентной схемы ФВЧ денормируются, то есть пересчитываются к требованиям задания:
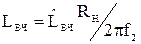 , (57)
, (57)
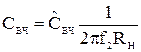 ; (58)
; (58)
д) далее проводятся расчеты по пунктам ‘д’ - ’ж’ подраздела 2.2.2 методики проектирования ФНЧ (ФВЧ ) по характеристическим параметрам.
2.3.4. Последовательность синтеза ПФ (РФ) по рабочим параметрам
При синтезе схем ПФ или РФ по рабочим параметрам также, как и при синтезе подобных фильтров по характеристическим параметрам, вначале рекомендуется рассчитать эквивалентные схемы фильтров-прототипов: для ПФ - фильтра нижних частот, для РФ - фильтра верхних частот. В связи с этим:
а) на первом этапе синтеза, как и в подразделе 2.2.3, необходимо применить частотное преобразование ‘ПФ – ФНЧ’ или ‘РФ – ФВЧ’, то есть пересчитать заданные в задании требования по ослаблению, в ослабление фильтра-прототипа, используя соотношения между частотами 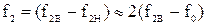 ,
, 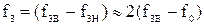 ;
;
б) далее, в зависимости от задания, разрабатывается схема нужного фильтра-прототипа (либо схема ФНЧ по методике подраздела 2.3.2 (для ПФ), либо – схема ФВЧ по методике подраздела 2.3.3 (для РФ)). Для фильтра-прототипа рассчитываются и строятся графики ослабления и коэффициента передачи по напряжению;
в) для заключительных этапов синтеза ПФ или РФ применяется методика подраздела 2.2.3, по которой эквивалентные схемы фильтров-прототипов преобразуются в соответствующие эквивалентные схемы полосового или режекторного фильтра. Затем по этой же методике разрабатываются схемы электрические принципиальные ПФ или РФ и пересчитываются графики ослабления и коэффициента передачи по напряжению фильтров-прототипов в графики ПФ или РФ (формулы (41), (42)).
2.4. Пример синтеза эквивалентной схемы электрического фильтра
2.4.1. Исходные данные к проектированию
- тип фильтра – ФВЧ;
- 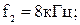
- 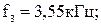
- 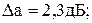
- 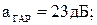
- 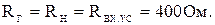
2.4.2. Синтез эквивалентной схемы ФВЧ
- выбран метод синтеза по характеристическим параметрам, при котором расчетная неравномерность в полосе пропускания 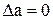 , то есть требования по этому параметру выполняются;
, то есть требования по этому параметру выполняются;
- требования к ослаблению ФВЧ соответствуют рисунку 5а;
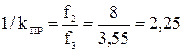 ;
;
значения элементов эквивалентной схемы звена ФНЧ (рисунок 5б) равны:
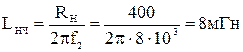 ,
,
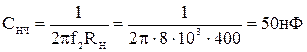 ;
;
- ослабление звена на граничной частоте полосы задерживания равно:
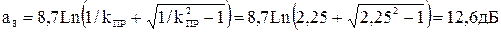 ;
;
- количество каскадно соединенных звеньев ФНЧ:
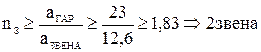 ;
;
- ослабление двухзвенного фильтра верхних частот на граничной частоте полосы задерживания определяется:
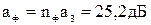 ;
;
- рассчитывается ослабление ФВЧ для нескольких значений частоты в полосе задерживания без учета тепловых потерь, в соответствии с формулой (32):
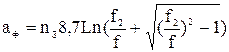 ;
;
рассчитывается ослабление ФНЧ в полосе пропускания и в полосе задерживания для нескольких значений частоты с учетом тепловых потерь, по формулам (34), (35):
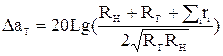 ,
, 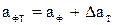 ;
;
- определяется коэффициент передачи ФВЧ по напряжению для нескольких значений частоты в полосе пропускания и в полосе задерживания, в соответствии с формулой (36):
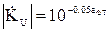 ;
;
затем строятся графики для ФВЧ, выбираются или рассчитываются радиоэлементы схемы электрической принципиальной.








