2. Основные принципы и методы проектирования электрических фильтров
2.1. Основные принципы проектирования фильтров
2.1.1. Основные требования к проектированию
Электрические фильтры – это линейные или ‘квазилинейные’ электрические цепи, имеющие частотно-зависимые комплексные коэффициенты передачи полной мощности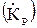 
. При этом, частотно-зависимым является также хотя бы один из двух коэффициентов передачи: по напряжению 
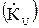или по току 
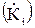. Вместо безразмерных коэффициентов передачи при анализе и синтезе фильтров широко применяется ослабление ( 
), измеряемое в децибеллах:
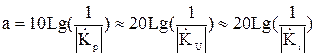, (1)
где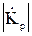 
, 
, 
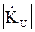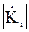- модули коэффициентов передачи (в формуле (1) - применяется десятичный логарифм).
Частотный диапазон, в котором ослабление ( 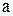) приближается к нулю, а коэффициент передачи полной мощности ( 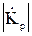) приближается к единице, называется полосой пропускания (ПП). И наоборот, в частотном диапазоне, где, коэффициент передачи мощности близок к нулю, а ослабление составляет несколько десятков децибел – находится полоса задерживания (ПЗ). Полосу задерживания в специальной литературе по электрическим фильтрам также называют полосой ослабления или полосой затухания. Между ПП и ПЗ находится ‘переходная’ полоса частот. По расположению полосы пропускания в частотном диапазоне, электрические фильтры относят к следующим типам:
ФНЧ – фильтр нижних частот, полоса пропускания находится на ‘нижних’ частотах;
ФВЧ – фильтр верхних частот, полоса пропускания находится на ‘верхних’ частотах;
ПФ – полосовой фильтр, полоса пропускания находится в относительно узком частотном диапазоне;
РФ – режекторный фильтр, полоса задерживания находится в сравнительно узком частотном диапазоне.
Реальный электрический фильтр может быть выполнен на различных радиокомпонентах: катушках индуктивности и конденсаторах, избирательных усилительных устройствах, избирательных пьезоэлектрических и электромеханических устройствах, волноводах и многих других. Существуют справочники по расчету фильтров на вполне определенных радиокомпонентах. Однако более универсальным является следующий принцип: вначале разрабатывается эквивалентная схема на идеальных LC - элементах, а затем идеальные элементы пересчитываются в любые реальные радиокомпоненты. При таком пересчете и разрабатывается схема электрическая принципиальная, перечень элементов, выбираются стандартные или проектируются самостоятельно необходимые радиокомпоненты. Наиболее простым вариантом подобного расчета является разработка принципиальной схемы реактивного фильтра с конденсаторами и катушками индуктивности, так как принципиальная схема в этом случае подобна эквивалентной.
Но и при таком общем универсальном расчете существует несколько различающиеся между собой методов синтеза эквивалентной схемы LC – фильтра, а именно:
- синтез в согласованном режиме из одинаковых Г-, Т-, П- образных звеньев[3]. Этот метод также называют синтезом по характеристическим параметрам или синтезом фильтров типа “k”. Достоинства: простые расчетные формулы; рассчитанное ослабление (неравномерность ослабления) в полосе пропускания (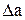 
) принимается равным нулю. Недостаток: в этом методе синтеза используются различные приближения, на самом же деле согласование во всей полосе пропускания получить невозможно. Поэтому у фильтров, рассчитанных этим методом, ослабление в полосе пропускания может быть более трех децибел; 
- полиномиальный синтез [4,5]. В этом случае требуемый коэффициент передачи мощности аппроксимируется полиномом, то есть синтезируется вся схема, а не отдельные звенья. Этот метод также называют синтезом по рабочим параметрам или синтезом ‘по справочникам нормированных ФНЧ’. При использовании справочников, рассчитывается порядок фильтра, выбирается эквивалентная схема ФНЧ, удовлетворяющая требованиям задания. Достоинства: в расчетах учитываются возможные несогласования и отклонения параметров радиоэлементов, ФНЧ легко преобразуются в фильтры других типов. Недостаток: необходимо пользоваться справочниками или специальными программами;
- синтез по импульсным или переходным характеристикам. Основан на взаимосвязи временных и частотных характеристик электрических цепей через различные интегральные преобразования (Фурье, Лапласа, Карсона и другие). Например, импульсная характеристика (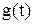 
) выражается через передаточную характеристику ( 
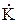) с помощью прямого преобразования Фурье:
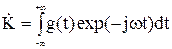. (2)
Этот метод нашел применение при синтезе различных трансверсальных фильтров (фильтров с задержками), например, цифровых, акустоэлектронных, для которых разработать электрические схемы проще по импульсным характеристикам, чем по частотным характеристикам. В данной курсовой работе при разработке схем фильтров, рекомендуется применять метод синтеза по характеристическим или рабочим параметрам.
Итак, в работе касающейся синтеза электрического фильтра, необходимо одним из методов разработать схему электрическую эквивалентную на идеальных реактивных элементах, а затем схему электрическую принципиальную на любых реальных радиоэлементах.
В задании к курсовому проектированию в части, касающейся синтеза электрического фильтра (приложение ‘Б’), могут быть приведены следующие данные:
- тип синтезируемого фильтра (ФНЧ, ФВЧ, ПФ, РФ);
- 
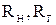- активные сопротивления внешних цепей, с которыми полностью или частично должен быть согласован фильтр в полосе пропускания;
- 
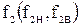- граничная частота полосы пропускания фильтра;
- 
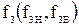- граничная частота полосы задерживания фильтра;
- 
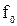- средняя частота фильтра (для ПФ и РФ);
- 
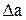– ослабление фильтра в полосе пропускания, (не более);
- 
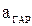- ослабление фильтра в полосе задерживания, (не менее);
- 
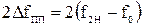- полоса пропускания ПФ или РФ;
- 
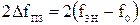- полоса задерживания ПФ или РФ;
- 
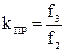- коэффициент прямоугольности ФНЧ, ФВЧ;
- 
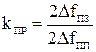- коэффициент прямоугольности ПФ, РФ.
При необходимости студенты могут самостоятельно выбрать дополнительные данные или требования к проектированию.
2.1.2. Нормирование и частотные преобразования
При синтезе эквивалентных и принципиальных схем фильтров целесообразно применять нормирование и частотные преобразования. Это позволяет уменьшить количество разнотипных расчетов и проводить синтез, взяв за основу фильтр нижних частот. Нормирование заключается в следующем. Вместо проектирования на заданные рабочие частоты и сопротивления нагрузки, проектируются фильтры на нормированное сопротивление нагрузки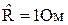 
и нормированные частоты 
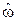. Нормирование частот осуществляется как правило относительно частоты 
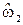.. При таком нормировании частота 
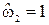, а частота 
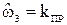. При нормировании вначале разрабатывается эквивалентная схема с нормированными элементами 
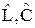, а затем эти элементы пересчитываются к заданным требованиям с помощью денормирующих множителей:
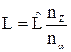, (3)
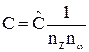, (4)
где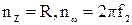 
.
Возможность применения нормирования при синтезе электрических цепей следует из того, что вид требуемых передаточных характеристик электрической цепи при этой операции не изменяется, они лишь переносятся на другие (нормированные) частоты.
Например, для схемы – делителя напряжения, показанной на рисунке 2, коэффициент передачи по напряжению аналогичен как при заданных радиоэлементах и рабочей частоте, так и при нормированных величинах – при применении нормирующих множителей.
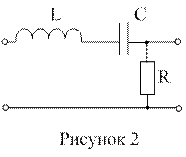
Без нормирования:
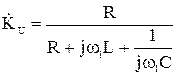, (5)
с нормированием:
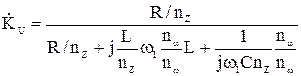. (6)
В выражении (6), в общем случае, нормирующие множители, могут быть произвольными действительными числами.
Дополнительное применение частотных преобразований позволяет существенно упростить синтез ФВЧ, ПФ, РФ. Так, рекомендуемая последовательность синтеза ФВЧ, при применении частотных преобразований, следующая:
- графические требования к ФВЧ нормируются (вводится ось нормированных частот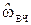 
);
- производится частотное преобразование требований к ослаблению, за счет преобразования частот:
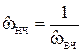; (7)
- проектируется ФНЧ с нормированными элементами;
- ФНЧ преобразуется в ФВЧ с нормированными элементами;
- элементы денормируются, в соответствии с формулами (3), (4).
Рекомендуемая последовательность синтеза полосового фильтра, при использовании частотных преобразований, следующая:
- графические требования к ПФ заменяются на требования к ФНЧ из условия равенства их полос пропускания и задерживания;
- синтезируется схема фильтра нижних частот;
- применяется обратное частотное преобразование для получения схемы полосового фильтра, включением в ‘ветви’ ФНЧ дополнительных реактивных элементов для образования резонансных контуров;
Рекомендуемая последовательность синтеза режекторного фильтра, при использовании частотных преобразований:
- графические требования к РФ заменяются на требования к ФВЧ из условия равенства их полос пропускания и задерживания;
- синтезируется схема фильтра верхних частот, непосредственно или с использованием прототипа – фильтра нижних частот;
- схема ФВЧ преобразуется в схему режекторного фильтра, включением в ‘ветви’ ФВЧ дополнительных реактивных элементов.
2.2 Методика синтеза фильтров по характеристическим параметрам
2.2.1. Основные положения синтеза по характеристическим параметрам
Обоснование основных расчетных соотношений этого метода синтеза, следующее.
Рассматривается линейный четырехполюсник, для его описания используется система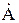 
- параметров:
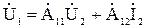, (8)
,
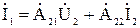где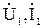 
- напряжение и ток на входе четырехполюсника, 
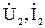- напряжение и ток на выходе четырехполюсника.
Определяются коэффициенты передачи для произвольного (согласованного или несогласованного) режима:
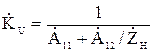, (9)
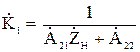, (10)
где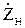 
- сопротивление нагрузки (в общем случае комплексное).
Для произвольного режима вводится постоянная передачи (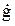 
), ослабление ( 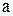), фаза ( 
):
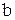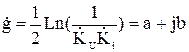(11)
Ослабление в неперах определяется выражением:
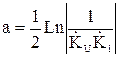, (12)
а в децибелах – выражением:
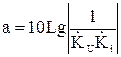. (13)
В несогласованном режиме входные, выходные и передаточные характеристики четырехполюсника называются рабочими параметрами, а в согласованном режиме – характеристическими. Значения согласующих входного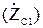 
и выходного 
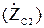сопротивлений на заданной рабочей частоте определяются из уравнений четырехполюсника (8):
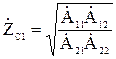, (14)
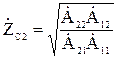. (15)
В согласованном режиме, с учетом выражений (14), (15) характеристическая постоянная передачи определяется:
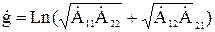. (16)
С учетом соотношений для гиперболических функций
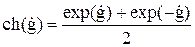, (17)
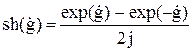, (18)
определяется взаимосвязь между характеристическими параметрами согласованного режима и элементами электрической схемы ( 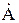- параметрами). Выражения имеют вид:
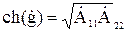, (19)
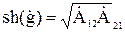. (20)
Выражения (19), (20) характеризуют согласованный режим произвольного линейного четырехполюсника. На рисунке 3 показана схема произвольного Г- образного звена, - параметры которой, в соответствии с выражениями (8), определяются:
, 
, 
, 
.
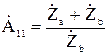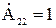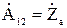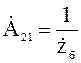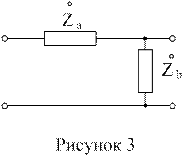
При согласованном включении Г- образного звена, выражения (19), (20) преобразуются к виду:
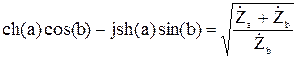, (21)
. (22)
Если в продольной и поперечной ветвях Г- образной схемы находятся разнотипные реактивные элементы, то схема является электрическим фильтром.
Анализ формул (21), (22) для этого случая позволяет получить методику синтеза фильтров по характеристическим параметрам. Основные положения этой методики:
- фильтр проектируется из одинаковых, включенных каскадно, согласованных в полосе пропускания друг с другом и с внешними нагрузками, звеньев (например, звеньев Г-типа);
- ослабление в полосе пропускания (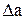 
) принимается равным нулю, так как во всей полосе пропускания фильтр считается согласованным;
- требуемые величины внешних активных сопротивлений (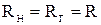 
) для согласованного режима определяются через сопротивления ‘ветвей’ Г- образного звена по приближенной формуле:
; (23)
- граничная частота полосы пропускания (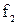 
) определяется из условия:
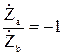; (24)
- ослабление звена (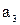 
) на граничной частоте полосы задерживания ( 
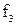) определяется (в децибелах) по формуле:
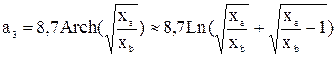; (25)
- количество одинаковых Г - звеньев, включаемых каскадно, определяется выражением:
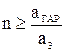. (26)