Таким образом, действующее значение несинусоидального тока является средней квадратичной величиной постоянной составляющей и действующих значений токов гармоник.
Аналогично действующее значение несинусоидального напряжения определяется выражением
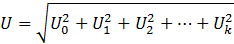
Действующее значение несинусоидального напряжения является средней квадратичной величиной постоянной составляющей и действующих значений напряжений гармоник
Под активной мощностью Р несинусоидального тока понимают среднее значение мгновенной мощности за период.
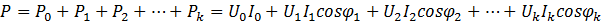
где Р0 — мощность постоянной составляющей несинусоидального тока;
Р1 Р2, , Рk — активные мощности гармоник несинусоидального тока.
Таким образом, потребляемая, т. е. активная, мощность в цепи несинусоидального тока определяется суммой постоянной мощности и активных мощностей гармоник.
Реактивная мощность в цепи несинусоидального тока, по аналогии, определяется выражением
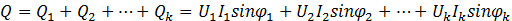
Реактивная мощность в цепи несинусоидального тока определяется суммой реактивных мощностей гармоник.
Постоянная составляющая реактивной мощности отсутствует, так как для постоянного тока колебание мощности (энергии) немыслимо.
Полная, или кажущаяся, мощность в цепях несинусоидального тока равна
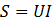
Следует иметь в виду, что несинусоидальный ток или напряжение не могут быть выражены при помощи векторов. Кривые несинусоидального тока и напряжения в общем случае даже не подобны. Так что невозможно применить понятие об угле сдвига фаз, принятое для синусоидальных токов.
Поэтому при изучении некоторых свойств цепей несинусоидального тока несинусоидальные токи и напряжения заменяют эквивалентными синусоидальными. Замена производится таким образом, что действующее значение синусоидального тока принимается равным действующему значению заменяемого несинусоидального тока, а действующее значение синусоидального напряжения принимается равным действующему значению несинусоидального напряжения.
Тогда угол сдвига фаз φ между эквивалентными синусоидами напряжения и тока выбирается таким, чтобы активная мощность эквивалентного синусоидального тока была равна активной мощности несинусоидального тока, т.е.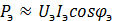 
Откуда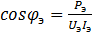 
При этом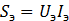 
.Однако для цепи несинусоидального тока в общем случае
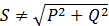
Пример 6
Определить действующие значения тока, напряжения, активную мощность цепи и коэффициент мощности. Написать уравнение мгновенного значения тока цепи, если R = 50 Ом, ХL =10 Ом, ХС = 90 Ом соединены последовательно (рис. 12), а приложенное напряжение задано уравнением
u = 268 sin ω t+70,5 sin3 ω t + 42 sin 5ω t, В
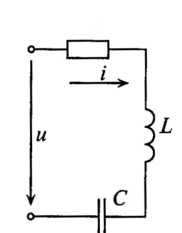
Рисунок 12 – Расчетная схема
Решение
1. Определяем полное сопротивление цепи для первой гармоники.
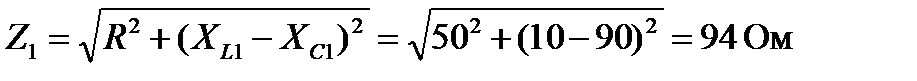
2. Определяем максимальное значение тока первой гармоники.
I m1 = Um1 / Z1=268 / 94=2,84 А
3. Действующее значение тока первой гармоники.
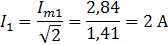
4. Сдвиг фаз между током и напряжением первой гармоники.
tg φ1 = (XL1 - XС1)/R = (10 - 90)/50 = - 1.6; φ1 = - 580
5. Определяем полное сопротивление цепи для третьей гармоники.
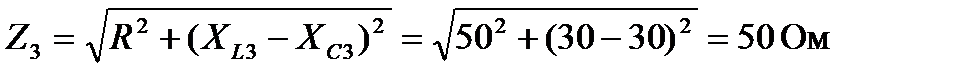
где XL3=3 ∙XL1= 3∙10 = 30 Ом; XС3 = XС1/ 3 = 90/3 = 30 Ом
6. Определяем максимальное значение тока третьей гармоники.
I m3 = Um3 / Z3 = 70, 5/ 50 = 1,41 A .
7. Действующее значение тока третьей гармоники.
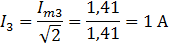
8. Сдвиг фаз между током и напряжением третьей гармоники.
tg φ3 = (XL3 - XС3)/R=(30 – 30) / 50 = 0; φ3 = 00
9. Определяем полное сопротивление цепи для пятой гармоники.
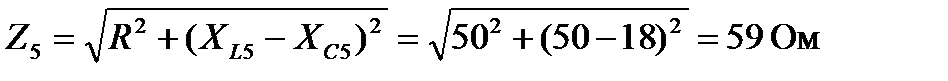
где XL5=5 ∙XL1= 5∙10 = 50 Ом; XС5 = XС1/ 5 = 90/5 = 18 Ом
10.Определяем максимальное значение тока пятой гармоники.
I m5 = Um5 / Z5 = 42 / 59 = 0,73 A.
11.Действующее значение тока пятой гармоники.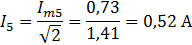 
12.Сдвиг фаз между током и напряжением пятой гармоники.
tg φ5 = (XL5 – XС5)/R=(50 – 18) / 50 = 0,64; φ5 = 330
13.Действующее значение несинусоидального тока цепи.
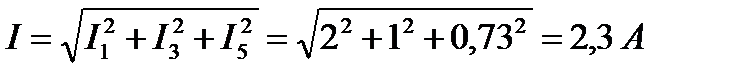
14. Действующее значение несинусоидального напряжения цепи.
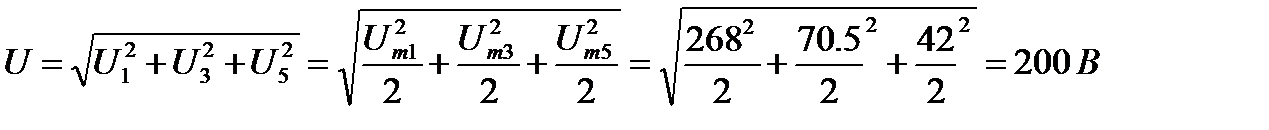
15. Активная мощность цепи.
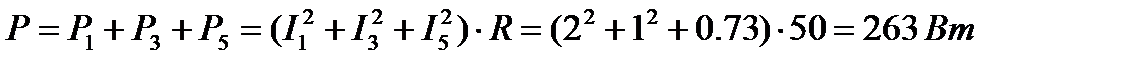
16. Реактивная мощность цепи
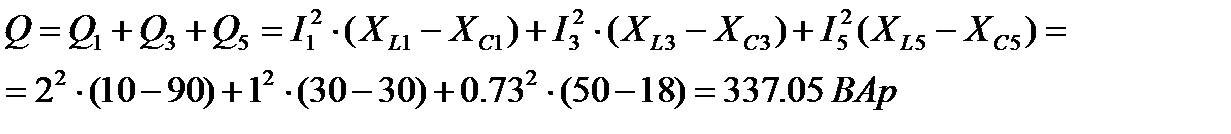
17. Полная мощность цепи
S = U∙I = 200 ∙ 2.3 = 460 В∙А.
18. Коэффициент мощности цепи.
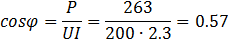
1. Уравнение мгновенного значения тока цепи.
I = Im 1 ∙ sin ( ω t – φ 1 ) + Im 3 ∙ sin (3 ω t – φ 3 ) + Im 5 ∙ sin (5 ω t – φ 5 ) =
= 2.84∙ sin ( ω t + 580) + 1.41∙ sin 3 ω t + 0.73∙ sin (5 ω t –330) А.
Методические указания к решению задачи 5
Задача 5 относится к теме «Нелинейные электрические цепи переменного тока». Наиболее распространенным нелинейным элементом переменного тока в электрических машинах, трансформаторах и других аппаратах является катушка со стальным сердечником. Задача 5 предусматривает расчет катушки со стальным сердечником.
КРАТКИЕ СВЕДЕНИЯ