Пример 4 Символический метод расчета электрических цепей переменного тока
Пользуясь символическим методом, определить токи, напряжения и мощности во всех участках схемы, изображенной на рисунке 6. Необходимые данные приведены в таблице 5.
Вычертить схему цепи, учитывая характер нагрузки во всех ее участках (согласно исходным данным)
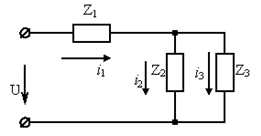
Рисунок 6 – Электрическая схема
Составить баланс активных и реактивных мощностей для проверки правильности решения задачи.
В масштабе построить векторную диаграмму токов и напряжений цепи на комплексной системе координат.
Таблица 5 - Исходные данные к примеру 4
| U, В | Z1, Ом | Z2, Ом | Z3,0м | |||
| R1, Ом | X1, Ом | R2, Ом | Х2, Ом | RЗ, Ом | ХЗ, Ом | |
| 180 | 15 | 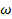 L1 = 12 L1 = 12
| 5 | 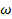 L2 = 12 L2 = 12
| 9 | 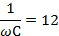
|
Решение:
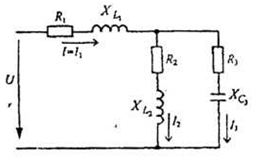 1 В соответствии с данными составим схему (рис. 7)
1 В соответствии с данными составим схему (рис. 7)
Рисунок 7 - Электрическая схема
2 Запишем комплексы полных сопротивлений всех участков цепи:
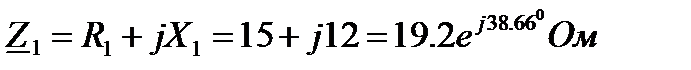
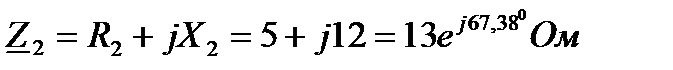
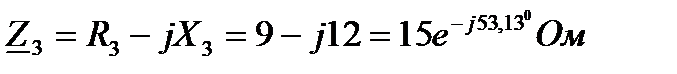
3 Комплексное полное сопротивление разветвления:
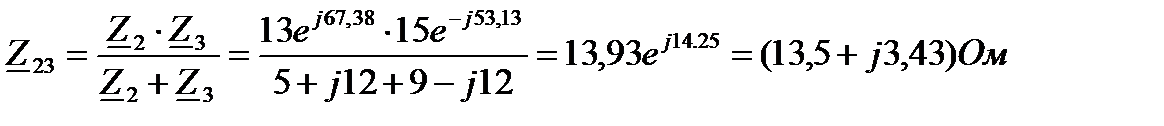
4 Комплекс полного сопротивления всей цепи:
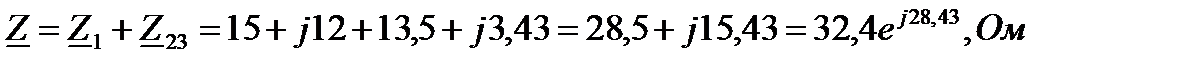
5 Совместим вектор напряжения на входных зажимах цепи с осью действительных величин 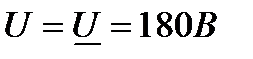
6 Комплексный ток в неразветвленной части цепи, по закону Ома будет равен
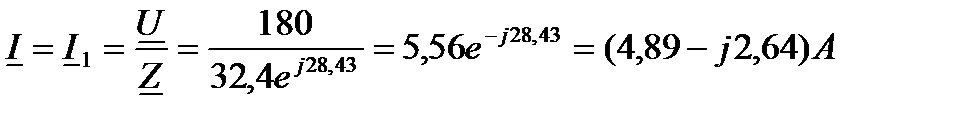
7 Комплексное напряжение на неразветвленном участке цепи:
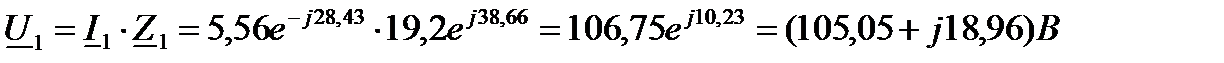
8 Комплексное напряжение на разветвленном участке цепи:
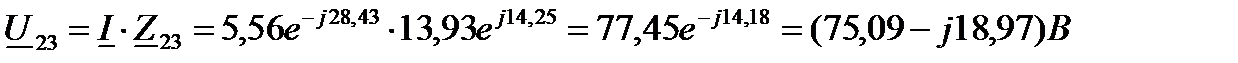
9 Комплексные токи в параллельных ветвях:
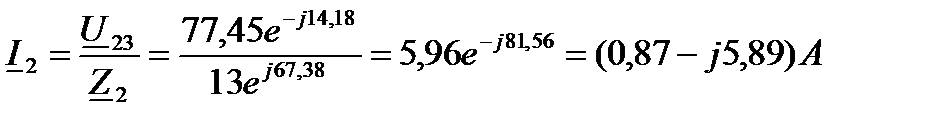
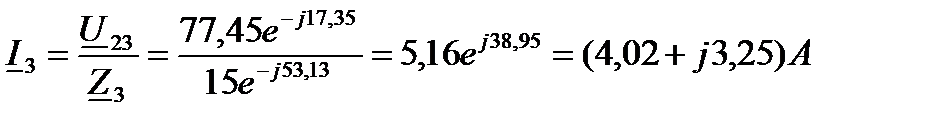
10 Определим полные комплексные мощности отдельных участков цепи:
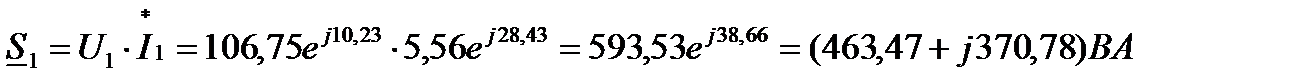
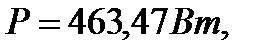
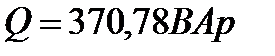
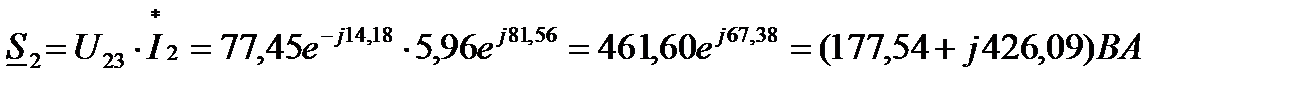
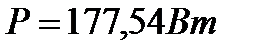
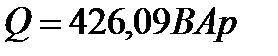
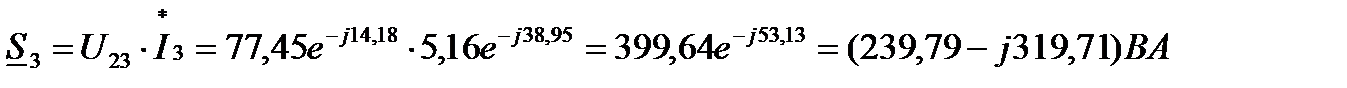
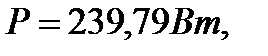
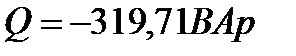
11 Комплекс полной мощности всей цепи:
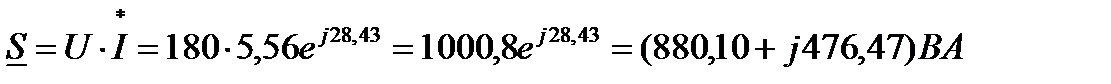
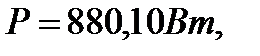
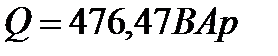
12 Проверка.
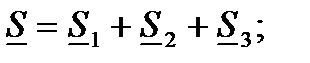
880,10 + j476,47=463,47 + j370,78+177,54+j426,09+239,79 – j319,71
880,10 + j476,47 ~ 880,80 + j477,16
т. е. задача решена, верно.
12.В масштабе mI = 2 А/см, mU = 15 В/см на комплексной плоскости строим векторную диаграмму токов и напряжений цепи. Определяем длины векторов токов и напряжений, а из расчета выписываем аргументы комплексных токов и напряжений.
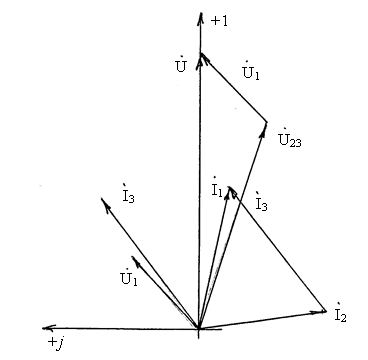
Рисунок 8 - Векторная диаграмма
Методические указания к решению задачи 3
Эти задачи относится к трехфазным электрическим цепям переменного синусоидального тока
КРАТКИЕ СВЕДЕНИЯ
В трехфазных цепях потребители соединяют по схеме «звезда» или «треугольник».
При соединении приемников энергии «звездой» линейные напряжения обозначаются UAB, UBC. UCA, а в общем виде – UЛ; фазные напряжения обозначаются UA, UB. UC, а в общем виде – Uф
Токи обозначаются - IA, IB. IC, причем ток линейный равен току фазному, поэтому в общем виде Iл = Iф
При наличии нулевого провода при любой нагрузке, а при равномерной нагрузке и без нулевого провода 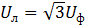 (линейное напряжение больше фазного в
(линейное напряжение больше фазного в 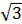 раз). При равномерной нагрузке фаз активная мощность всей цепи
раз). При равномерной нагрузке фаз активная мощность всей цепи 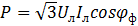 или
или 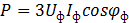 При неравномерной нагрузке мощность всей цепи Р = Рф1+Рф2+Рф3, где
При неравномерной нагрузке мощность всей цепи Р = Рф1+Рф2+Рф3, где 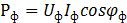 .
.
При соединении потребителей треугольником фазное напряжение равно линейному: Uф = Uл, обозначаются напряжения UAB, UBC. UCA
Фазные токи обозначаются IA, IB. IC, в общем виде - Iф. Линейные токи обозначаются IAB, IBC. ICA, в общем виде - Iл. При равномерной нагрузке фаз 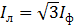 .
.
При неравномерной нагрузке фаз линейные токи определяются на основании первого закона Кирхгофа из векторной диаграммы, как геометрическая разность фазных токов.
При соединении приемников энергии «звездой» сеть может быть четырехпроводной - при наличии нулевого провода, или трехпроводной - без нулевого провода
При соединении приемников энергии “треугольником” сеть может быть только трехпроводной.
Четырехпроводная трехфазная цепь позволяет присоединить:
а) трехфазные приемники к трем линейным проводам;
б) однофазные приемники между каждым линейным проводом и нейтральным.
Пример 5
На рисунке 9 показана трехфазная сеть, питающая две нагрузки, одна из которых соединена звездой, другая - треугольником. Система линейных напряжений симметрична UАВ= UВС= UСА=UЛ = 380 В.
Приемник энергии, соединенный звездой, имеет мощности фаз РА = 2200 Вт; РН = 4840 Вт; РС = 7700 Вт; коэффициент мощности cos φ γ = 1(φ = 00).
Приемник энергии, соединенный треугольником, - симметричный, мощности фаз РАВ = РВС = РСА = 4260 Вт; cos φ ∆ = 0.866 (φ ∆ = 300); характер нагрузки – активно – индуктивный.
Определить фазные и линейные токи нагрузок, токи в проводах линии, питающей обе нагрузки, и ток в нейтральном проводе.
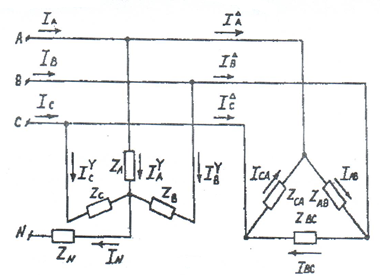
Рисунок 9 -Трехфазная цепь
Решение
Фазные напряжения нагрузки, соединенной звездой, благодаря нейтральному проводу равны:
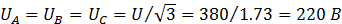
Фазные (линейные) токи нагрузки, соединенные звездой,
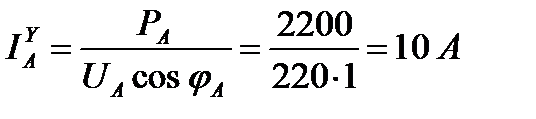
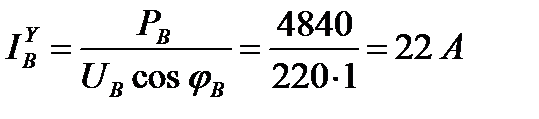
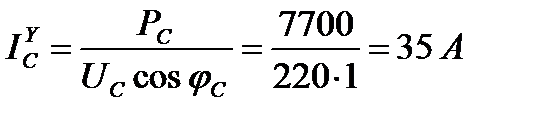
Согласно первому закону Кирхгофа для нейтральной точки N имеем:
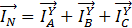
Следовательно, построив симметричную трехлучевую звезду фазных напряжений и отложив вдоль этих напряжений соответствующие фазные точки (так как 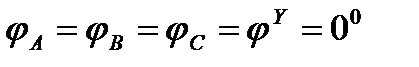 , поскольку
, поскольку 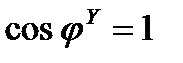 ), можно, геометрически сложив эти токи, определить вектор тока
), можно, геометрически сложив эти токи, определить вектор тока 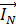 в нейтральном проводе (см. рисунок 10).
в нейтральном проводе (см. рисунок 10).
Зададимся масштабами mu = 55 В/см и mi = 10 А/см
Производим указанное построение и графическим путем определяем
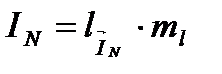 = 2 · 10 = 20 A
= 2 · 10 = 20 A
Согласно условию задачи трехфазный приемник, соединенный треугольником, - активно-индуктивный и, следовательно, фазные токи 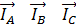 отстают по фазе относительно вызывающих их напряжений
отстают по фазе относительно вызывающих их напряжений 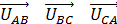 соответственно на угол
соответственно на угол 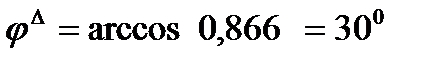 . По величине эти фазные токи равны
. По величине эти фазные токи равны
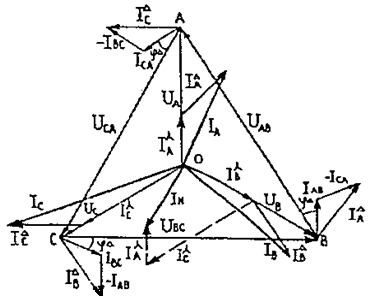
Рисунок 10 - Векторная диаграмма
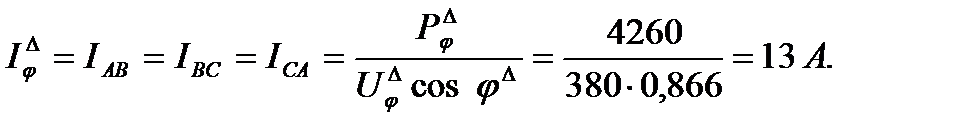
причем 
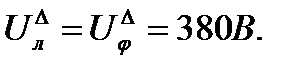
Соблюдая условия сдвига, длины векторов и выбранный масштаб токов m1, производим построение векторов фазных токов 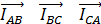
На основании первого закона Кирхгофа, примененного в узловых точках-вершинах треугольника, имеем:
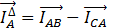
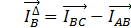
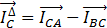
На основании этих равенств строим векторы линейных токов нагрузки, соединенной треугольником.
При симметричной нагрузке в фазах треугольника линейный ток больше фазного в 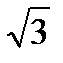 раз и отстает на 300 по фазе о первого из двух составляющих фазных токов
раз и отстает на 300 по фазе о первого из двух составляющих фазных токов
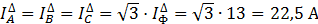
Проверка с помощью векторной диаграммы, например,
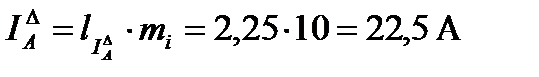 и т.д.
и т.д.
Суммарные токи в проводах линии, питающей обе нагрузки, определяют графическим путем на основании первого закона Кирхгофа
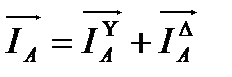
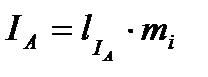
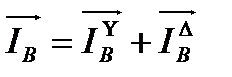
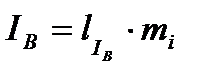
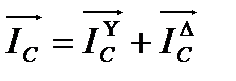
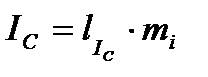
где l –длина вектора тока, получена из векторной диаграммы непосредственным измерением. Отсюда видно, что ток в нейтрально проводе непосредственно не фигурирует в выражениях суммарных линейных токов
Методические указания к решению задачи 4
Эти задачи относятся к теме «Электрические цепи с несинусоидальными периодическими токами и напряжениями». Для их решения необходимо свойства периодических кривых.
КРАТКИЕ СВЕДЕНИЯ








