Ток, напряжение и сопротивление в комплексном виде
Если ток и напряжение изменяются по синусоидальному закону i = Imsin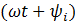 
, и = Umsin 
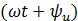,, то их можно изобразить векторами и, следовательно, записать комплексными числами:
,
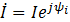
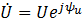где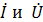 
— комплексы тока и напряжения. Точка над комплексами указывает, что ток и напряжение изменяются по синусоидальному закону с определенной частотой 
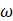; I и U — модули комплексов тока и напряжения, они же действующие значения тока 
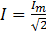и напряжения 
; 
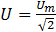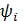и 
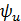— аргументы комплексов тока и напряжения, они же начальные фазы тока 
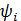, и напряжения .
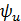Комплекс полного сопротивления цепи Z определяется отношением комплекса напряжения к комплексу тока, т. е.
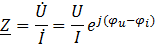
Комплексные величины, не зависящие от времени, обозначаются прописными буквами с черточкой внизу.
Модулем комплекса полного сопротивления является кажущееся сопротивление цепи Z = 
, а аргументом — угол сдвига фаз между напряжением и током φ.
Алгебраическая форма записи комплекса полного сопротивления Z
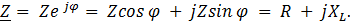
Вещественная часть комплекса полного сопротивления есть активное сопротивление R , а коэффициент при мнимой единице j — реактивное сопротивление X. Знак перед поворотным множителем (мнимой единицей) указывает на характер цепи. Знак «плюс» соответствует цепи индуктивного характера, а знак «минус» — цепи емкостного характера.
Любую цепь переменного тока можно рассчитывать по законам постоянного тока, если все величины представить в комплексной форме. В этом и заключается достоинство символического метода расчета.
Мощность в комплексном виде
Комплекс полной мощности цепи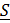 
определяется произведением комплекса напряжения 
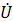и сопряженного комплекса тока 
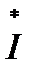(над сопряженным комплексом синусоидальной величины ставят «звёздочку»)
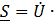
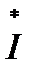
Таким образом, модулем комплекса полной мощности S является кажущаяся мощность цепи S = UI , а аргументом — угол сдвига фаз между током и напряжением.
Если комплекс полной мощности S перевести из показательной формы в алгебраическую, то получится
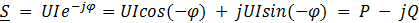
To есть вещественная часть комплекса полной мощности — активная мощность Р, а коэффициент при мнимой единице — реактивная мощность Q .
Знак перед поворотным множителем j указывает на характер цепи. В рассматриваемой цепи реактивная мощность емкостного характера (- jQ).
Комплексы величин токов, напряжений, сопротивлений, мощностей и других параметров цепи синусоидального тока необходимо выражать в двух видах записи комплексного числа: показательной и алгебраической. В этом случае сразу определяются действующие значения тока, напряжения, кажущееся сопротивление, его активные и реактивные части ( R и X), угол сдвига фаз φ между током и напряжением, характер цепи, кажущаяся S , активная Р и реактивная Q мощности. Кроме того, в неразветвленной цепи напряжения на участках складываются, суммируются токи в разветвленных цепях, а сложение комплексов можно производить только в алгебраической форме записи. В алгебраической форме записи кажущейся мощности S сразу определяются активная мощность Р и реактивная мощность Q. В показательной форме записи сопротивлений производится их умножение и деление, необходимое при расчете цепей синусоидального тока при смешанном соединении потребителей, и т.д. Необходимость выражения комплексов в двух видах следует из примера 4.