Комплексным числам соответствуют векторы , изображенные на комплексной плоскости (рис. 5 а и б) в масштабе.
Модуль комплексного числа соответствует длине вектора, изображающего это комплексное число.
Из построения (рис. 5 а) видно, что модули комплексных чисел определяются выражением
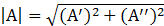
Следовательно,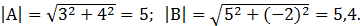 
Углы αиβ, образованные векторами 
с положительным направлением вещественной оси, называются аргументами комплексного числа.
Аргументы комплексного числа (рис.5а) определяются выражением
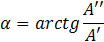
То есть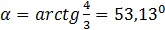 
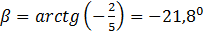
Как видно, аргумент комплексного числа В отрицательный, так как вектор В повернут на угол β по часовой стрелке, а не против.
Существует три формы записи комплексного числа:
a. алгебраическая: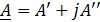 
b. тригонометрическая: A =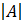 
· cosα + j 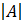· sinα
так как А'= 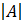· cosα, a А" = 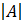· sinα.
c. показательная: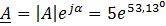 
; 
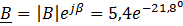
где е — основание натурального логарифма, однако в данном случае имеет чисто символическое значение.
Для перевода из показательной формы записи комплексного числа в алгебраическую пользуются тригонометрической формой записи комплексного числа.
Для перевода из алгебраической формы записи комплексного числа в показательную определяют модуль и аргумент комплексного числа.
Для перевода комплексного числа из одной формы в другую можно использовать микрокалькулятор.
Комплексные числа можно складывать, вычитать, умножать и делить.
Сложение и вычитание комплексных чисел производится только в алгебраической форме
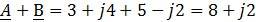
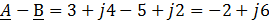
На рис. 5б видно, что сложение и вычитание комплексных чисел соответствует сложению и вычитанию векторов, изображающих эти числа.
Умножение и деление комплексных чисел можно производить в алгебраической форме:
,
.
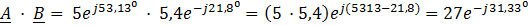Таким образом, сложение и вычитание комплексных чисел можно производить только в алгебраической форме, а умножение и деление удобней и проще производить в показательной форме.
Для цепей переменного тока, так же как и для цепей постоянного тока, справедливы закон Ома, законы Кирхгофа, формулы мощности, свойства последовательного и параллельного соединений. Поэтому все основанные на их использовании методы расчета цепей применимы и для цепей переменного тока.
Однако из-за того, что в переменном токе действует три вида совершенно различных по характеру сопротивлений (активное R, индуктивное ХL и емкостное ХC) форма записи законов изменяется. Иначе устанавливается связь и между однородными электрическими величинами. Так, при последовательном соединении в постоянном токе общее сопротивление было равно арифметической сумме сопротивлений, в переменном токе берется уже геометрическая сумма R, ХL ХC. А токи, сходящиеся в узле, так же как и напряжения, действующие на элементах контура и мощности на этих сопротивлениях, суммируются геометрически, т. е. складываются соответствующие векторы.
В этом случае электротехническая задача может быть сведена к задаче геометрической.
Такой метод требует точного построения векторной диаграммы, что невозможно без проведения предварительных расчетов токов и напряжений приемника.