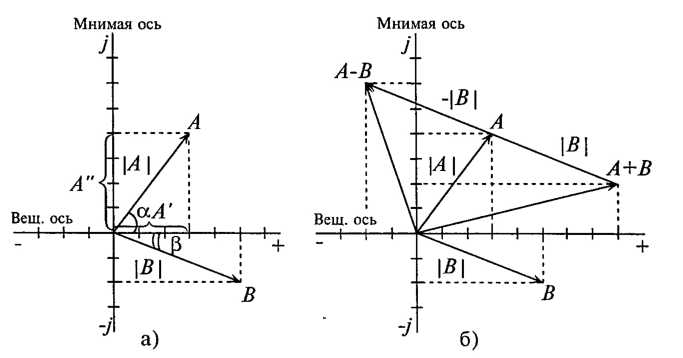
Пример 1 Метод узловых и контурных уравнений, составленных по законам Кирхгофа

Дата: 2025-05-01; Просмотры: 4

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Решение

1. На схеме произвольно показываем направления токов ветвей.

2. В задаче три неизвестных тока, для их нахождения необходимо
составить систему из трех уравнений.

Первое уравнение составим для узловой точки С по первому закону Кирхгофа:

I₁ +I₂ –I₃ =0

второе уравнение составим для контура АСDВА по второму закону Кирхгофа; направление обхода контура примем «по часовой стрелке»

Е₁—Е₂ =I₁ (R₁+R₀₁)— I₂(R₂+R₀₂);

третье уравнение составим для контура СКNDС но второму закону Кирхгофа; направление обхода контура примем «по часовой стрелке»:

Е₂= I₂(R₂+R₀₂) +I₃R₃.

3. Подставляем исходные данные в полученную систему из трех уравнений и находим значения токов ветвей:

Из второго уравнения получаем:

70=10 I₁ – 20 I₂;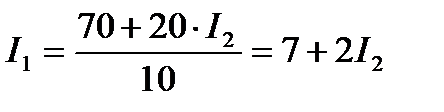

Из третьего уравнения получаем:

80=20I₂ + 25I₃;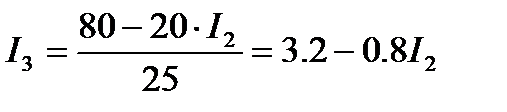

Подставляем выражения I₁ и I₃ в первое уравнение и находим ток I₂:

I₂+7 + 2 I₂ - 3,2 + 0,8 I₂ = 0; 3,8 I₂ = - 3,8; I ₂ = -1А

Определяем токи I₁ и I₃:

I₁ = 7+2 • (-1 )=5 А; I₃=3,2—0,8 (- 1) =4 А.

Проверка по первому закону Кирхгофа: I₁ + I₂ - I₃=0; 5-1- 4 = 0.

Ток I₂ получился отрицательным, это значит, что первоначально произвольно принятое направление тока I₂ от точки D к точке С оказалось неверным и должно быть изменено на противоположное. При этом ток I₂ будет направлен против направления Э.Д.С. Е₂, следовательно, источник с Э.Д.С. Е₂ находится в режиме потребителя (например, заряд батареи аккумуляторов)

Пример 2 Метод контурных токов

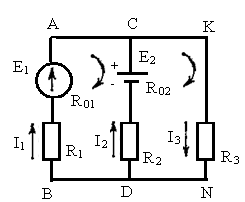
Рисунок 4 - Электрическая схема

Решение

1. На схеме произвольно показываем направление токов ветвей.

2. Намечаем два независимых контура и указываем направление контурных токов « по часовой стрелке»

3. Определяем Э.Д.С. каждого контура:

Е _I = Е₁ – Е₂ = 150 -80 = 70 В

Е _II = Е₂ = 80 В

4. Определяем собственные и общие сопротивления контуров:

- собственные сопротивления

R₁₁ = R₁ + R₀₁ + R₀₂ + R₂ = 9 + 1 + 0,5 + 19,5 = 30 Ом

R₂₂ = R₂ + R₀₂ + R₃ = 19,5 + 0,5 + 25 = 45 Ом

- общие сопротивления

R₁₂ = R₂₁ = R₂ + R₀₂ = 19,5 + 0.5 = 20 Ом

5. Составляем уравнения:

I _I R₁₁ – I _II R₁₂ = E _I

I _II R₂₂ – I _I R₂₁ = E _II

6. Подставляем данные, полученные в пунктах 3, 4 и решаем систему уравнений методом подстановки или любым другим методом.

I _I 30 – I _II 20 = 70 (1) (* 2)

- I _I 20 + I _II 45 = 80 (2) (* 3)

60 I _I – 40 I _II = 140 (3)

- 60 I _I + 135 I _II = 240 (4)

_______________________________

95 I _II = 380

I _II = 4 A

7. Подставляем значение I _II в формулу (1) и определяем ток I _I.

30 I _I – 4 * 20 = 70

I _I = 150 / 30

I _I = 5 A

8. Определяем действительные токи в ветвях, исходя из условия, что действительный ток , совпадающий по направлению с контурным током берется со знаком «+», и наоборот, ток в ветви не совпадающий с контурным током берется со знаком «-».

I₁ = I _I = 5 A

I₂ = I _II– I _I = 4 – 5 = -1 A

I₃= I _II =4A

Пример 3 Метод узлового напряжения

Решение

1. Проводимости ветвей

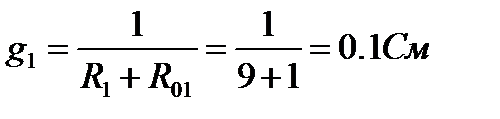
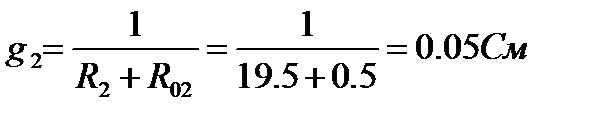
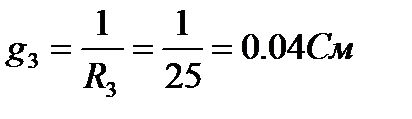
2. Узловое напряжение

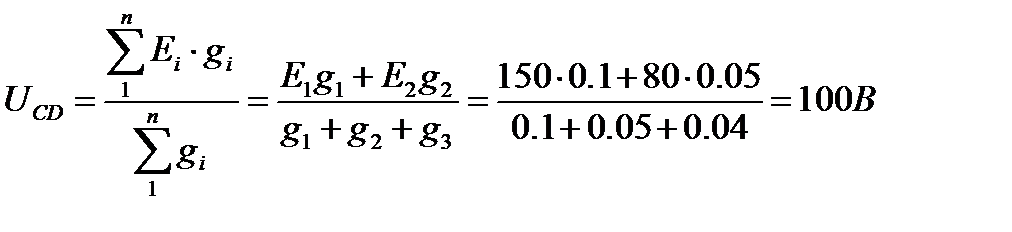
3. Токи в ветвях

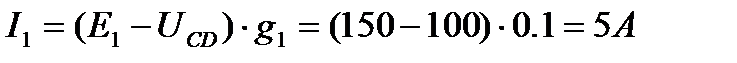
Направление тока I₁ совпадает с направлением Э.Д.С. Е₁. Ток I₁ направлен от узла C к узлу D.

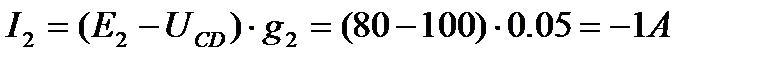
Направление тока I₂ противоположно направлению Э.Д.С. Е₂ (режим потребителя). Ток I₂ направлен от узла C к узлу D.

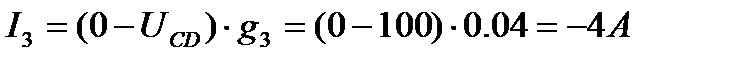
Ток I₃ направлен от узла C к узлу D. Покажем направление токов на заданной схеме (рисунок 5)

4. Составим уравнение баланса мощностей цепи.

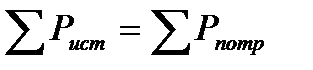
Для данной цепи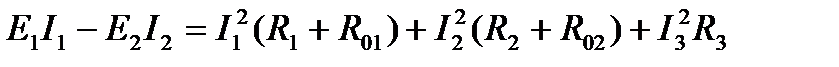

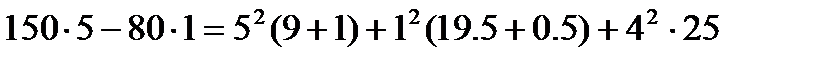
670 Вт = 670 Вт

Методические указания к решению задачи 2

Эти задачи относятся к теме «Символический метод расчета электрических цепей переменного тока».

КРАТКИЕ СВЕДЕНИЯ

Символический метод нашел широкое применение для расчета сложных цепей переменного тока.

Символический метод расчета основан на использовании комплексных чисел.

Комплексное число 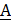состоит из вещественной А' и мнимой А" частей, т. е. 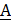= А' + jA ".

Комплексное число на комплексной плоскости можно представить вектором. Проекция вектора на вещественную ось (ось абсцисс) соответствует вещественной части комплексного числа А' рис. 5 а). Проекция вектора на мнимую ось j (ось ординат) соответствует коэффициенту при мнимой единице А". Мнимая единица j представляет собой поворотный множитель, умножение на который означает поворот вектора на 90° против часовой стрелки, т.е. в положительном направлении. Мнимая единица 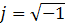. Тогда .

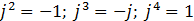Рисунок 5 - Вращающийся вектор на комплексной плоскости