Метод рівних та найменших відносних відхилень
Розв’язок
1.Задамо значення параметрів згідно варіанту завдання :
a1 = 2;
a2 = 2;
a3 = 3;
b1 = 2;
b2 = 2;
b3 = 1;
d1 = 8;
d2 = 3;
d3 = 1;
h11 = 6;
h12 = 11;
h13 = 19;
h21 = 12;
h22 = 8;
h23 = 11;
h31 = 1;
h32 = 1;
h33 = 10;
H1 = 860;
H2 = 790;
H3 = 820;
L1 = 10;
L2 = 10;
L3 = 20;
2. Використовуючи функцію “linprog” системи комп’ютерної математики MATLAB, обчислимо екстремум кожного окремого критерію на заданій ОДР G(! Пам’ятаємо, що функція “ linprog ” обчислює мінімум критерія):
>> A=[h11 h12 h13;h21 h22 h23;h31 h32 h33]
>> b=[H1;H2;H3]
>> lb=[ L1;L2;L3]
>> C1=[a1 a2 a3]
>> C2=[b1 b2 b3]
>> C3=[d1 d2 d3]
A =
6 11 19
12 8 11
1 1 10
b =
860
790
820
lb =
10
10
20
C1 =
2 2 3
C2 =
2 2 1
C3 =
8 3 1
>> [Xw1,minusW1,flag]=linprog((-1)*C1,A,b,[],[],lb,[])
W1max = -minusW1
[Xw2,minusW2,flag]=linprog( (-1)* C2,A,b,[],[],lb,[])
W2max = -minusW2
[Xw3,minusW3,flag]=linprog((-1)*C3,A,b,[],[],lb,[])
W3max=-minusW3
Optimization terminated.
Xw1 =
28.9286
27.8571
20.0000
minusW1 =
-173.5714
flag =
1
W1max =
173.5714
Optimization terminated.
Xw2 =
28.9286
27.8571
20.0000
minusW2 =
-133.5714
flag =
1
W2max =
133.5714
Optimization terminated.
Xw3 =
40.8333
10.0000
20.0000
minusW3 =
-376.6667
flag =
1
W3max =
376.6667
3. Методи розв’язання задач багатокритеріальної (векторної) оптимізації.
3.1. Метод рівних і найменших відносних відхилень
3.1.1. Побудуємо додаткові до ОДР G обмеження – рівності на основі співвідношень :
(W1max - a1*x1 - a2*x2 - a3*x3 )/W1max = 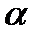 2 *(W2max - b1*x1 - b2*x2 - b3*x3)/W2max;
2 *(W2max - b1*x1 - b2*x2 - b3*x3)/W2max;
(W1max - a1*x1 - a2*x2 - a3*x3 )/W1max = 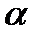 3*(W3max - d1*x1 - d2*x2 - d3*x3 )/W3max;
3*(W3max - d1*x1 - d2*x2 - d3*x3 )/W3max;
Для отримання стійкої обчислювальної процедури задамо точність виконання обмежень - рівностей:
-D21 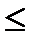 (W1max - a1*x1 - a2*x2 - a3*x3 )/W1max -
(W1max - a1*x1 - a2*x2 - a3*x3 )/W1max - 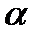 2 *(W2max - b1*x1 - b2*x2 - b3*x3)/W2max
2 *(W2max - b1*x1 - b2*x2 - b3*x3)/W2max 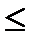 D21
D21
або
(-1)*(alfa2*(W2max )^(-1)*C2-(W1max )^(-1)*C1) 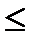 D21+1-alfa2;
D21+1-alfa2;
;alfa2*(W2max )^(-1)*C2-(W1max )^(-1)*C1 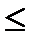 D21-1+alfa2;
D21-1+alfa2;
та
-D31 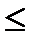 (W1max - a1*x1 - a2*x2 - a3*x3 )/W1max -
(W1max - a1*x1 - a2*x2 - a3*x3 )/W1max - 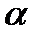
3*(W3max - d1*x1 - d2*x2 - d3*x3 )/W3max 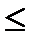 D31
D31
або
(-1)*(alfa3*(W3max )^(-1)*C3-(W1max )^(-1)*C1) 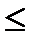 D31+1-alfa3;
D31+1-alfa3;
;alfa3*(W3max )^(-1)*C3-(W1max )^(-1)*C1 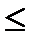 D31-1+alfa3,
D31-1+alfa3,
де D21 та D31 - малі додатні числа.
3.1.2. Критерій та мета оптимізації:
C1*X 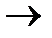 max ,
max ,
3.1.3.Розв’язок задачі у форматі системи комп’ютерної математики MATLAB
>> alfa2=0.5 ;
>> alfa 3=0.5 ;
D 21= 0. 1 ;
D 31= 0. 1 ;
AA=[(-1)*(alfa 2*( W 2 max )^(-1)* C 2-( W 1 max )^(-1)* C 1); alfa 2*( W 2 max )^(-1)* C 2-( W 1 max )^(-1)* C 1; (-1)*( alfa 3*( W 3 max )^(-1)* C 3-( W 1 max )^(-1)* C 1); alfa 3*( W 3 max )^(-1)* C 3-( W 1 max )^(-1)* C 1; A ]
AA =
0.0040 0.0040 0.0135
-0.0040 -0.0040 -0.0135
0.0009 0.0075 0.0160
-0.0009 -0.0075 -0.0160
6.0000 11.0000 19.0000
12.0000 8.0000 11.0000
1.0000 1.0000 10.0000
Bb = [D21+1-alfa2;D21-1+alfa2; D31+1-alfa3;D31-1+alfa3;b]
Bb =
0.6000
-0.4000
0.6000
-0.4000
860.0000
790.0000
820.0000
[Xw1,minusW1,flag]=linprog((-1)*C1,AA,Bb,[],[],lb,[])
Optimization terminated.
Xw1 =
28.9286
27.8571
20.0000
minusW1 =
-173.5714
flag =
1
Метод мінімаксу
Розв’язок
1.Задамо значення параметрів згідно варіанту завдання :
a1 = 2;
a2 = 2;
a3 = 3;
b1 = 2;
b2 = 2;
b3 = 1;
d1 = 8;
d2 = 3;
d3 = 1;
h11 = 6;
h12 = 11;
h13 = 19;
h21 = 12;
h22 = 8;
h23 = 11;
h31 = 1;
h32 = 1;
h33 = 10;
H1 = 860;
H2 = 790;
H3 = 820;
L1 = 10;
L2 = 10;
L3 = 20;
2. Використовуючи функцію “linprog” системи комп’ютерної математики MATLAB, обчислимо екстремум кожного окремого критерію на заданій ОДР G(! Пам’ятаємо, що функція “ linprog ” обчислює мінімум критерія):
>> A=[h11 h12 h13;h21 h22 h23;h31 h32 h33]
>> b=[H1;H2;H3]
>> lb=[ L1;L2;L3]
>> C1=[a1 a2 a3]
>> C2=[b1 b2 b3]
>> C3=[d1 d2 d3]
A =
6 11 19
12 8 11
1 1 10
b =
860
790
820
lb =
10
10
20
C1 =
2 2 3
C2 =
2 2 1
C3 =
8 3 1
>> [Xw1,minusW1,flag]=linprog((-1)*C1,A,b,[],[],lb,[])
W1max = -minusW1
[Xw2,minusW2,flag]=linprog( (-1)* C2,A,b,[],[],lb,[])
W2max = -minusW2
[Xw3,minusW3,flag]=linprog((-1)*C3,A,b,[],[],lb,[])
W3max=-minusW3
Optimization terminated.
Xw1 =
28.9286
27.8571
20.0000
minusW1 =
-173.5714
flag =
1
W1max =
173.5714
Optimization terminated.
Xw2 =
28.9286
27.8571
20.0000
minusW2 =
-133.5714
flag =
1
W2max =
133.5714
Optimization terminated.
Xw3 =
40.8333
10.0000
20.0000
minusW3 =
-376.6667
flag =
1
W3max =
376.6667
3. Методи розв’язання задач багатокритеріальної (векторної) оптимізації.
3.1. Метод мінімаксу
3.1.1. Побудуємо додаткові до ОДР G обмеження – нерівності на основі співвідношень :
(W1max - a1*x1 - a2*x2 - a3*x3 )/W1max 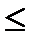
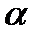 1*x4 ;
1*x4 ;
(W2max - b1*x1 - b2*x2 - b3*x3)/W2max 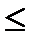
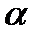 2 *x4 ;
2 *x4 ;
(W3max - d1*x1 - d2*x2 - d3*x3 )/W3max 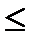
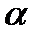 3*x4 ,
3*x4 ,
де 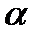 1+
1+ 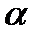 2+
2+ 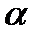 3 = 1
3 = 1
або
-(W1max )^(-1)*C1*X - 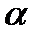 1*x4
1*x4 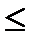 -1;
-1;
-(W2max )^(-1)*C2*X - 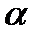 2*x4
2*x4 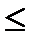 -1;
-1;
-(W3max )^(-1)*C3*X - 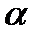 3*x4
3*x4 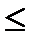 -1;
-1;
або
[-(W1max )^(-1)*C1 - 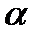 1]*[X;x4 ]
1]*[X;x4 ] 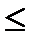 -1;
-1;
[-(W2max )^(-1)*C2 - 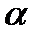 2]*[X;x4 ]
2]*[X;x4 ] 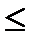 -1;
-1;
[-(W3max )^(-1)*C3 - 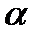 3]*[X;x4 ]
3]*[X;x4 ] 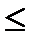 -1;
-1;
3.1.2. Критерій та мета оптимізації:
x4 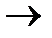 max
max
або
[0 0 0 1]*X 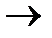 max .
max .
3.1.3.Розв’язок задачі у форматі системи комп’ютерної математики MATLAB
alfa1=0.5 ;
alfa2=0.25 ;
alfa3=0.25 ;
AA=[[-(W1max )^(-1)*C1 -alfa1];[-(W2max )^(-1)*C2 -alfa2];[-(W3max )^(-1)*C3 -alfa3];A [0;0;0]]
AA =
-0.0115 -0.0115 -0.0173 -0.5000
-0.0150 -0.0150 -0.0075 -0.2500
-0.0212 -0.0080 -0.0027 -0.2500
6.0000 11.0000 19.0000 0
12.0000 8.0000 11.0000 0
1.0000 1.0000 10.0000 0
Bb = [-1;-1;-1;b]
Bb =
-1
-1
-1
860
790
820
[XX4,X4,flag]=linprog([0 0 0 1],AA,Bb,[],[],[lb;0],[])
Optimization terminated.
XX4 =
35.5214
17.9678
20.0000
0.1974
X4 =
0.1974
flag =
1








