Метод цільового програмування
Національний технічний університет України
Київський політехнічний інститут
Інститут телекомунікаційних систем
Домашня контрольна робота
дисципліни «Теорія прийняття рішень та системний аналіз»
на тему «Застосування методів векторної оптимізації для розв’язування задач підвищення ефективності ТКС»
Варіант 6
Виконала: ст..гр.ТЗ-41м
Москвитіна А.О.
Прийняв: Лисенко О.І.
Київ 2014
Методика розрахунків до питання 1
Постановка задачі
Розв’язати задачу багатокритеріальної(векторної) оптимізації:
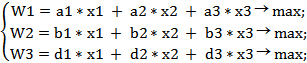
де ОДР G задана нерівностями
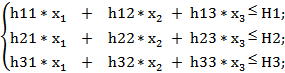
l1 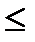 x1;
x1;
l2 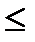 x2;
x2;
l3 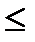 x3;
x3;
критерії упорядковані за рівнем важливості ( індекс “1” відповідає найважливішому критерію), МЕТОДОМ: ідеальної точки; цільового програмування (р=2; 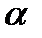 1=0.5,
1=0.5, 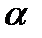 2=0.3,
2=0.3, 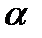 3=0.2); послідовних поступок; рівних та найменших відносних відхилень(
3=0.2); послідовних поступок; рівних та найменших відносних відхилень( 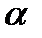 1=1,
1=1, 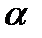 2=0.5,
2=0.5, 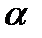 3=0.5; обчислення додаткових обмежень – рівностей виконати із точністю D12=D13=0.1); мінімаксу (
3=0.5; обчислення додаткових обмежень – рівностей виконати із точністю D12=D13=0.1); мінімаксу ( 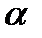 1=0.5,
1=0.5, 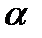 2=0.25,
2=0.25, 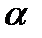 3=0.25).
3=0.25).
Таблиця 1. Вихідні данні
| Варіант | a1 | a2 | a3 | b1 | b2 | b3 | d1 | d2 | d3 | H1 | H2 | H3 |
| 1,7,13,19,25 | 1 | 2 | 3 | 4 | 4 | 4 | 8 | 3 | 1 | 840 | 770 | 800 |
| 2,8,14,20,26 | 1 | 2 | 3 | 3 | 2 | 1 | 8 | 3 | 1 | 830 | 760 | 790 |
| 3,9,15,21,27 | 3 | 2 | 1 | 1 | 2 | 1 | 8 | 3 | 1 | 820 | 750 | 780 |
| 4,10,16,22,28 | 3 | 2 | 1 | 1 | 2 | 1 | 8 | 3 | 1 | 820 | 750 | 780 |
| 5,11,17,23,29 | 2 | 2 | 1 | 1 | 2 | 1 | 8 | 3 | 1 | 850 | 780 | 810 |
| 6,12,18,24,30 | 2 | 2 | 3 | 2 | 2 | 1 | 8 | 3 | 1 | 860 | 790 | 820 |
Таблиця 1(продовження). Вихідні данні
| h11 | h12 | h13 | h21 | h22 | h23 | h31 | h32 | h33 | l1 | l2 | l3 |
| 7 | 12 | 20 | 11 | 7 | 10 | 1 | 1 | 10 | 10 | 10 | 10 |
| 7 | 12 | 20 | 11 | 7 | 10 | 1 | 1 | 10 | 10 | 10 | 10 |
| 7 | 12 | 20 | 11 | 7 | 10 | 1 | 1 | 10 | 10 | 10 | 10 |
| 6 | 11 | 19 | 12 | 8 | 11 | 1 | 1 | 10 | 10 | 10 | 10 |
| 6 | 11 | 19 | 12 | 8 | 11 | 1 | 1 | 10 | 10 | 10 | 20 |
| 6 | 11 | 19 | 12 | 8 | 11 | 1 | 1 | 10 | 10 | 10 | 20 |
Метод ідеальної точки
Розв’язок
1.Задамо значення параметрів згідно 6 варіанту завдання:
a1 = 2;
a2 = 2;
a3 = 3;
b1 = 2;
b2 = 2;
b3 = 1;
d1 = 8;
d2 = 3;
d3 = 1;
h11 = 6;
h12 = 11;
h13 = 19;
h21 = 12;
h22 = 8;
h23 = 11;
h31 = 1;
h32 = 1;
h33 = 10;
H1 = 860;
H2 = 790;
H3 = 820;
l1 = 10;
l2 = 10;
l3 = 20;
Таким чином, маємо:
W1= 2x1 + 2x2 + 3x3 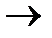 max;
max;
W2= 2x1 + 2x2 + x3 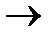 max;
max;
W3= 8x1 + 3x2 + x3 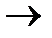 max;
max;
де ОДР G задана нерівностями
6x1 + 11x2 + 19x3 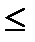 860;
860;
12x1 + 8x2 + 11x3 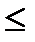 790;
790;
x1 + x2 + x3 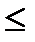 820;
820;
l1 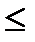 x1;
x1;
l2 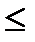 x2;
x2;
l3 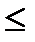 x3;
x3;
2. Використовуючи функцію “linprog” системи комп’ютерної математики MATLAB, обчислимо екстремум кожного окремого критерію на заданій ОДР G(! Пам’ятаємо, що функція “ linprog ” обчислює мінімум критерія):
>> A=[h11 h12 h13;h21 h22 h23;h31 h32 h33]
>> b=[H1;H2;H3]
>> lb=[ l1;l2;l3]
>> C1=[a1 a2 a3]
>> C2=[b1 b2 b3]
>> C3=[d1 d2 d3]
Згідно варіанту маємо:
A =
6 11 19
12 8 11
1 1 10
b =
860
790
820
lb =
10
10
20
C1 =
2 2 3
C2 =
2 2 1
C3 =
8 3 1
>> [Xw1,minusW1,flag]=linprog((-1)*C1,A,b,[],[],lb,[])
W1max = -minusW1
[Xw2,minusW2,flag]=linprog( (-1)* C2,A,b,[],[],lb,[])
W2max = -minusW2
[Xw3,minusW3,flag]=linprog((-1)*C3,A,b,[],[],lb,[])
W3max=-minusW3
Optimization terminated.
Xw1 =
28.9286
27.8571
20.0000
minusW1 =
-173.5714
flag =
1
W1max =
173.5714
Optimization terminated.
Xw2 =
28.9286
27.8571
20.0000
minusW2 =
-133.5714
flag =
1
W2max =
133.5714
Optimization terminated.
Xw3 =
40.8333
10.0000
20.0000
minusW3 =
-376.6667
flag =
1
W3max =
376.6667
3. Методи розв’язання задач багатокритеріальної (векторної) оптимізації.
3.1. Метод ідеальної точки.
3.1.1. Знайдемо рівняння площини da*w1+db*w2+dc*w3 = dd, яка задає положення множини Парето, в системі координат W1W2W3O, де
“dd” – визначник матриці d, “da” - визначник матриці a,
“db” - визначник матриці b, “dc ”- визначник матриці c:
W11=W1max;
W12=C2*Xw1;
W13=C3*Xw1;
W21=C1*Xw2;
W22=W2max ;
W23=C3*Xw2;
W31=C1*Xw3;
W32=C2*Xw3;
W33=W3max;
d=[W11 W12 W13;
W21 W22 W23;
W31 W32 W33] ;
dd=det(d)
d =
173.5714 133.5714 335.0000
173.5714 133.5714 335.0000
161.6667 121.6667 376.6667
dd =
8.5292e-004
a=[W12 W13 1;
W22 W23 1;
W32 W33 1] ;
da=det(a)
a =
133.5714 335.0000 1.0000
133.5714 335.0000 1.0000
121.6667 376.6667 1.0000
da =
4.1721e-006
b=[W13 W11 1;
W23 W21 1;
W33 W31 1] ;
db=det(b)
b =
335.0000 173.5714 1.0000
335.0000 173.5714 1.0000
376.6667 161.6667 1.0000
db =
-1.1800e-006
c= [W11 W12 1;
W21 W22 1;
W31 W32 1] ;
dc=det(c)
c =
173.5714 133.5714 1.0000
173.5714 133.5714 1.0000
161.6667 121.6667 1.0000
dc =
8.5487e-007
3.1.2. Рівняння прямої, що проходить через “точку утопії” (W11;W12;W13) в системі координат W1W2W3O перпендикулярно до площини da*w1+db*w2+dc*w3 = dd має вигляд:
(w1-W11)/da = (w2-W22)/db = (w3-W33)/dc.
3.1.3. Знайдемо компромісне рішення
Xkompromis=[x1kompromis x2kompromis x3kompromis]
в системі координат X1X2X3O, використовуючи точку компромісного рішення
Wkompromis=[Wkompromis1 Wkompromis2 Wkompromis3]
в площині Парето da∙w1+db∙w2+dc∙w3 = dd , яка найменше віддалена від точки утопії, шляхом розв’язання системи рівнянь:
da*w1+db*w2+dc*w3 = dd ,
(w1-W11)/da = (w2-W22)/db,
(w1-W11)/da = (w3-W33)/dc
або
[da db dc;
db (-1)*da 0;
dc 0 (-1)* da ] =[dd;db*W11-da*W22;dc*W11-da*W33].
Остаточно маємо
Wkompromis=inv([ da db dc;
db (-1)*da 0;
dc 0 (-1)* da ])*[dd;db*W11-da*W22;dc*W11-da*W33]
Xkompromis=inv([C1;C2;C3])*Wkompromis
Wkompromis =
165.9620
135.7237
375.1075
Xkompromis =
35.8163
24.4860
15.1192
Метод цільового програмування
Розв’язок
1.Задамо значення параметрів згідно варіанту завдання :
a1 = 2;
a2 = 2;
a3 = 3;
b1 = 2;
b2 = 2;
b3 = 1;
d1 = 8;
d2 = 3;
d3 = 1;
h11 = 6;
h12 = 11;
h13 = 19;
h21 = 12;
h22 = 8;
h23 = 11;
h31 = 1;
h32 = 1;
h33 = 10;
H1 = 860;
H2 = 790;
H3 = 820;
L1 = 10;
L2 = 10;
L3 = 20;
2. Використовуючи функцію “linprog” системи комп’ютерної математики MATLAB, обчислимо екстремум кожного окремого критерію на заданій ОДР G(! Пам’ятаємо, що функція “ linprog ” обчислює мінімум критерія):
>> A=[h11 h12 h13;h21 h22 h23;h31 h32 h33]
>> b=[H1;H2;H3]
>> lb=[ L1;L2;L3]
>> C1=[a1 a2 a3]
>> C2=[b1 b2 b3]
>> C3=[d1 d2 d3]
A =
6 11 19
12 8 11
1 1 10
b =
860
790
820
lb =
10
10
20
C1 =
2 2 3
C2 =
2 2 1
C3 =
8 3 1
>> [Xw1,minusW1,flag]=linprog((-1)*C1,A,b,[],[],lb,[])
W1max = -minusW1
[Xw2,minusW2,flag]=linprog( (-1)* C2,A,b,[],[],lb,[])
W2max = -minusW2
[Xw3,minusW3,flag]=linprog((-1)*C3,A,b,[],[],lb,[])
W3max=-minusW3
Optimization terminated.
Xw1 =
28.9286
27.8571
20.0000
minusW1 =
-173.5714
flag =
1
W1max =
173.5714
Optimization terminated.
Xw2 =
28.9286
27.8571
20.0000
minusW2 =
-133.5714
flag =
1
W2max =
133.5714
Optimization terminated.
Xw3 =
40.8333
10.0000
20.0000
minusW3 =
-376.6667
flag =
1
W3max =
376.6667
3. Методи розв’язання задач багатокритеріальної (векторної) оптимізації.
3.1. Метод цільового компромісного програмування(MЦKП)
Згідно завданню: р=2; 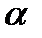 1=0.5,
1=0.5, 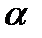 2=0.3,
2=0.3, 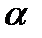 3=0.2.
3=0.2.
3.1.1. Побудова файл-функції: File_New_M-file
function CKP=myfunCKPmin(x,C1,C2,C3,W1max,W2max,W3max)
CKP=sqrt(0.5*((C1*[x(1);x(2);x(3)]-W1max)/W1max)^2+0.3*((C2*[x(1);x(2);x(3)]-W2max)/W2max)^2+0.2*((C3*[x(1);x(2);x(3)]-W3max)/W3max)^2);
Save as… myfunCKPmin
3.1.2. Пошук оптимального значення змінних із використанням функції fmincon системи комп’ютерної математики MATLAB:
Формат функції fmincon
[x,W,flag]=fmincon(@myfun,[x0],[A],[b],[Aeq],[beq],[lb],[ub],
@mynon,options,P1,P2,…)
[x,Dckp,flag]=fmincon(@myfunCKPmin,lb,A,b,[],[],lb,[],[],[],C1,C2,C3, W1max,W2max,W3max)
Warning: Trust-region-reflective algorithm does not solve this type of problem,
using active-set algorithm. You could also try the interior-point algorithm: set
the Algorithm option to 'interior-point' and rerun.
> In fmincon at 460
In CilProgram at 41
Local minimum possible. Constraints satisfied.
fmincon stopped because the predicted change in the objective function
is less than the default value of the function tolerance and constraints
were satisfied to within the default value of the constraint tolerance.
<stopping criteria details>
Active inequalities (to within options.TolCon = 1e-006):
lower upper ineqlin ineqnonlin
3 2
x =
33.3230
21.2655
20.0000
Dckp =
0.0402
flag =
5








