Приведение момента сопротивл-я
1. ТИПОВЫЕ СТАТИЧ-Е НАГРУЗКИ ЭП. МЕХ-Е ПП-СЫ ПРИ АКТ-М И РЕАК-НОМ Х-РЕ НАГРУЗКИ.
Кроме ЭМ-го м-нта на мех-скую часть ЭП-да действуют статические нагрузки, кот-е делятся на силы и моменты механ-х потерь и силы и моменты полезных нагрузок ИМ-ов:
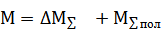 где 1ая составл-щая суммы явл-ся суммарными потерями в ЭД-ле и в ИМ-ме, а 2ая – суммарным приведённым м-нтом полезной нагрузки. По хар-ру взаимод-я с ЭП-дом разл-ся активные и реактивные силы и моменты.
где 1ая составл-щая суммы явл-ся суммарными потерями в ЭД-ле и в ИМ-ме, а 2ая – суммарным приведённым м-нтом полезной нагрузки. По хар-ру взаимод-я с ЭП-дом разл-ся активные и реактивные силы и моменты.
1. Вентилят-я нагрузка. Все эл-нты движутся с одинак-й скор-ю. На раб/колесе возникает сопр-е дв-ю, завис-щее от скорости. Общее сопр-е механизма:
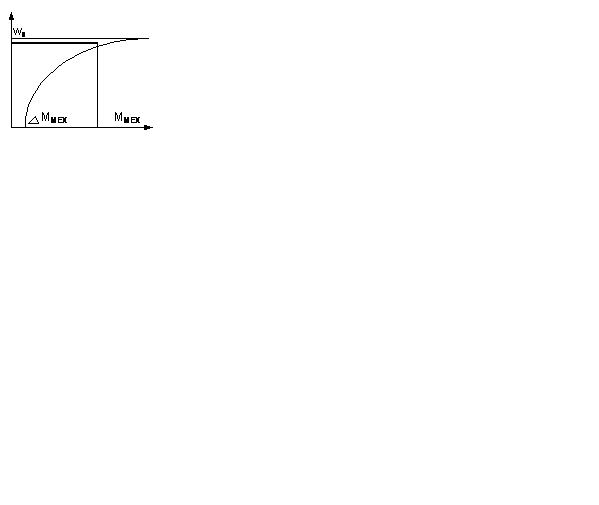

Где 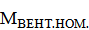 - номин-й момент вентилятора,
- номин-й момент вентилятора, 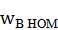 – номин-я скорость вентилятора. Если скорости не совпадают – преобр-е устр-ва – редукторы.
– номин-я скорость вентилятора. Если скорости не совпадают – преобр-е устр-ва – редукторы. 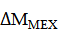 - мом-нт мех-х потерь на трение в подшипниках раб/колеса.
- мом-нт мех-х потерь на трение в подшипниках раб/колеса.
2. Механизмы с постоянной нагрузкой. Рассмотрим ЭП шпинделя токарного станка.
 Взаимод-е резца и заготовки возн-т сила резания:
Взаимод-е резца и заготовки возн-т сила резания: 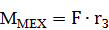 . В процессе обработки заготовки ост-ся пост-й м-нт и не зависит от w (снятие 1го слоя стружки, след-й слой=>др-е усилие. Момент зависит от радиуса заготовки.
. В процессе обработки заготовки ост-ся пост-й м-нт и не зависит от w (снятие 1го слоя стружки, след-й слой=>др-е усилие. Момент зависит от радиуса заготовки.
3. Мех-я х-ка симметрична относ-но начала координат.
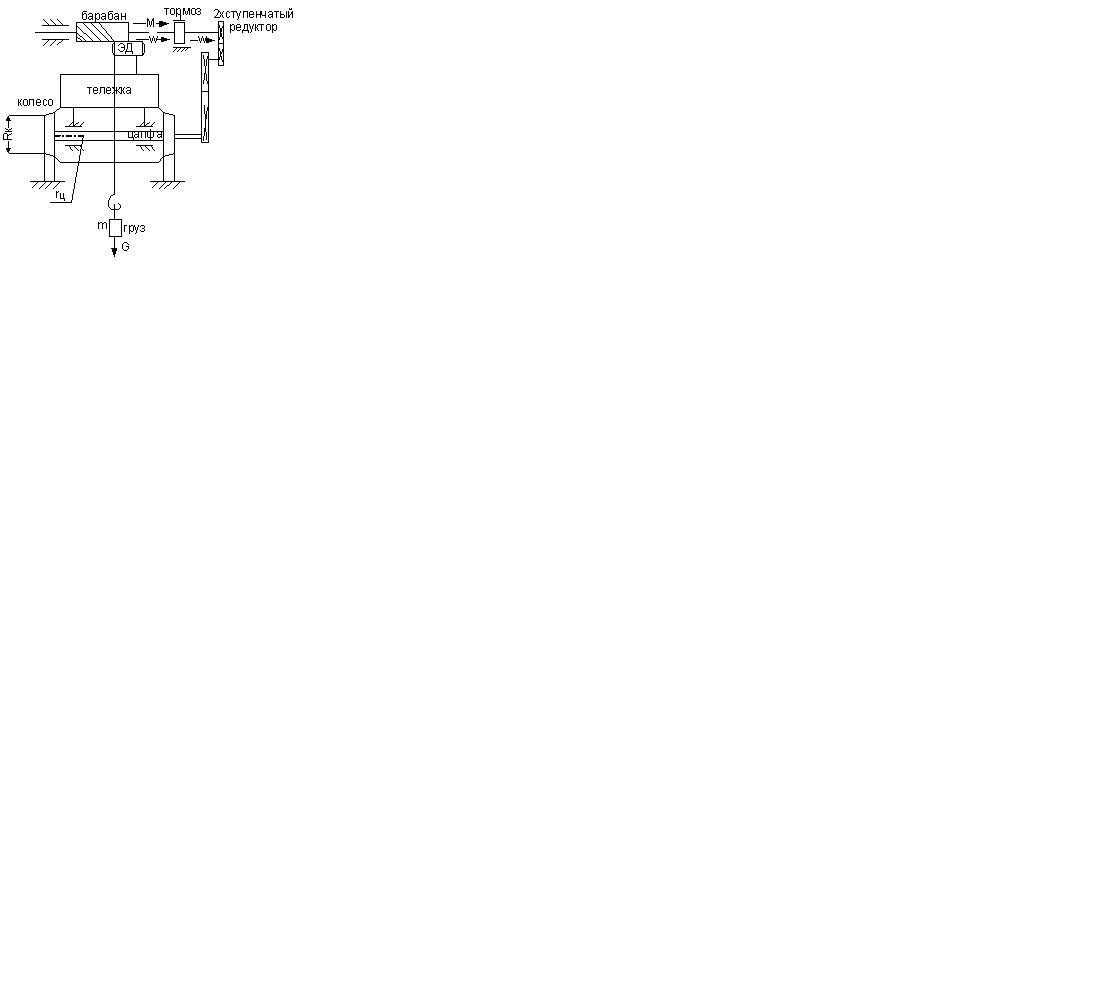
Напр., перемещение тележки мостового крана. Тележка перемещается по гор-му пути. ЭД
ч/з редуктор вращ-т колеса вед-е, преодолевая силу R-ния дв-ю тележки (Fмех), кот.возн-т из-за трения, скольж-я в цапфе и тр-я кач-я колес тележки по рельсам. Т.к. силы и м-нты пропорц-ны норм-му давлению, то:
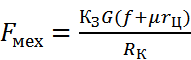 , где
, где 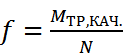 N – кол-во точек трения, а
N – кол-во точек трения, а 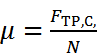 - сила тр-я скольжения. G – сила тяжести тележки.
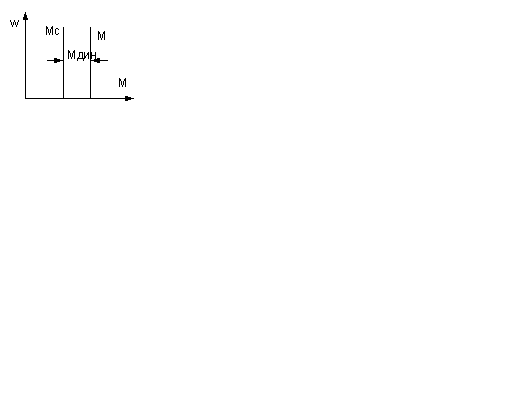
- сила тр-я скольжения. G – сила тяжести тележки. 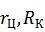 - радиус колес и цапф оси колес. Кз – коэф-т запаса, учит-т разного рода доп-е усилия (напр., трение реборт колес о бок-ю сторону рельса при перекосах и т.д.). Мех-я х-ка на рисунке. Она упрощена, т.к. сила сух-го трения неск-ко больше, чем сила трения продв-я. ЭП д.б. реверс-м=>х-ка симметр-на относ. начала корд-т.
- радиус колес и цапф оси колес. Кз – коэф-т запаса, учит-т разного рода доп-е усилия (напр., трение реборт колес о бок-ю сторону рельса при перекосах и т.д.). Мех-я х-ка на рисунке. Она упрощена, т.к. сила сух-го трения неск-ко больше, чем сила трения продв-я. ЭП д.б. реверс-м=>х-ка симметр-на относ. начала корд-т.
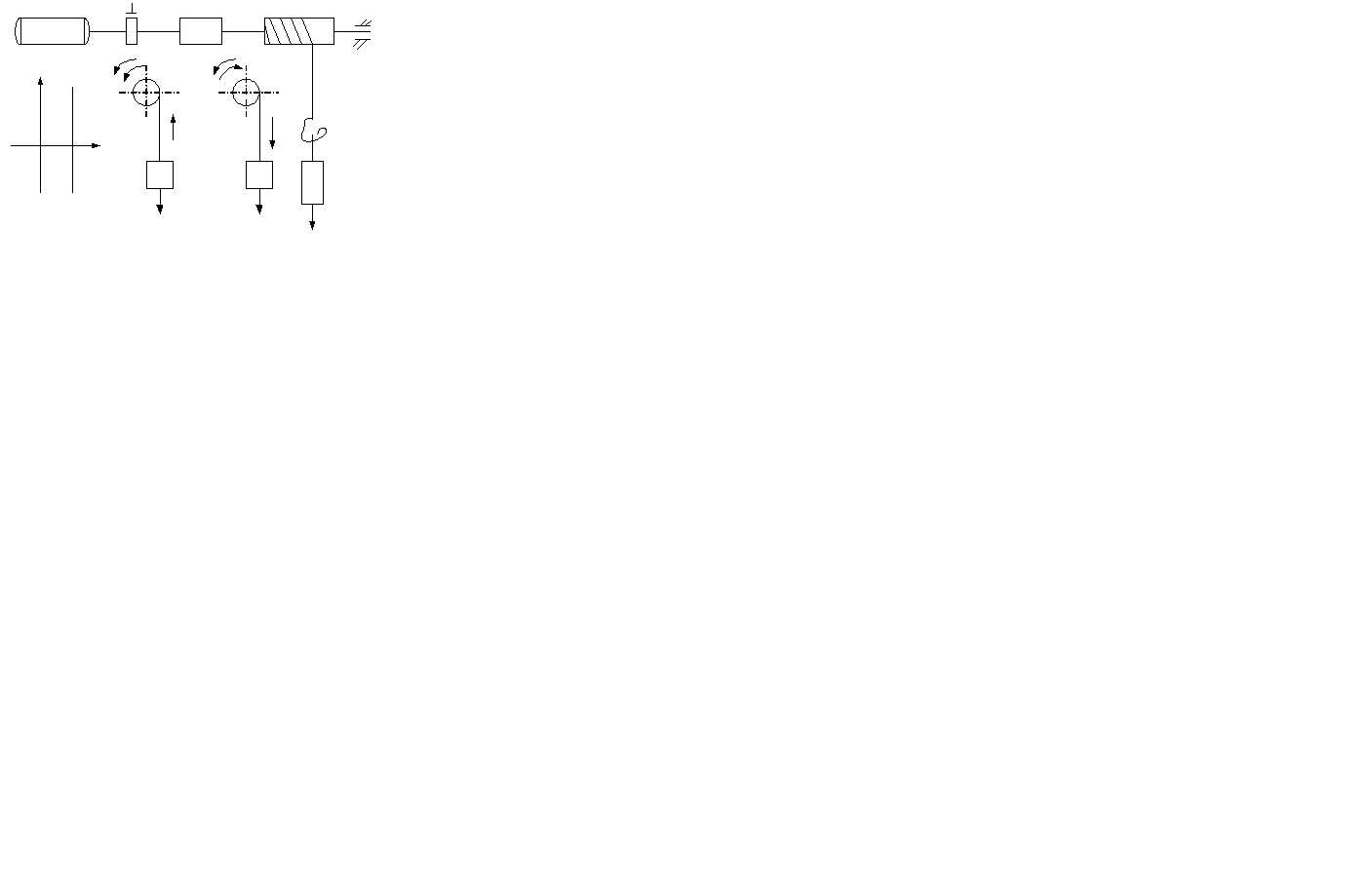 4. Мех-я х-ка, располож-я в правой части сист. координат I и IV квадранты. Причем М = const. ЭД-ль вращает барабан, кот-й перемещает груз. Нагрузкой явл-ся сила тяжести груза. Особен-сть этой нагрузки – она всегда напр-на в сторону спуска и не зависит от его перемещения. Подъем груза.
4. Мех-я х-ка, располож-я в правой части сист. координат I и IV квадранты. Причем М = const. ЭД-ль вращает барабан, кот-й перемещает груз. Нагрузкой явл-ся сила тяжести груза. Особен-сть этой нагрузки – она всегда напр-на в сторону спуска и не зависит от его перемещения. Подъем груза. 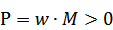 - ЭД
- ЭД
Явл-ся ист-ком (постав-щиком) мех-й энергии.
 Если груз надо опус-тить, то
Если груз надо опус-тить, то
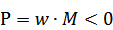
Т.е. ЭД явл-ся приемником мех-й эн-и, и режим исп-ся для тормож-я. 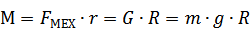 . Мс=[0, Мсном], т.е. до номин-й грузоподъемности G=Gном.
. Мс=[0, Мсном], т.е. до номин-й грузоподъемности G=Gном.
5. Мех-я х-ка мех-ма расположена в I и IV квадрантах. Напр., уравновеш-я система – есть противовес.
А) Пусть груз номин-й (предельно допус-й)G1НОМ>G2.
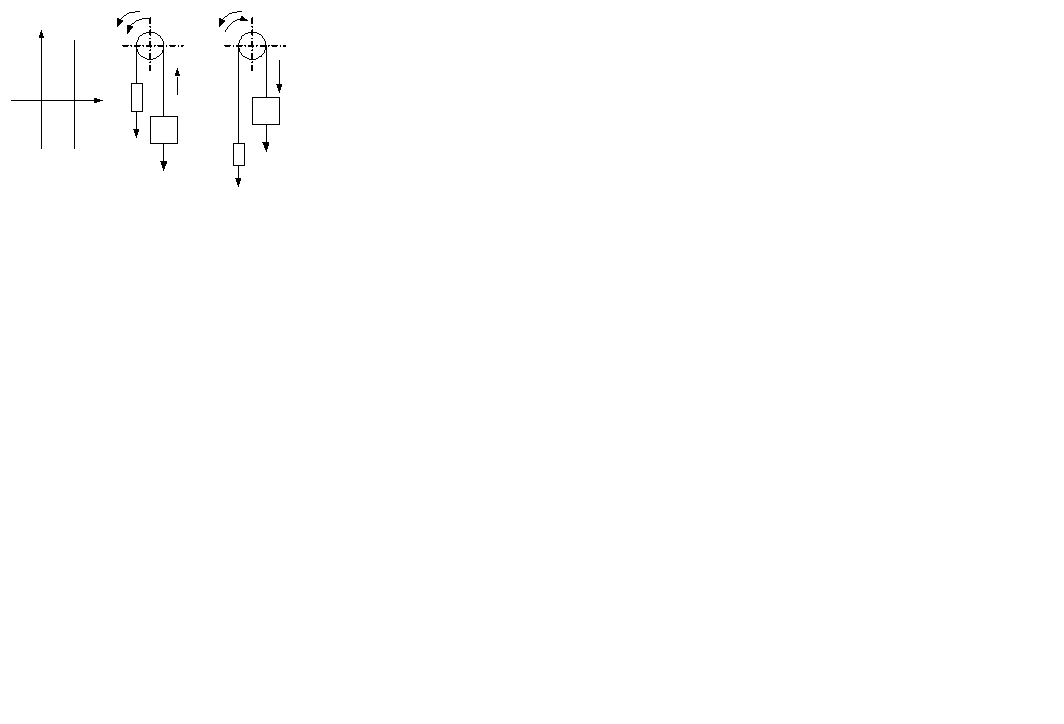
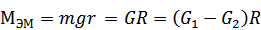
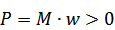
ЭД – приемник мех-й энергии.
Б) Спуск. ЭД раб-т в тормозном (генерат-м) р-ме, т.е.
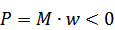
Активными силами и м-ми наз-ся силы и моменты, величина и направление которых не зависит от движения ЭПа; напр., силы и моменты, создаваемые перемещаемым по вертикали грузом.
 Реакт-е м-нты – м-нты, возник-е как р-ции на дв-е м-нт ЭД или на актив-й м-нт нагрузки. Всегда действ-т навстречу дв-ю. По х-ру зав-сти от скорости разл-т нагрузки типов сухого трения, вязкого трения, вентиляторного типа: a)
Реакт-е м-нты – м-нты, возник-е как р-ции на дв-е м-нт ЭД или на актив-й м-нт нагрузки. Всегда действ-т навстречу дв-ю. По х-ру зав-сти от скорости разл-т нагрузки типов сухого трения, вязкого трения, вентиляторного типа: a) 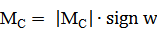
М-нты вязкого трения лин-но зав-т от скорости: 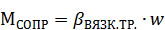 . В чистом виде встреч-ся редко, в осн-м в виде сух.тр.
. В чистом виде встреч-ся редко, в осн-м в виде сух.тр.
По х-ру влияния на мех/колеб-я:
- консерватив-е (при возд-и на сист. Не происх-т поглощ-е эн-и колеб-й. Не зав-т от скорости. Напр.,сила тяж. Работа за кол-е=0)
- диссепатив-е (м-нты, при возд-и кот.. на сист. Происх-т поглощ-е эн-и их колеб-я. Напр., вязкое трение, при изменении знака скорости измен-ся и знак м-нта, а мех-я мощ-сть 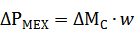 - сохр-т полож-й знак, что соотв-т поглоощ-ю эн-ю колеб-й).
- сохр-т полож-й знак, что соотв-т поглоощ-ю эн-ю колеб-й).
2. РАСЧЕТНЫЕ СХЕМЫ МЕХ-Й ЧАСТИ ЭП-ДА. ПРИВЕДЕНИЕ М-НТА СОПРОТИВЛЕНИЯ, М-НТА ИНЕРЦИИ, ЖЕСТКОСТИ К ВАЛУ ДВ-ЛЯ.
Осн-я задача ЭП – привед-е в дв-е произв-х мех-в и упр-е их дв-м для вып-я технол-х операций. Для расчета – кинем-я сх мез-ма, тех-е данные мех-ма, инф-я о технол-м процессе. Опр-ся – расчет-е (экв-е) сх. мех-й части, расчет пар-ров мех-й части ЭП, сост-ся М/М дв-я ЭП, рассчит-ся частотные х-ки мех-х ПП-в, проивз-ся их анализ.
Вращ-е дв-е: м-нт (Нм), угол поворота (φ), угловая скорость ( 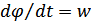 , рад/с), угловое ускор-е (
, рад/с), угловое ускор-е ( 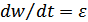 , рад/с2), рывок (
, рад/с2), рывок ( 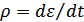 ).
).
Поступ-е дв-е: плечо, сила (перемещ-е), путь X (м), dx/dt проив-я пути, уск-е, рывок (r=da/dt).
Эл-нты ЭП, облад-е спос-ю накапливать эн-ю, разл-ся по ее виду: 1) кинем-я эн-я. Хар-ся вращ-е дв-е - м-нт инерции (J = кг/м2). Поступ-е – массой.
2) вращ-ся мех-мы накпл-т потенц-ю эн-ю – упр-е эл-нты, деформация кот подчин-ся з-ном Гука. Хар-ся коэф. Жесткости. Кручение: 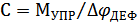 (Н/м*рад). При поступ-м дв-и (сжатие или растяж-е)
(Н/м*рад). При поступ-м дв-и (сжатие или растяж-е) 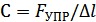 . Податливость
. Податливость 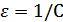 . (При нагружении валы, кино-ремниевые передачи, зубчатое зацепление, канаты и т.д. дефор-ся, т.к. они не абсол-но жесткие.
. (При нагружении валы, кино-ремниевые передачи, зубчатое зацепление, канаты и т.д. дефор-ся, т.к. они не абсол-но жесткие.
Приведение момента сопротивл-я
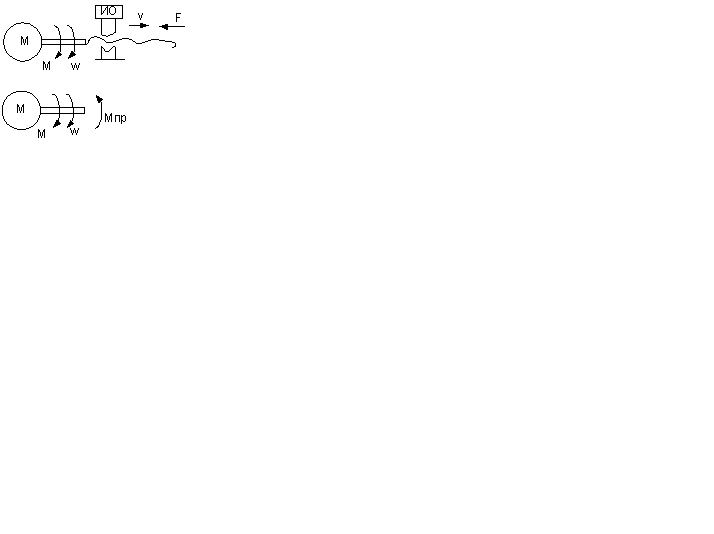
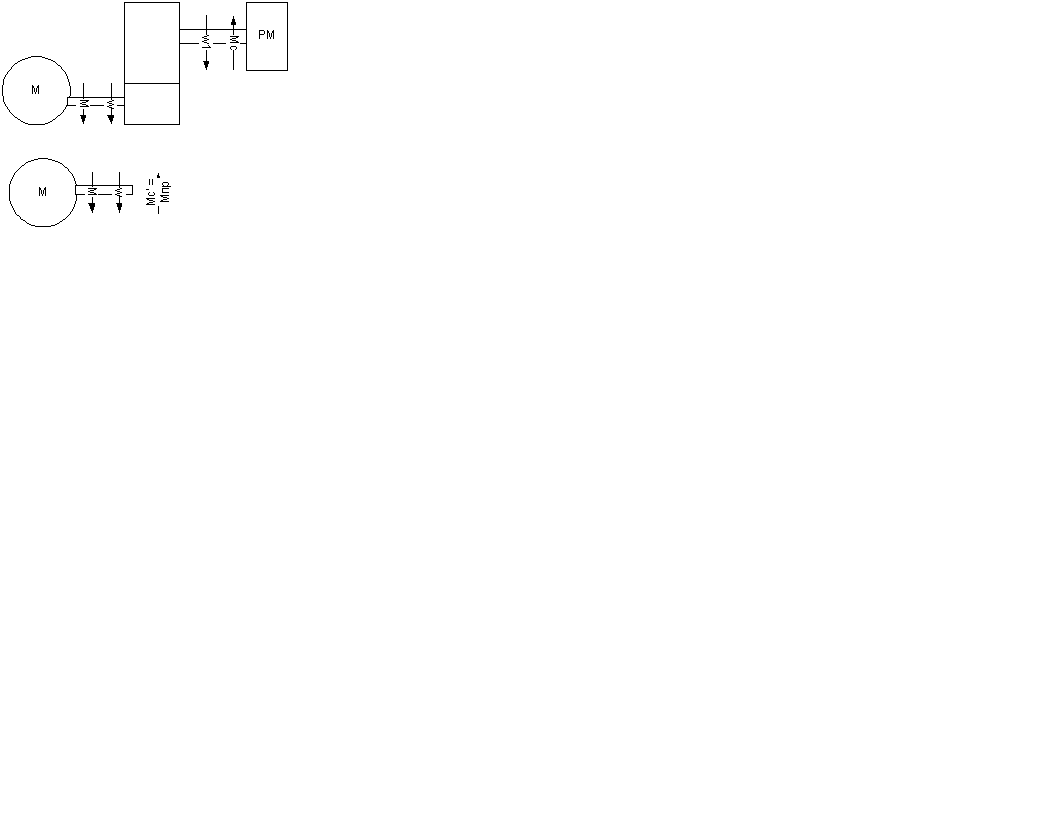 Усл-е привед-я: Т.к. мощ-сть расчет-й схемы и реал-й д.б. одинаковая, то усл-е равенства мощностей:
Усл-е привед-я: Т.к. мощ-сть расчет-й схемы и реал-й д.б. одинаковая, то усл-е равенства мощностей: 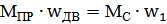 ;
; 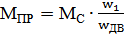 Где
Где 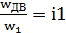 – передат-е соотношение.
– передат-е соотношение. 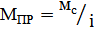 Если необх. учит-ть КПД редукторы (потери на трение), то
Если необх. учит-ть КПД редукторы (потери на трение), то 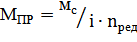 Если движение поступательное механич-й части:
Если движение поступательное механич-й части: 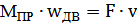
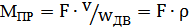 , где
, где 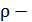 разность привед-я. Если необх. учесть потери на трение, то
разность привед-я. Если необх. учесть потери на трение, то 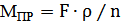 Привед-е м-нтов инерции. Иногда
Привед-е м-нтов инерции. Иногда 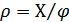 (лин-е перемещ-е, радиус поворота).
(лин-е перемещ-е, радиус поворота).
Привед-е м-нтов инерции.
Движущиеся части ЭП облад-т кинетич-й эн-й, численно равной работе, потрач-й на ее создание. М-нт приводит к инерции исходя из сохранения кинет-й энергии мех/сист. при переносе момента инерции на вал двигателя.
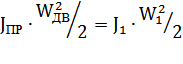
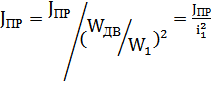
Для поступ-го: 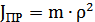 . (т.к. кинет-я эн-я
. (т.к. кинет-я эн-я 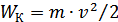 ) При привед-и м-тов инерции потери учит-ть не след-т, т.к. кинет-я энергия с потерями не связана. Общий м-нт инерции при жесткой связи дв-ля и механизма:
) При привед-и м-тов инерции потери учит-ть не след-т, т.к. кинет-я энергия с потерями не связана. Общий м-нт инерции при жесткой связи дв-ля и механизма: 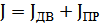
Приведение жесткости. Усл-е приведения: рав-ство потенц-х энергий реал-х и привд-х схем. 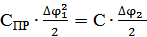 φ – угол закруч-я (поворота).
φ – угол закруч-я (поворота). 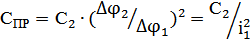
Для поступ-го движения: 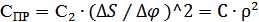
Опр-е м-нта инерции (расчетный и эксперим-й). 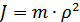
3. МЕХ-Я ЧАСТЬ ЭП-ДА КАК ОУ (НА ПРИМЕРЕ ДВУХМАС-ОЙ МОДЕЛИ).
 Мс2 – нагрузка, J1 – Рт+жестко св-е с ним эл-нты. М/М-ль и составл-я на ее основе схема явл-ся основой для анализа объекта. На основании схемы можно получить след-е ур-ния:
Мс2 – нагрузка, J1 – Рт+жестко св-е с ним эл-нты. М/М-ль и составл-я на ее основе схема явл-ся основой для анализа объекта. На основании схемы можно получить след-е ур-ния:
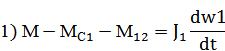
2) 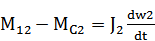
3) 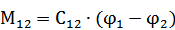
Из 3) получим: 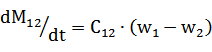 , где
, где 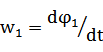 ,
, 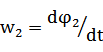 . Получ-я сист – М/М ДМС. На основании системы можно составить структ-ю схему:
. Получ-я сист – М/М ДМС. На основании системы можно составить структ-ю схему:
Сх. сост-т из 3-х интегр-х звеньев. Упр-щее возд-е – ЭМ-ный м-нт. Возм-е – М12. Перепишем сист-у ур-ний в операт-й форме:
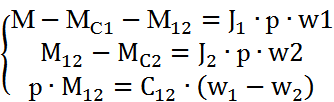
Опр-м Ww1w2(p) замкнутого контура:
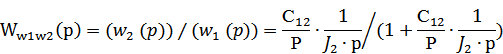
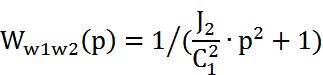
Опр-м 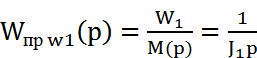
Передаточная функция ОС при w1:
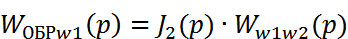
Тогда: 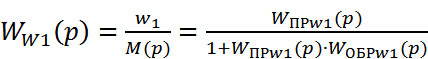
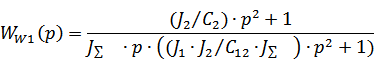
Закон изменения скорости нагрузки:
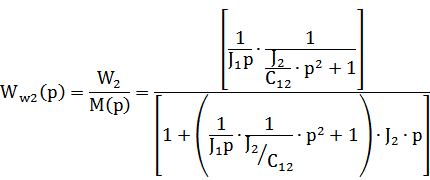
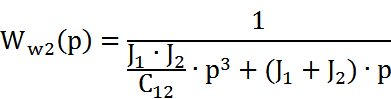
ХАУ: 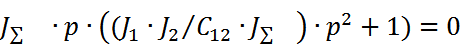
Р1=0. 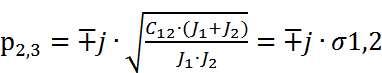 - где Ω1,2 – резонансная частота (частота своб-х колеб-й ДМ упр-й С). Т.е. ДМС п/с колеб-е звено. Ω1,2 – возм-но возн-е мех-го резонанса.
- где Ω1,2 – резонансная частота (частота своб-х колеб-й ДМ упр-й С). Т.е. ДМС п/с колеб-е звено. Ω1,2 – возм-но возн-е мех-го резонанса.
Рассм. Подробнее дв-е 1й массы (ЭД и все до упр-й сист). Обозн
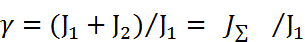 – соотн-е масс.
– соотн-е масс.
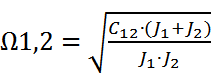 - резон-я частота.
- резон-я частота.
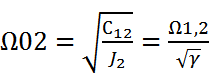 – резон-я частота 2-й массы. (собств-е колеб-я 2-й массы при жесткой заделке 1-й
– резон-я частота 2-й массы. (собств-е колеб-я 2-й массы при жесткой заделке 1-й 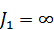 ). Тогда:
). Тогда:
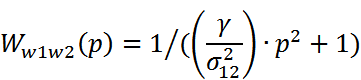
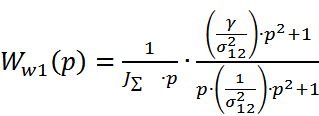 Тогда мех-ю часть ЭП м. представить в виде 3-х звеньев:
Тогда мех-ю часть ЭП м. представить в виде 3-х звеньев:
Тогда
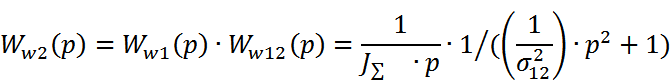
4.. МЕХ-Е ПЕРЕХОДНЫЕ ПРОЦЕССЫ ПРИ ЛИН-Х ЗАВ-СТЯХ M ( w ) ДВИГАТЕЛЯ И MC ( w )
 Измен-е упр-щего или возм-щего возд-я выз-ют в динамич-кой системе ПП-сы. Возможны два случая:1)Мс(w) и М(w) паралл.2) Мс(w) и М(w) не паралл.
Измен-е упр-щего или возм-щего возд-я выз-ют в динамич-кой системе ПП-сы. Возможны два случая:1)Мс(w) и М(w) паралл.2) Мс(w) и М(w) не паралл.
1) 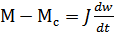
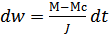
--- 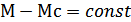 то
то 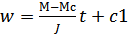 при t=0 c1=wнач
при t=0 c1=wнач
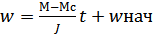 , если М>Мс имеем ускорение иначе замедление
, если М>Мс имеем ускорение иначе замедление
--- 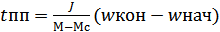
--- 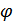 найдём из
найдём из 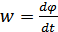
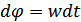
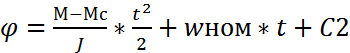 при t =0 C 2=
при t =0 C 2= 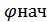 то
то
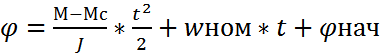 -парабола.
-парабола.
 2)В этом случае м-нт вращения становится не равен моменту сопротивления, возникает динам-й момент:
2)В этом случае м-нт вращения становится не равен моменту сопротивления, возникает динам-й момент:
Из постановки вытекает, что 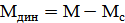 также линейно зав-т от скорости w. Опишем х-ки ур-ми. Введем понятие жесткости мех-й х-ки:
также линейно зав-т от скорости w. Опишем х-ки ур-ми. Введем понятие жесткости мех-й х-ки: 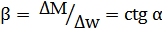
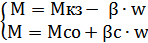 (1)
(1)
M – Mc = J 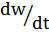 (2) – ур-ние движения.
(2) – ур-ние движения.
J 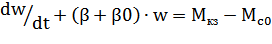
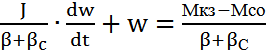
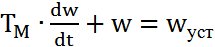
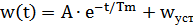
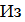 начальных условий при t = 0 А =
начальных условий при t = 0 А = 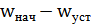
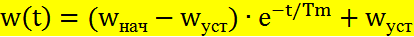 (3)
(3)
Закон изменения момента двигателя во времени: 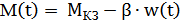
Учитывая значение жесткости. 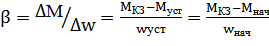
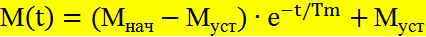
Время пп-са – вр., за кот-е изм-ся w от wнач до wкон или М от Мнач до Мкон, опр-ся из (3) – w или (4) – М путем логарифм-я. 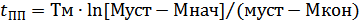
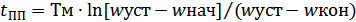 (5)
(5) 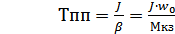
Для случая, когда 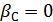 (х-ка параллельна оси скоростей) пар-ры упрощаются и принимают вид:
(х-ка параллельна оси скоростей) пар-ры упрощаются и принимают вид:
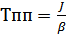
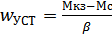
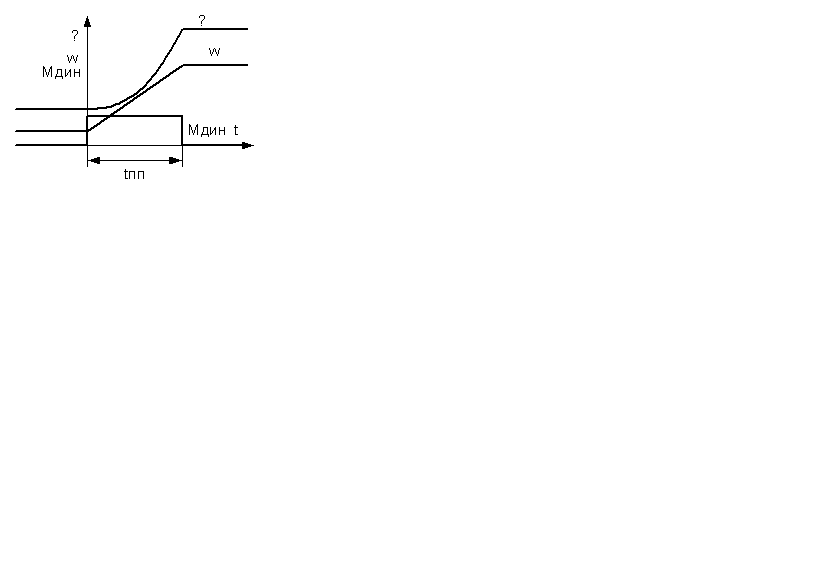
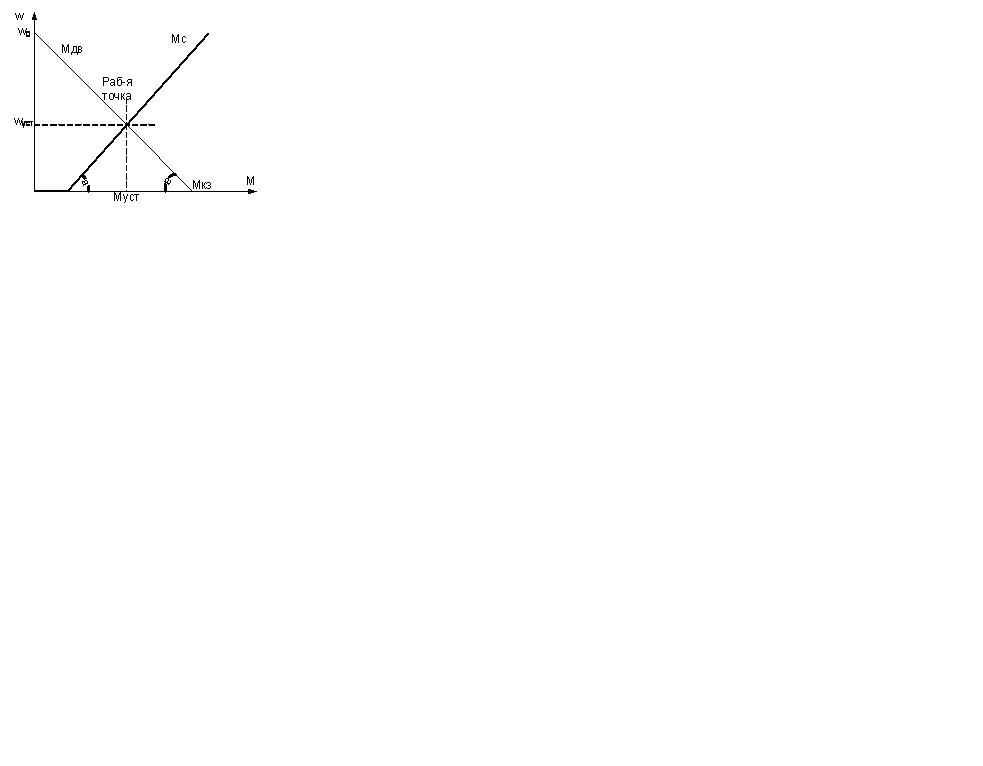
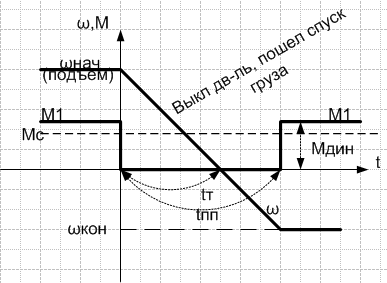
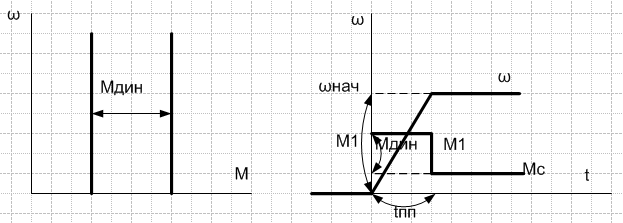
5.. ГРАФ-Й АНАЛИЗ МЕХ-Х ПП-СОВ ПРИ ПУСКЕ И РЕВЕРСЕ С АКТ-НОЙ И РЕАКТ-НОЙ НАГРУЗКАМИ.
Пуск: ωнач=0 при t=0, Мдвиг скачком ↑-ся до М=М1. В этом случае ЭП переходит в режим равномерно ускоренного дв-я с ускорением ε=(М1-Мс1)/J∑
Достигнув требуемой ск-ти, момент двигателя переводится до значения М1=Мс1. Ускорение скачком ↓-ся до нуля, наступает статический режим при
ω= ωном.
Tпуска= 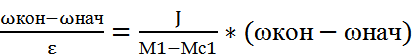
 Т.о., ПП изм-я ск-ти обеспечивается изм-ем мом-та двигателя.
Т.о., ПП изм-я ск-ти обеспечивается изм-ем мом-та двигателя.
ПП с активной нагрузкой Мс (акт-я нагрузка – м. явл-ся ист-ком движ-я). Был подъем груза – необх. сделать спуск. При t=0 уст-вим МЭД=М1=0 (Uя=0) привод замедляется с ускорением
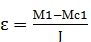 =
= 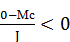 , а ск-ть ω изм-ся по з-ну:
, а ск-ть ω изм-ся по з-ну:
ω= ωнач-(Мс/J∑)t, ч/з время tт= J∑ ωнач/Мс, под дей-м актив-го Мс (груз) ЭД-ль нач-ет ускоряться в противопол-м направлении с возрастающей ск-ю. Когда ω достигнет нужного знач-я tпп, М1=Мдв скачком увеличивают до М1=Мс и наступает статический режим ωкон=const.
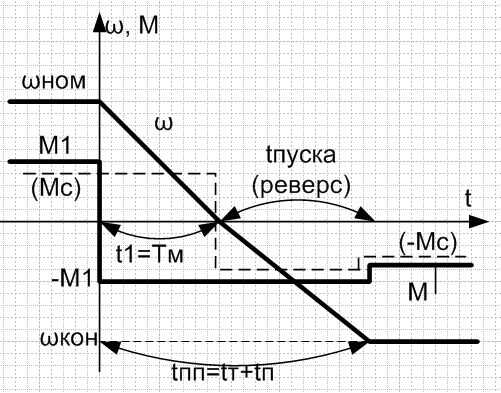 Реверс при реактивной нагрузке – меняется знак Мс при изм-ии знака ω. Пусть при t=0, момент ЭД-ля скачком изм-ся до (–М1), тогда ω изм-ся (ЭП тормозится).
Реверс при реактивной нагрузке – меняется знак Мс при изм-ии знака ω. Пусть при t=0, момент ЭД-ля скачком изм-ся до (–М1), тогда ω изм-ся (ЭП тормозится).
ω=ωНАЧ-(М1+Мс/J∑)t=ωнач-εЕ.; tт=J∑(-ωнач)/(-М1-Мс)=ωнач/εт(торможение).
При t>t1, ω ЭД-ля под действием Мдвиг; М=-М1, реактив. нагрузки на –Мс1. Мдин резко уменьшается.εт=-М1-Мс/J∑; εп= - М-Мс/J∑; εт> εп. ω=- М1-Мс/J∑*t – линейный з-н изменения ск-ти. Закон изменения скорости в ПП опред-ся хар-м изменения во времени момента двигателя.
6. ДПТ С НВ. СХЕМА, ПРИНЦИП РАБОТЫ, СТАТИЧ-Е ХАР-КИ, ОГРАНИЧЕНИЯ,ПРИМЕНЕНИЕ
ДПТ используется в ЭП механизмов, требующих по технологическим условиям регулирования скорости в широком диапазоне. При этом ЭД-ли со смешанным и последовательным возбуждением, как правило, применяются в разомкнутых системах тягового ЭПа. ЭД-ли с независимым возбуждением в настоящее время являются основой замкнутых систем регулируемого ЭПа.
ДПТ НВ имеет обмотку якоря и обмотку возбуждения, которые в общем случае получают питание от независимых источников постоянного тока. Для процесса электромеханического преобразования энергии необходимо протекание переменных токов хотя бы по части обмоток машины. Выполнение этого условия в машине постоянного тока обеспечивается работой коллектора, коммутирующего пост-й ток, поступающий в якорную обмотку со стороны ист-ка питания, с частотой w эл, равной эл-ской скорости ротора.
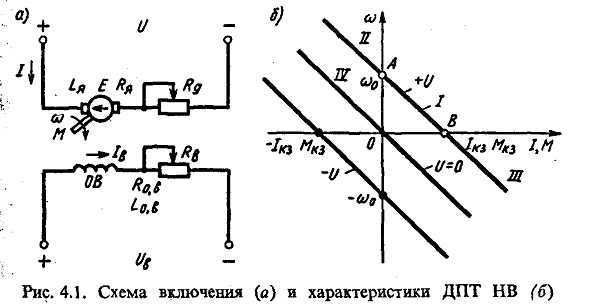
Основная схема включения ДПТ НВ представлена на рис. 4.1 а, где приняты следующие обозначения :
I—токи в цепях обмоток якоря и возбуждения ОВ (А); E-ЭДС якоря (В); w и М—узловая скорость (рад/с) и момент (Н • м) двигателя; Rя = rоя + rдп + rко + rщ — сопротивление якоря, состоящее из сопротивлений обмотки якоря rоя, добавочных полюсов rдп, компенсационной обмотки rко и щеточного контакта rщ; Rов— сопротивление обмотки возбуждения; Lя и Lов — индуктивности обмоток якоря и возбуждения. На схеме показаны добавочные резисторы в цепях обмоток якоря Rд и возбуждения RB, а также отдельные источники питания обмоток якоря и возбуждения с напряжениями соответственно U и Uв
Вывод уравнений для статических характеристик двигателя проведем при следующих допущениях: реакция якоря не учитывается; момент на валу двигателя равен электромагнитному моменту. Уравнение напряжений, выражения ЭДС якоря и электромагнитного момента записываются в таком виде:
 ,
,
где R= Яя + Яд — полное сопротивление цепи якоря Ом; Ф — магнитный поток, Вб; U—подводимое к якорю напряжение, В; k=pN/(2πa) — конструктивный коэффициент двигателя; р — число пар полюсов; N — число активных проводников обмотки якоря; а — число параллельных ветвей обмотки якоря.
Подставляя (4.2) в (4.1), получаем формулу для электромеханической характеристики w(I):

Формула для механической характеристики w (М) ДПТ НВ получается из (4.4) с использованием выражения (4.3):
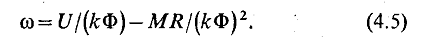
В соответствии с (4.4) и (4.5) электромеханическая и механическая характеристика ДПТ НВ представляют собой линейные зависимости угловой скорости (в дальнейшем скорости) от тока и момента, вид которых для разных полярностей питающего якорь напряжения показан на рис. 4.1,6. На рисунке электромеханическая и механическая характеристики совмещены, что в соответствии с (4.3) справедливо в случае кФ = const. Их характерными точками являются точка А холостого хода, в которой w = w0, а I=М=0, и точка В короткого замыкания, где w = 0, а I=Iкз и М=Мкз. Отметим, что режим короткого замыкания для электрической машины соответствует неподвижному состоянию якоря при поданном на двигатель напряжении, а не замыканию его электрических цепей между собой или на корпус. Режим короткого замыкания называется также пусковым режимом, поскольку является начальным при включении (пуске) двигателя.
Уравнения (4.4) и (4.5) можно представить в сокращенной форме записи:

где w0—скорость идеального холостого хода двигателя,

Δw — изменение скорости относительно скорости идеального холостого хода,
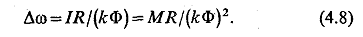
На рис. 4.1,б показана также характеристика ДПТ НВ при U=0, уравнение которой получаются из (4.4) и (4.5):
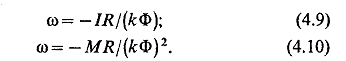
7. ДИНАМИЧ-Я МОДЕЛЬ ДПТ НВ И ЕГО СТРУКТУРНАЯ СХЕМА
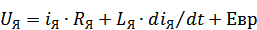 - ур-е эл-го равн-я, эл-я цепь якоря.
- ур-е эл-го равн-я, эл-я цепь якоря.
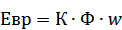 - ЭДС вращения якоря – влияние реальной нагрузки на эл-ю цепь.
- ЭДС вращения якоря – влияние реальной нагрузки на эл-ю цепь.
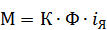 - ур-ние электромех-й связи
- ур-ние электромех-й связи
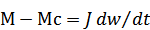 – ур-ние дв-я св. ЭД с мех-мом. СИСТ (1)
– ур-ние дв-я св. ЭД с мех-мом. СИСТ (1)
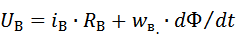 - эл-я цепь возбужд-я
- эл-я цепь возбужд-я
Ф=f( 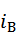 )
)
Где 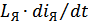 – ЭДС самоиндукции, возник-щая в ПП при измен-и тока якоря,
– ЭДС самоиндукции, возник-щая в ПП при измен-и тока якоря,
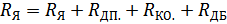 - актив-е R-е якорной цепи (сама обмотка, доп-е полюса, комп-я обмотка, добавочное (реост-е).
- актив-е R-е якорной цепи (сама обмотка, доп-е полюса, комп-я обмотка, добавочное (реост-е).
Полная индуктивность якорной цепи:
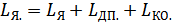
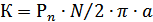 – констр-й коэф-т ЭД, где
– констр-й коэф-т ЭД, где 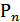 - число пар полюсов, N – число акт-х проводников якоря, участв-х в созд-и м-нта, а – число параллельных ветвей обмотки якоря, Ф – магн-й поток возб-я,
- число пар полюсов, N – число акт-х проводников якоря, участв-х в созд-и м-нта, а – число параллельных ветвей обмотки якоря, Ф – магн-й поток возб-я, 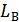 - индук-сть ОВ; М – ЭМ-ный м-нт ЭД, Мс – м-нт сопр-я нагрузки, J – м-нт инерции привода.
- индук-сть ОВ; М – ЭМ-ный м-нт ЭД, Мс – м-нт сопр-я нагрузки, J – м-нт инерции привода.
Преобр-м СИСТ(1) d/dt=р получим:
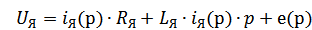
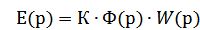
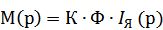
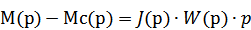 СИСТ (2)
СИСТ (2)
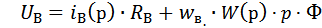
Найдем 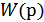 . Для краткости будем опускать зависимость от
. Для краткости будем опускать зависимость от 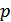
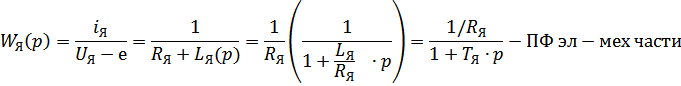
где 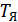 -электромагнитная постоянная времени, для ДПТ=0,02-0,1 с
-электромагнитная постоянная времени, для ДПТ=0,02-0,1 с
ПФ механической части:
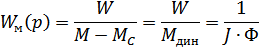
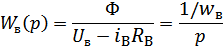
Структурная схема содержит взаимосвязанные контуры:
-якорный
-полюсной
Кривую намагничивания Ф=f( 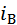 ) представим в виде нелинейного блока(произв.)
) представим в виде нелинейного блока(произв.)








