Лабораторная работа № 1. Активационная функция
МИНИСТЕРСТВО ОБРАЗОВАНИЯ и НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
КАБАРДИНО-БАЛКАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
им. Х.М.Бербекова
Моделирование нейронных сетей
Лабораторный практикум по дисциплинам «Нейрокомпьютерные системы», «Системы искусственного интеллекта» для направлений …
Нальчик, 2012
УДК 681.3
С34 (ББК 32.973.2-018 Я73)
Рецензент:
зав. отделом мультиагентных систем института информатики и проблем регионального управления КБНЦ РАН к.т.н. З. В. Нагоев
Составитель: Бозиев О.Л.
Моделирование нейронных сетей. Лабораторный практикум. – Нальчик: Кабардино-Балкарский Государственный Университет, 2012, 48 с.
Лабораторный практикум предназначен для приобретения навыков моделирования различных типов нейронных сетей для последующего их анализа и обучения решению конкретных задач. Для выполнения лабораторных работ используются средства пакета Neural Network Toolbox системы научных и инженерных расчетов MATLAB.
УДК 681.3
С34
(ББК 32.973.2-018 Я73)
Ó Кабардино-Балкарский Государственный Университет
им. Х.М.Бербекова
Содержание
Лабораторная работа № 1. Активационная функция. 4
Лабораторная работа № 2. Искусственные нейронные сети. 6
Лабораторная работа № 3. Обучение искусственных нейронных сетей. 12
Лабораторная работа № 4. Персептронные сети. 25
Лабораторная работа № 5. Линейные нейронные сети. 28
Лабораторная работа № 6. Сети Эльмана. 34
Лабораторная работа № 7. Сети Хопфилда. 37
Лабораторная работа № 8. Радиальные базисные сети общего вида. 38
Лабораторная работа № 9. Радиальные базисные сети типа GRNN.. 41
Лабораторная работа № 10. Радиальные базисные сети типа PNN.. 42
Лабораторная работа № 11. Самоорганизующиеся слои Кохонена. 44
Лабораторная работа № 12 Самоорганизующиеся карты Кохонена. 46
Литература. 51
Лабораторная работа № 1. Активационная функция
Цель работы: исследование активационных функций и моделей нейронов.
Задание 1. Для активационной функции “жесткая ступенька” hardlim и её производной dhardlim, определяемыми соотношениями
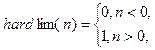
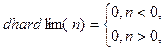
выполнить следующие действия:
1. Вывести на экран информацию об этих функциях с помощью команд:
name=hardlim(′name′) % название функции
dname=hardlim(′deriv′) % название производной
inrange=hardlim(′active′) % диапазон входа
outrange=hardlim(′output′) % диапазон выхода
2. Построить графики функций:
n= –5:0.1:5;
a=hardlim(n);
da=dhardlim(n);
plot(n,a,′r′) % график функции – красный
hold on
plot (n,da,′c′) % график производной – голубой
3. Рассчитать векторы выхода А и производной dA_dN для слоя из трёх нейронов с вектором входа N, состоящим из трёх компонент:
N=[–0,7; 0,1; 0,8];
A=hardlim(N) % вектор выхода активационной функции
dA_dN=dhardlim(N,A) % вектор выхода производной
4. Рассмотренную последовательность команд оформить в виде скрипта и записать в М-файл с именем hardlimfile.
Задание 2. Для симметричной активационной функции “жесткая ступенька” hardlims и её производной dhardlims, определяемыми соотношениями
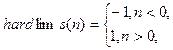
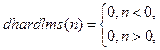
вывести на экран информацию об этих функциях, построить их графики и рассчитать векторы выхода, воспользовавшись скриптом из М-файла hardlimfile. Новый скрипт записать в файл под именем hardlimsfile.
Задания 2-10 (табл. 1). Вывести на экран информацию об указанных функциях и их производных, построить их графики и рассчитать векторы выхода, аналогично заданию 1. Воспользоваться скриптом из М-файла hardlimfile. Новый скрипт записать в файл с указанным именем.
Табл. 1.
| № | Название функции | Функция | Производная | Имя файла |
| 2 | Жесткая ступенька | 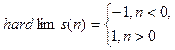
| 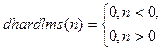
| hardlimsfile |
| 3 | Линейная | рurelin = n | dpurelin = 1 | purelinfile |
| 4 | Положитель-ная линейная | 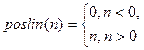
| 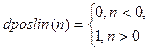
| poslinfile |
| 5 | Линейная с ограничени-ями | 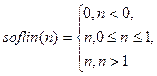
| 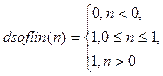
| satlinfile |
| 6 | Симметричная линейная | 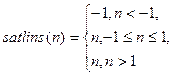
| 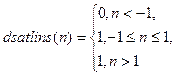
| satlinsfile |
| 7 | Радиальная базисная | radbas = exp(–2n) | dradbas = –2ne(–2n) | radbasfile |
| 8 | Треугольная | 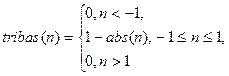
| 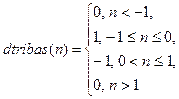
| tribasfile |
| 9 | Логистичес-кая | logsig(n) = = 1/(1 + exp(–n)) | dlogsig(n) = =exp(–n)/(1+exp(–n)2) | logsigfile |
| 10 | Гиперболический тангенс | tansig(n) = = 2/(1 + exp(–2n)) – 1 | dtansig(n) = = 1 – tansig2(n) | tansigfile |
Задание 11. Для конкурирующей функции активации compet, используемой для формирования вероятных и самоорганизующихся нейронных сетей выполнить следующие действия:
1. Вывести на экран информацию об этой функции с помощью следующего скрипта:
Name = compet(′name′) % название функции
Dname = compet(′dеriv′) % название производной
Inrange = compet(′active′) % диапазон входа
Outrange = compet(′outrut′) % диапазон выхода
2. Построить диаграммы для вектора входа и для вектора выхода, используя слой из четырех нейронов:
N = [0; 1; –0.5; 0.5];
A = compet(n);
subplot(2, 1, 1), % подокна 2´1; вывод в 1–е
bar(n), % столбцовая диаграмма
ylabet(‘n’) % метка оси ординат
subplot(2, 1, 2),bar(a),ylabet(‘a’) % во 2–м подокне
3. Рассмотренную последовательность команд оформить в виде скрипта в М-файл с именем competlile.
Задание 12. Выполнить действия 11-го задания для конкурирующей функции активации с мягким максимумом softmax, записав при этом новый скрипт в М-файл с именем softmaxfile.








