Производная по направлению вектора .
Пусть в области D задана скалярная функция u = u ( x ; y ; z ) и выделена поверхность уровня u ( x ; y ; z )=с, на которой взята точка М(х; y ; z ).
Из точки М проведем вектор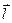 
={ x ; y ; z }, на котором выделим 
.
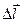Спроектируем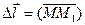 
на плоскость 
xoy : пр xoy Δl =М'М'1. Нормируем вектор ( 
):
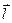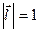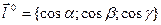, где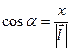 
, 
, 
, 
.
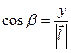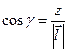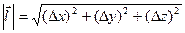Запишем полное приращение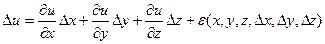 
для u ( x ; y ; z ) , где ε( x , y , z ,Δ x ,Δ y ,Δ z ) – бесконечно малая более высокого порядка.
Разделим приращение Δ u на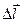 
.
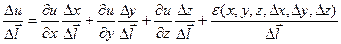Переходя к пределу при 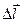→ 0, будем иметь значение производной по направлению вектора 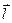в R (3) : 
.
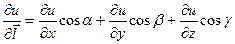Производная по направлению – скорость роста функции u ( x ; y ; z ) по направлению вектора .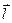
Связь производной по направлению и градиента.
Терема. Если в области D пространства R (3) задана непрерывная дифференцируемая функция u = u ( x ; y ; z ), определены в любой точке D
 |
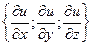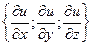градиенты grad u(х;у;z) = , то производная по направлению вектора равна проекции градиента на его направление, то есть 
.
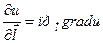Действительно, так как 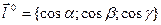, gradu = , то 
.
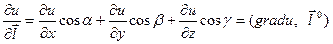С другой стороны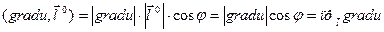 
, где угол между градиентом gradu и вектором 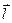обозначен φ.
Следовательно, мы доказали, что .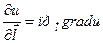
Свойства производной по направлению.
1. Производная по направлению имеет наибольшее значение по направлению градиента, что следует из коллинеарности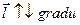 
, то есть cos 0 = 1 и 
.
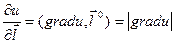2. Производная по направлению равна нулю по направлению, перпендикулярному градиенту, что следует из ортогональности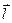 
gradu, то есть cos (π/2) = 0 и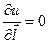 
.
Замечания. 1) Другие обозначения градиента функции:
gradu = gru =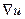 
, где вектор 
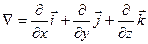называется оператор Гамильтона или оператор набла.
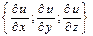Тогда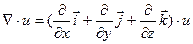 
= 
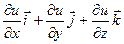= – разные формы записи градиента.
2) 
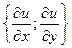Если функция u = u ( x , y ) 
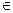R (2), то градиент функции – это вектор 
= 
= ,
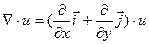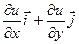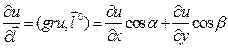а производная по направлению – число, равное .
Пример 3. Найти производную функции u = x 2 + y 2 + z 2 по
направлению вектора 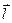= {2;1;-2} в точке М(1;1;1).
Производную функции u = x 2 + y 2 + z 2 по направлению вектора
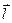={2;1;-2}
найдем по определению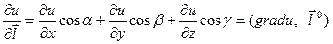 
.
Вычислим градиент gradu = 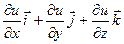= {2 x ; 2 y ; 2 z } в произвольной точке, а затем в точке М(1;1;1): gradu (М) = {2; 2; 2}.
Нормируем вектор 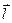= {2;1;-2}.
Для этого найдем его длину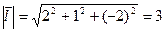 
и координаты единичного вектора 
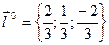, где cosα = 2/3; cosβ = 1/3; cosγ = – 2/3/
.
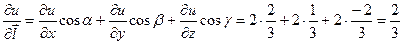