Градиент и производная по направлению.
1) Линии и поверхности уровня.
2) Градиент функции.
3) Производная по направлению.
Если в пространстве R (2) в некоторой области D задана функция двух переменных u = u ( x ; y ), то совокупность точек области D , в которых u ( x ; y )=с, (с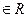 
) образуют линии, называемые линиями уровня.
Если в пространстве R (3) в некоторой области D задана функция трех переменных u = u ( x ; y ; z ), то совокупность точек области D , в которых u ( x ; y ; z )=с, (с 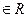) образуют поверхности, называемые поверхностями уровня.
Пример 1. Построить линии или поверхности уровня для функций
1) u ( x ; y ) = x + y ; 2) u ( x ; y ) = - x 2 + y ; 3) u ( x ; y ; z ) = x 2 + y 2 – z.
1) Уравнения линий уровня х + у = с, то есть это семейство прямых, параллельных друг другу, заполняющих всю координатную плоскость хоу, нигде не пересекающихся.
2) Уравнения линий уровня у – х2 = с, то есть это
семейство парабол у = х2 + с, смещенных по оси
оу на const = c, заполняющих всю координатную
плоскость хо y и нигде не пересекающихся.
 |
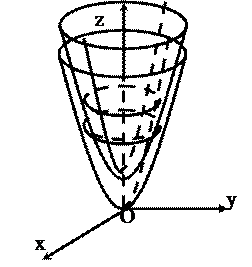3) Уравнения поверхностей уровня
x 2 + y 2 – z = с или x 2 + y 2 = z + с, то есть
семейство параболоидов, смещенных
на const = c (с 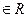) по оси oz , заполняющих
все пространство R (3) и нигде
не пересекающихся. На рисунке
изображены две поверхности
уровня.
Градиентом дифференцируемой функции u = u(x;y) (u = u ( x ; y ; z )) называется вектор, перпендикулярный к линии (поверхности) уровня функций u = u ( x ; y ) ( u = u ( x ; y ; z )):
 |  | ||
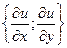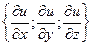grad u(х;у) = в R (2); grad u(х;у;z) = в R (3).
Пример 2. Найти градиент функции u ( x ; y ) = x 2 + y к линии уровня при с = 1 в точках А(0;1) и В(1;0).
 |
Уравнения линий уровня х2 + у = с.
Выделим из семейства линий уровня линию
при с = 1: х2 + у =1. Это парабола
у =1 – х2 с вершиной в точке (0;1) и ветвями,
направленными вниз.
Найдем градиент в произвольной точке:
| |
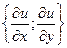grad u(х;у) = = {2x; 1};
в точке А(0;1): grad u(х;у) = {0; 1}; в точке В(1;0): grad u(х;у) = {2; 1} и они перпендикулярны к линии уровня в данных точках.