Не все алгебраические конструкции описываются алгебраическими системами, в качестве примера иных можно упомянуть коалгебры, биалгебры, алгебры Хопфа и комодули над ними.
Список алгебраических систем
§ Множество можно считать вырожденной алгебраической системой с пустым набором операций и отношений ([1] — С.15).
Группоиды, полугруппы, группы
§ Группоид — множество с одной бинарной операцией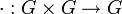 
, обычно называемой умножением.
§ Правая квазигруппа — группоид, в котором возможно правое деление, то есть уравнение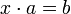 
имеет единственное решение для любых a и b.
§ Квазигруппа — одновременно правая и левая квазигруппы.
§ Лупа — квазигруппа с единичным элементом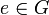 
, таким, что 
.
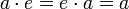§ Полугруппа — группоид, в котором умножение ассоциативно: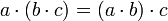 
.
§ Моноид — полугруппа с единичным элементом.
§ Группа — моноид, в котором для каждого элемента a группы можно определить обратный элемент a−1, такой, что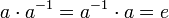 
.
§ Абелева группа — группа, в которой операция коммутативна, то есть,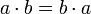 
. Операцию в абелевой группе часто называют сложением ('+').
Кольца
§ Полукольцо — похоже на кольцо, но без обратимости сложения.
§ Почти-кольцо — также обобщение кольца, отличающееся от обычного кольца отсутствием требования коммутативности сложения и отсутствием требования дистрибутивности умножения по сложению (левой или правой)
§ Кольцо — структура с двумя бинарными операциями: абелева группа по сложению, моноид по умножению, выполняется закон дистрибутивности: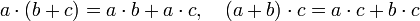 
.
§ Коммутативное кольцо — кольцо с коммутативным умножением.
§ Целостное кольцо — кольцо, в котором произведение двух ненулевых элементов не равно нулю.
§ Тело — кольцо, в котором ненулевые элементы образуют группу по умножению.
§ Поле — коммутативное кольцо, являющееся телом.
Алгебры
§ Алгебра (линейная) — пространство с билинейной дистрибутивной операцией умножения, иначе говоря, кольцо с согласованной структурой пространства
§ Ассоциативная алгебра — алгебра с ассоциативным умножением
§ Алгебра термов
§ Коммутативная алгебра
§ Градуированная алгебра
§ Алгебра Ли — алгебра с антикоммутативным умножением (обычно обозначаемым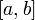 
), удовлетворяющим тождеству Якоби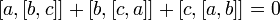 
§ Алгебра Лейбница — алгебра с умножением (обычно обозначаемым 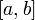), удовлетворяющим тождеству Якоби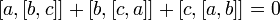
§ Алгебра Йордана — коммутативная алгебра с тождеством слабой ассоциативности: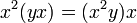 
§ Алгебра некоммутативная йорданова — некоммутативная алгебра с тождеством слабой ассоциативности: 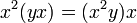и тождеством эластичности: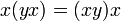 
§ Альтернативная алгебра — алгебра с тождествами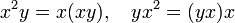 
§ Алгебра Мальцева — антикоммутативная алгебра с тождеством
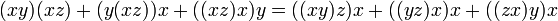
§ Алгебра над операдой — один из наиболее общих видов алгебраических систем. Здесь сама операда играет роль сигнатуры алгебры.
Решётки
§ Решётка — структура с двумя коммутативными, ассоциативными, идемпотентными операциями, удовлетворяющими закону поглощения.
§ Булева алгебра.
3. Содержательное и формальное определение понятия онтологии. Онтологии инженерных знаний. Элементы онтологий. Частные случаи онтологий. Приведите примеры онтологий. Что такое глубина и ширина онтологии? Определите абсолютную, максимальную, среднюю глубину и ширину построенной вами онтологии.