Множество X, на котором введено отношение частичного порядка, называется частично упорядоченным.
Билет №1
1. Что такое системология? Основные понятия системного подхода. Задачи системологии.
Ответ:
Системология (общая теория систем) есть междисциплинарная область, разрабатывающая методологические принципы исследования и моделирования систем любой природы.
Все «жизненные задачи» являются плохо поставленными задачами, из их условия нельзя однозначно извлечь, что является исходными данными, а что результатом, а также – какова связь между ними.
Системология направлена на решение «жизненных задач», на выяснение причин сложностей, возникающих при решении какой-либо проблемы.
Системология позволяет по косвенным признакам прогнозировать те или иные процессы и управлять ими.
Системология или системный анализ – наука об общих принципах организации сложных систем.
Основными понятиями системного подхода являются понятия системы и среды, элемента и связи, функции и структуры, организации и поведения, адаптации и развития.
Задача – предоставление в распоряжение потенциального пользователя методов решения всех типов системных задач
Две основные задачи системологии:
1) задача системного анализа – определение особенностей организации системы, исходя из характеристик взаимодействия системы со средой, в также взаимодействия между элементами системы;
2) задача системного синтеза – определение характеристик взаимодействия, исходя из организации системы.
2. Отношения частичного и полного порядка. Формальные определения частично упорядоченных множеств и цепей. Решётки: определения на основе упорядоченных множеств и универсальных алгебр. Что такое примитивная решётка? Графическое представление решёток с помощью диаграммы Хассе.
Ответ:
Бинарное отношение R на множестве X называется отношением порядка, или отношением частичного порядка, если имеют место
§ Рефлексивность: 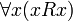
§ Транзитивность: 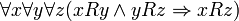 ;
;
§ Антисимметричность: 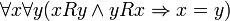 .
.
Множество X, на котором введено отношение частичного порядка, называется частично упорядоченным.
Отношение R, удовлетворяющее условиям рефлексивности, транзитивности, антисимметричности также называют нестрогим, или рефлексивным частичным порядком и обычно обозначают символом 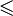 . Если условие рефлексивности заменить на условие антирефлексивности:
. Если условие рефлексивности заменить на условие антирефлексивности:
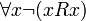 ,
,
то получим определение строгого, или антирефлексивного частичного порядка, обозначаемое обычно символом < . В общем случае, если R — транзитивное, антисимметричное отношение, то
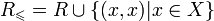 — рефлексивный порядок
— рефлексивный порядок
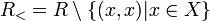 — антирефлексивный порядок.
— антирефлексивный порядок.
Отношение частичного порядка R называется линейным порядком, если выполнено условие
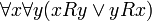
Множество X, на котором введено отношение линейного порядка, называется линейно упорядоченным, или цепью.
Отношение R, удовлетворяющее только условиям рефлексивности и транзитивности, называется квазипорядком, или предпорядком.
Бинарное отношение 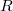 на множестве на множестве 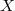 называется отношением линейного порядка, если оно является отношением частичного порядка и обладает следующим свойством: называется отношением линейного порядка, если оно является отношением частичного порядка и обладает следующим свойством: 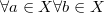 либо либо 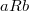 , либо , либо 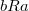 . .
|
Множество 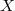 , на котором введено отношение линейного порядка, называется линейно упорядоченным.
, на котором введено отношение линейного порядка, называется линейно упорядоченным.
| Определение: |
Бинарное отношение 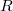 на множестве на множестве 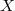 называется отношением полного порядка, если оно является отношением линейного порядка и обладает следующим свойством: называется отношением полного порядка, если оно является отношением линейного порядка и обладает следующим свойством: 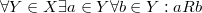 . .
|
Множество 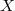 , на котором введено отношение полного порядка, называется полностью упорядоченным.
, на котором введено отношение полного порядка, называется полностью упорядоченным.
Отношение нестрогого порядка обозначают символом 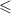 . Запись вида
. Запись вида 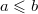 читают как "
читают как "  меньше либо равно
меньше либо равно 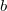 ".
".
Отношение строгого порядка обозначают символом 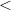 . Запись вида
. Запись вида 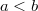 читают как "
читают как "  меньше
меньше 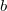 ".
".
Примеры
§ На множестве вещественных чисел отношения «больше» и «меньше» являются отношениями строгого порядка, а «больше или равно» и «меньше или равно» — нестрогого, причем линейного порядка, но не полного.
§ Отношение "являться делителем" на множестве целых чисел является отношением частичного порядка.
§  находится в отношении с
находится в отношении с 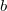 , если
, если 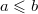 . В качестве множества возьмём натуральные числа. Проверим свойства:
. В качестве множества возьмём натуральные числа. Проверим свойства:
1) 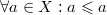
2) 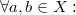 если
если 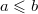 и
и 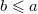 , то
, то 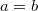
3) 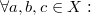 если
если 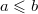 и
и 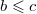 , то
, то 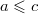
4) 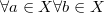 либо
либо 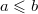 , либо
, либо 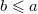 .
.
5) 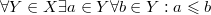 — очевидно, в любом подмножестве натуральных чисел есть наименьшее.
— очевидно, в любом подмножестве натуральных чисел есть наименьшее.
Таким образом данное отношение является отношением полного порядка.

Множество Х на котором вводится отношение линейного порядка называется цепью.

Решётка, структура — частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю (inf) грани. Отсюда вытекает существование этих граней для любых непустых конечных подмножеств.
Примеры
1. множество всех подмножеств данного множества, упорядоченное по включению; например: ; 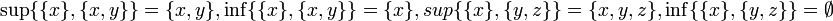
2. всякое линейно упорядоченное множество; причём если 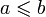 , то sup(a,b) = b,inf(a,b) = a;
, то sup(a,b) = b,inf(a,b) = a;
3. множество всех подпространств векторного пространства, упорядоченных по включению, где inf — пересечение, а sup — сумма соответствующих подпространств;
4. множество всех неотрицательных целых чисел, упорядоченных по делимости: 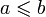 , если b = ac для некоторого c. Здесь sup — наименьшее общее кратное, а inf — наибольший общий делитель данных чисел;
, если b = ac для некоторого c. Здесь sup — наименьшее общее кратное, а inf — наибольший общий делитель данных чисел;
5. вещественные функции, определённые на отрезке [0, 1], упорядоченные условием 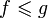 , если
, если 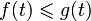 для всех
для всех 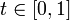 . Здесь
. Здесь
sup(f,g) = u, где u(t) = max(f(t),g(t)).
С помощью отношения доминирования можно ввести другой наглядный способ изображения упорядоченных множеств - диаграммы Хассе. На диаграммах каждый элемент изображается точкой на плоскости, и если y доминирует над x, то точки x и y соединяют отрезком, причем точку, соответствующую x, располагают ниже y.
Рассмотрим три отношения частичного порядка и построим для них диаграммы Хассе.
Пример 2.15. Пусть A = {1, 2, 3}. На множестве всех подмножеств множества A рассмотрим отношение "быть подмножеством". Диаграмма этого упорядоченного множества приведена на рисунке 10(а).
Пример 2.16. Пусть X = {1, 2, 3, 5, 6, 10, 15, 30}. Введем на этом множестве отношение "делится". Диаграмма этого упорядоченного множества приведена на рисунке 10(б).
Пример 2.17. На множестве X = {1, 2, 3, 4, 5, 6, 7, 8} рассмотрим отношение линейного порядка <. Его диаграмма изображена на рисунке 10(в).
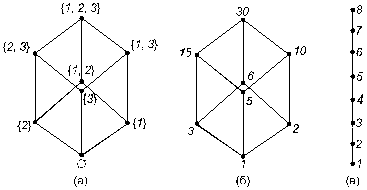
Рис. 10. Диаграммы Хассе
Заметим, что диаграммы Хассе первых двух отношений совпадают. Это означает, что эти частично упорядоченные множества имеют одинаковую структуру, причем отличную от структуры третьего упорядоченного множества, хотя оно тоже содержит восемь элементов. Более точно такая общность структуры определяется понятием изоморфизма.
3. Понятие гранулы. Что такое гранулированная структура информации. Приведите примеры сингулярных и гранулярных значений. Примеры функции распределения случайной величины. Характеристики равномерного, нормального и экспоненциального законов распределения.



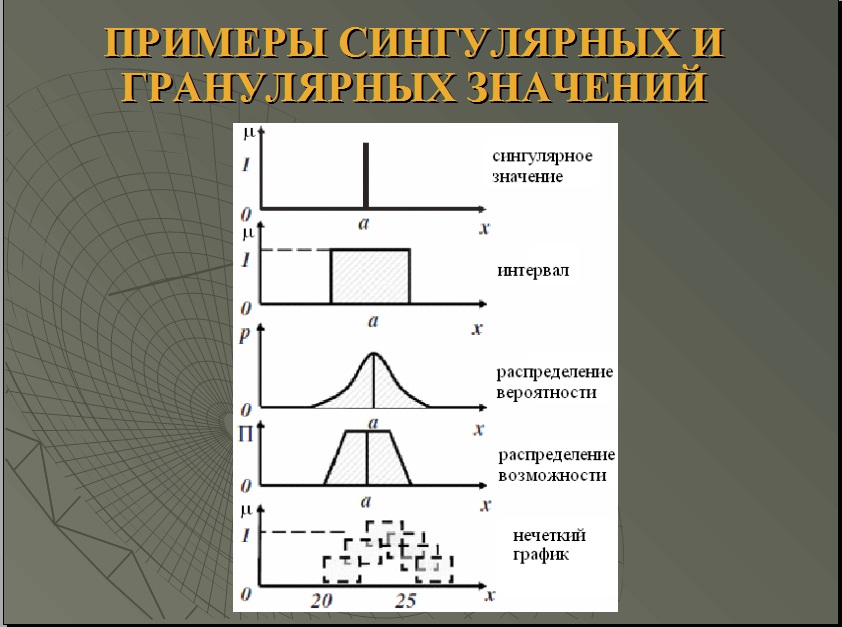
Распределения:
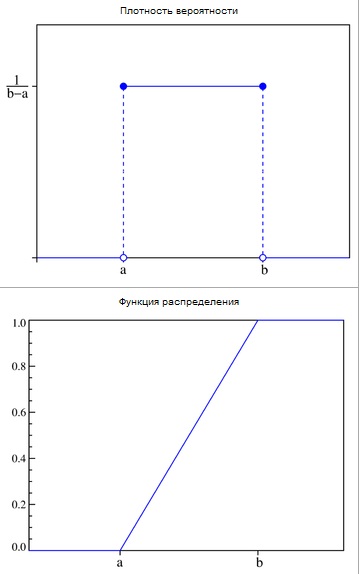
Непреры́вное равноме́рное распределе́ние — в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины.
Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке 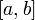 , где
, где 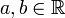 , если её плотность
, если её плотность 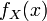 имеет вид:
имеет вид:
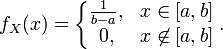
Функция распределения
Интегрируя определённую выше плотность, получаем:
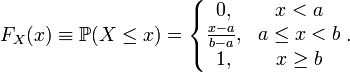
Так как плотность равномерного распределения разрывна в граничных точках отрезка 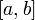 , то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:
, то функция распределения в этих точках не является дифференцируемой. В остальных точках справедливо стандартное равенство:
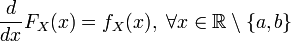 .
.
Билет №2
1. Что такое системный анализ? Как он соотносится с системологией. Что такое треугольник Лемуана? Эволюционирующие системы. Два основных подхода в теории эволюции.
Системный анализ – это методология общей теории систем, заключающаяся в исследовании любых объектов посредством представления их в качестве систем, проведения их структуризации и последующего анализа.
Задачи системного анализа:
- задача декомпозиции – представление систем в виде подсистем, состоящих из более мелких элементов.
- задача анализа – определение закономерностей поведения системы
- задача синтеза – создание модели системы на основе знаний о системе, полученных при решении первых 2-х задач, определяющих структуру, параметры,обеспечивающие решениезадач,эффективное функционирование системы
Системный анализ есть одна из методологий системологии.

Динамическая система – математическая абстракция, предназначенная для описания и изучения эволюционирующих систем.
Требуется дописать.
2. Понятие алгебраической системы: определение и частные случаи.


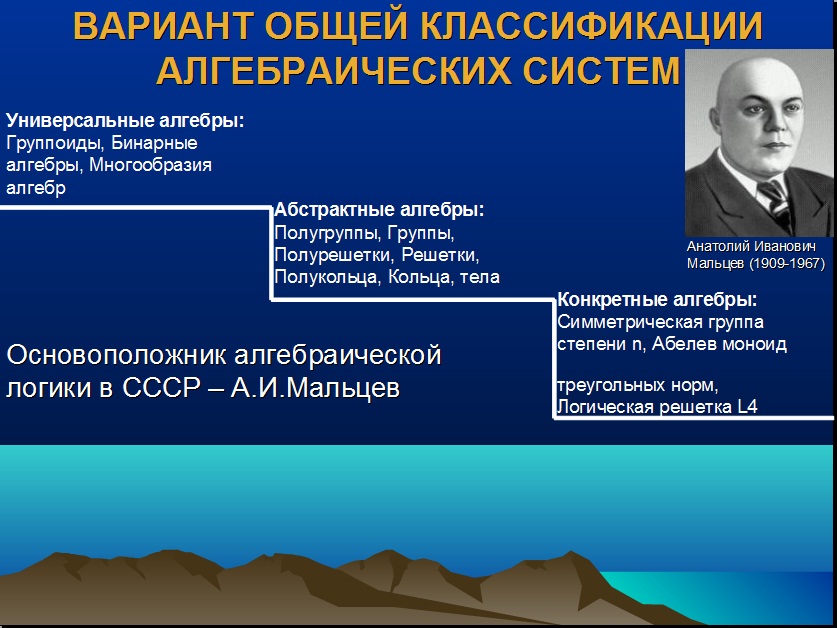
Алгебраическая система или алгебраическая структура — множество G (носитель) с заданным на нём набором операций и отношений (сигнатура), удовлетворяющим некоторой системе аксиом. Понятие алгебраической системы родственно понятию универсальной алгебры.
n-арная операция на G — это отображение прямого произведения n экземпляров множества в само множество 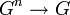 . По определению, 0-арная операция — это просто выделенный элемент множества. Чаще всего рассматриваются унарные и бинарные операции, поскольку с ними легче работать. Но в связи с нуждами топологии, алгебры, комбинаторики постепенно накапливается техника работы с операциями большей арности, здесь в качестве примера можно привести теорию операд (клонов полилинейных операций) и алгебр над ними (мультиоператорных алгебр).
. По определению, 0-арная операция — это просто выделенный элемент множества. Чаще всего рассматриваются унарные и бинарные операции, поскольку с ними легче работать. Но в связи с нуждами топологии, алгебры, комбинаторики постепенно накапливается техника работы с операциями большей арности, здесь в качестве примера можно привести теорию операд (клонов полилинейных операций) и алгебр над ними (мультиоператорных алгебр).
Для алгебраических систем естественным образом определяются морфизмы как отображения, сохраняющие операцию. Таким образом определяются категории групп, колец, R-модулей и т. п.
Если множество обладает структурой топологического пространства, и операции являются непрерывными, то его называют топологической алгебраической системой. Так, в топологической группе операции умножения и взятия обратного элемента являются непрерывными.








