17. Укажите информацию, требующуюся исследователю «на входе» для решения задачи кластеризации.
1. Массив р-мерных наблюдений.
2. Априорные представления о классах.
3. Ожидаемые размеры и число кластеров.
18. Укажите, что является результатом кластеризации (что получается «на выходе»).
На «выходе» мы имеем правило классификации, позволяющее наилучшим в определенном смысле образом разбить имеющиеся р-мерные наблюдения на однородные в определенном смысле группы.
19. Какие виды кластерного анализа вам известны?
Иерархические (делятся на агломерационные и дивизивные) и неиерархические.
20. Как называется графические отражения алгоритма иерархической кластеризации?
1. Дендрограмма
2. Icicle plot (вертикальный и горизонтальный варианты).
21. Сформулируйте свойства, которым должно удовлетворять любое расстояние. Какое из этих свойств выполняется не всегда (например, в психологических исследованиях)?
1) d (O i , O j ) > = 0
2) d (O i , O i ) = 0
3) d ( O i , O j ) = 4*) d ( O i , O j )= d ( O j , O i )
22. Какие виды метрики (расстояний) Вам известны?
1. Расстояние Евклида
2. Расстояние Манхеттена
3. Расстояние Чебышева
4. Квадрат расстояния Евклида
23. Даны 2 четырехмерных наблюдения (2 точки в четырехмерном пространстве). Вычислите между ними расстояния: Евклида, Манхеттен, Чебышёва.
Расстояние Евклида: dist =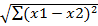 
Расстояние Манхеттен: dist =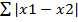 
Расстояние Чебышева: dist = Max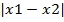 
24. В каком случае применение евклидова расстояния не имеет под собой теоретического основания (хотя может давать разумные результаты)?
25. Назовите известные Вам алгоритмы агломерации.
Алгоритмы агломерации:
- Метод дальнего соседа
- Метод ближнего соседа
- Метод Варда
- Центроидный метод (ищем центр тяжести)
- Метод средней связи (среднее значение всех расстояний между кластерами)
Методы кластеризации подразделяются на иерархические и неиерархические. Иерархические методы подразделяются на агломерационный и дивензивный.
26. Даны 4 трехмерных наблюдения. Реализуйте их кластеризацию на основе метода ближнего соседа (дальнего соседа, средней связи) и расстояния Евклида (Манхеттен, Чебышев). Постройте дендрограмму
27. Дана дендрограмма. Укажите получившиеся кластеры.
Сколько раз вертикальная палка пересечет ветви, столько и будет кластеров.
28. Какие методы приведения к единой шкале Вы знаете? Даны 5 наблюдений. Приведите их к единой шкале измерения, используя линейное преобразование и z -шкалу.
Методы:
- Стандартизация.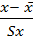 
, где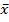 
– среднее значение r wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
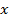, а Sx =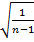 
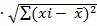
- Линейное преобразование в заданный диапазон значений.
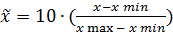, причем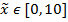 
Если нужно «развернуть» шкалу, то:
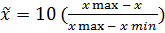, причем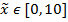
29. Объясните, почему при кластеризации необходимо приводить все показатели к единой шкале измерения?
Показатели, не приведенные к единой шкале, будут оказывать влияние на метрику. Если первый показатель лежит в диапазоне от 1 до 10, а второй – от 200 до 500, то на результаты анализа влияние оказывать будет по большему счету только второй показатель.
30. Укажите недостатки линейного преобразования как процедуры приведения показателей к единой шкале. Нарисуйте картинку, иллюстрирующую ситуацию, когда применение линейного преобразования окажется неудачным выбором.
31. Почему не очень осмысленно применять алгоритмы кластерного анализа для классификации объектов в одномерном или двумерном пространстве?
Потому что там проще построить диаграмму рассеивания и посмотреть самим, какие получатся кластеры.