Свойства кривых безразличия

Дата: 2025-05-01; Просмотры: 7

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

1. Через любую точку в графическом пространстве товаров может быть проведена кривая безразличия.

2. Кривые безразличия не пересекаются. Предположим, что две кривые безразличия пересекаются в точке A (рис. 6.2)

Тогда (по определению кривой безразличия) набор A безразличен набору B и набор A безразличен набору C. Следовательно, по аксиоме транзитивности, наборы B и C также должны быть безразличны друг другу. Но это неверно, так как по аксиоме ненасыщаемости набор B предпочтительнее набора C.

Следовательно, две кривые безразличия не могут иметь общую точку, так как один набор товаров не может характеризоваться двумя различными уровнями полезности.

3. На основании первых двух свойств может быть построена карта безразличия. Кривая безразличия может быть проведена через каждую точку в графическом пространстве товаров, на основании чего мы получаем множество кривых безразличия – карту безразличия, содержащую полную информацию о системе предпочтений потребителя (рис. 6.3).

4. Кривые безразличия (для большинства случаев) имеют отрицательный наклон.

5. Кривые безразличия (для большинства случаев) выпуклы к началу координат.

Для доказательства последних двух свойств вводится понятие предельной нормы замещения (замены) двух товаров, являющееся главной характеристикой системы предпочтений потребителя в ординалистском варианте, так же как в кардиналистском варианте таковым считалась предельная полезность.

Предельная норма замены товаром Х товара Y (MRS_XY) – это количество товара Y, от которого потребитель готов (желает) отказаться, с тем чтобы получить в свое распоряжение дополнительную единицу товара Х, оставаясь при этом на той же кривой безразличия, то есть при том же уровне общей полезности.

Алгебраически MRS_XY может быть записана следующим образом:

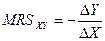. (6.4)

Знак минус перед дробью ставится для того, чтобы оперировать положительными значениями предельной нормы замены.

Геометрически предельная норма замены иллюстрируется тангенсом угла наклона кривой безразличия (рис. 6.4).

Рассматривая предельную норму замены при бесконечно малых изменениях товара Х (при приближении точки B к точке A), мы получаем следующую формулу:

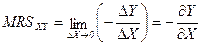. (6.5)