4. Формула коэффициента корреляции Пирсона.
1. Рассмотрите любые 3 показателя социальной, политической или экономической статистики и покажите, что каждый из них следует рассматривать как случайную величину. Приведите примеры не менее 3 случайных факторов, влияющих на каждый из рассматриваемых показателей.
- Измеренный уровень ВВП. Он является случайной величиной, т.к. вычисляется на основе огромного множества факторов, которые мы не в силах полностью описать. Случайные факторы: природные катаклизмы (может быть нарушено производство); наличие теневой экономики (ее невозможно точно измерить); погрешности измерения.
- Показатель уровня брака на каком-либо заводе. Случайные факторы: технические ошибки в работе оборудования; технические ошибки в работе персонала; ошибки, непредвиденные ситуации на производстве.
- Прогноз исхода выборов, полученный в результате проведения exit poll’a. Случайные факторы: отказ граждан отвечать на вопрос; предоставление заведомо ложных ответов интервьюеру; ошибки в сборе информации, допущенные самим интервьюерами.
2. Дайте определение теоретическому коэффициенту корреляции. Что он показывает? В каком диапазоне меняется?
Теоретический коэффициент корреляции – показатель, характеризующий силу взаимосвязи каких-либо двух выбранных показателей. Показывает взаимосвязь, варьируется от 1 до -1 (весь ответ взят из Гугла, не уверен).
3. Почему на практике исследователь не может вычислить сам теоретический коэффициент корреляции?
Теоретический коэффициент корреляции – показатель, характеризующий генеральную совокупность. В своей работе исследователь имеет дело только с выборочным коэффициентом корреляции. Иными словами, исследователь можно измерить коэффициент корреляции для выборки, но не для генеральной совокупности.
4. Формула коэффициента корреляции Пирсона.
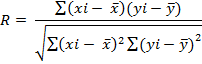
5. Что показывает коэффициент корреляции Пирсона?
Коэффициент корреляции Пирсона показывает функциональную связь между двумя парными показателями.
6. Пусть коэффициент корреляции Пирсона равен 1 – что из этого следует? А если он равен -1?
Если коэффициент корреляции Пирсона равен 1, то исследуемые показатели находятся в прямой линейной зависимости.
Если коэффициент корреляции Пирсона равен -1, то исследуемые показатели находится в обратной линейной зависимости.
7. Пусть коэффициент корреляции Пирсона равен 0,5 – что это значит?
Если коэффициент корреляции Пирсона равен 0,5, то взаимосвязь между объектами может быть описана линейной функцией виде у = 0,5х + b.
8. Назовите не менее двух недостатков коэффициента корреляции Пирсона.
- Коэффициент корреляции Пирсона чувствителен к выбросам
- Коэффициент корреляции Пирсона предназначен для выявления линейной взаимосвязи и может давать искаженные результаты, когда взаимосвязь объектов нелинейна.
9. Формула коэффициента ранговой корреляции Спирмена.
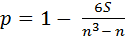, где S = 
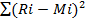. Ri и Mi – ранги наблюдений в первой и второй выборке.
10. Что показывает коэффициент корреляции Спирмена?
Коэффициент корреляции Спирмена показывает степень тесноты связи между ранжировками Х = (х1, х2, х3, …, хn) и У = (у1, у2, у3, …, уn). Он позволяет узнать, существует ли ранговая связь между парными значениями исследуемых переменных. Или, иными словами, он позволяет проверить ранжировки на монотонность.
11. Пусть коэффициент корреляции Спирмена равен 1 – что из этого следует? А если он равен -1?
Если коэффициент корреляции Спирмена равен 1, то между объектами наблюдается положительная монотонная взаимосвязь.
Если коэффициент корреляции Спирмена равен -1, то между объектами наблюдается отрицательная монотонная взаимосвязь.
12. Пусть коэффициент корреляции Спирмена равен 0,5 – что это значит?
Если коэффициент корреляции Спирмена равен 0,5, то между объектами наблюдается некоторая положительная монотонная взаимосвязь.
13. Назовите преимущества и недостатки коэффициента корреляции Спирмена по сравнению с коэффициентом корреляции Пирсона.
Преимущества коэффициента корреляции Спирмена:
- высокая робастность (устойчивость к нетипичным наблюдениям)
- широкая область применения
Недостатки коэффициента корреляции Спирмена:
- не показывает конкретную функциональную связь между двумя переменными
- по большему счету подходит только для фиксации монотонной связи
14. Пусть на основе эмпирических данных вы получили, что R = 0,15 (это коэффициент корреляции Пирсона). Требуется понять, можно ли на основании этого результата утверждать, что на самом деле есть корреляция между иском и игреком. Как это сделать? Дайте ответ, если число наблюдений n = 25.
Решение:
1. H0: Corr (X,Y) = 0 vs. H1: Corr (X,Y)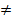 
0
2. 
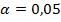
3. 
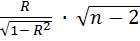
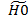t(n-2)
4. Считаем и подставляем в формулу. Потом смотрим по распределению Стьюдента.
15. Пусть на основе эмпирических данных вы получили, что р = 0,15 (где р = коэффициент корреляции Спирмена). Требуется понять, можно ли на основании этого результата утверждать, что на самом деле есть корреляция между иксом и игреком. Как это сделать? n = 25.
Решение:
1. H0: Corr (X,Y) = 0 vs. H1: Corr (X,Y) 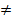0
2. 
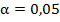
3. 
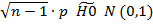
4. Считаем и смотрим ответ. Если он лежит в интервале от -1,96 до 1,96, то H0 верна.
16. Для решения какой задачи применяется кластерный анализ?
Кластерный анализ решает задачу разбиения заданной выборки объектов на подмножества-кластеры таким образом, чтобы каждый кластер состоял из схожих объектов, а объекты из разных кластеров имели между собой как можно более существенные отличия. Главная цель – нахождение групп схожих объектов в выборке.