Методы коррекции систем автоматического управления
Цель работы – изучение методов последовательной и параллельной коррекции САУ, типовых корректирующих устройств и их влияния на динамические свойства и точность систем.
3.1. Основные сведения
Синтез САУ, удовлетворяющей заданным требованиям к точности системы и качеству ее динамики, обычно проводят в два этапа:
1-й этап – проектирование основного регулятора, обеспечивающего заданную точность;
2-й этап – синтез специальных корректирующих устройств (КУ) для стабилизации системы, если она неустойчива, и(или) улучшения ее динамических свойств.
Среди КУ различают последовательные, включаемые в прямой канал системы, и параллельные, представляющие собой, как правило, различного рода обратные связи, чаще местные, т. е. охватывающие часть звеньев прямого канала. Достоинством таких КУ по сравнению с последовательными является то, что при правильном расчете (таком, чтобы в существенном диапазоне частот ЧПФ разомкнутого внутреннего контура была значительно больше единицы) ПФ внутреннего контура определяется в основном ПФ корректирующей обратной связи, вследствие чего вариации параметров звеньев, охваченных обратной связью, слабо влияют на динамику системы. Применяют также КУ, включаемые параллельно звеньям прямого канала.
Синтез САУ в частотной области обычно состоит в формировании желаемой ЛАХ разомкнутой системы с последующим расчетом корректирующего устройства, чаще параллельного, введение которого обеспечит эту ЛАХ. Однако в случае последовательной коррекции часто можно обойтись более простой процедурой введения в систему типовых КУ. Объединяя одним понятием "регулятор в прямом канале" основной регулятор и последовательное КУ, можно указать следующие типовые регуляторы, широко применяемые для улучшения динамики и повышения точности систем:
· П-регулятор: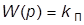 
(при 
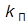> 1 увеличивает 
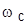и уменьшает 
);
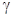· И-регулятор: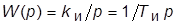 
(повышает порядок астатизма и уменьшает 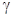на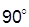 
);
· ПД-регулятор (форсирующее звено):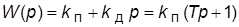 
(повышает 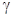; реализуемая ПФ 
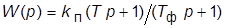, где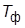 
<< 
);
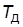· ПИ-регулятор: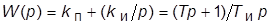 
(обладает свойствами П-регулятора и первым из свойств И-регулятора);
· ПИД-регулятор: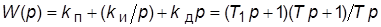 
(сочетает свойства ПИ- и ПД-регуляторов; реально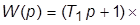 
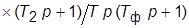, где 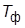– малая постоянная времени).
Некоторые способы определения порядка астатизма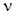 
системы в отношении воздействия 
:
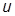· представить ПФ для ошибки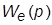 
= E(p)/U(p) в виде 
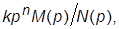где M(p) и N(p) – полиномы, причем 
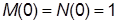; тогда 
;
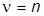· определить порядок астатизма как максимальное число не охваченных местными обратными связями интегрирующих звеньев в обратной связи системы с входом u и выходом e (ошибкой).
3.2. Программа работы
1. Задать структурную схему (рис. 3.1, где y – регулируемая переменная; g и f – задающее и возмущающее воздействия; e – ошибка). Назначить произвольное значение T из диапазона 0.1…1.0 с.
2. Получить ПХ по задающему воздействию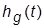 
и определить 
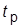и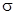 
для ряда возрастающих значений k: 
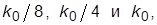где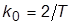 
– номинальное значение k. Описать, как с ростом 
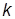изменяются характер переходного процесса и значения показателей качества ПХ.
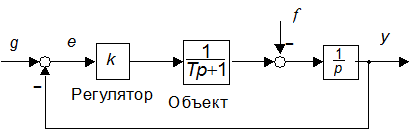
Рис. 3.1
3. Получить ПХ по возмущающему воздействию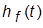 
(g = 0, f = 1) и определить 
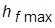и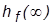 
, задав 
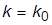. Найти установившуюся ошибку 
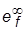на входе регулятора от возмущения f = 1. Убедиться, что 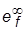½ ½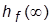=½ 
½.
4. Задать новую ПФ регулятора вида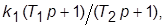 
приняв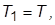 
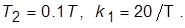Оценить количественно изменение значени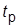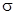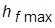й 
, , и 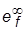. Пояснить результаты для 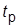и 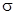, записав ПФ и построив асимптотические ЛАХ разомкнутой системы для обоих регуляторов.
5. Сохранив численные значения параметров схемы, дополнить ее, включив в прямой канал последовательно еще одно КУ с ПФ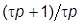 
, задав значение 
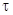не менее (10…20) 
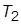. Изменилась ли ПХ по задающему воздействию? Что произошло с ошибкой 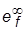? Изменился ли порядок астатизма по возмущению?
6. Задать схему (рис. 3.2) при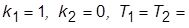 
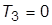(исходная система). Получить ПХ и сделать суждение об устойчивости исходной системы. Стабилизировать систему уменьшением 
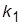. Измерить 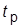и 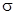. Определить приблизительное критическое значение .
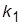7. Восстановить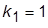 
. Вводя по отдельности корректирующие связи с передачам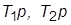и 
и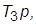 
добиться стабилизации системы. Определить приемлемые с точки зрения качества ПХ значения 
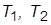и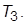 
Для каждой связи сделать эскиз ПХ и измерить 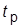и .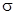
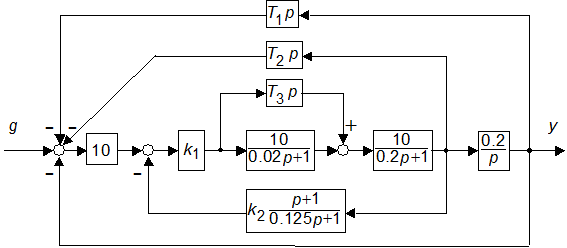
Рис. 3.2
8. Задать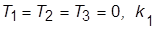 
из диапазона 32…50, 
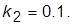Получить ПХ, сделать ее эскиз или копию экрана и зафиксировать 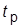и .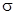
3.3. Содержание отчета
1. Структурные схемы и численные значения их параметров.
2. Результаты по каждому пункту программы работы и комментарии к ним. Ответы на вопросы, содержащиеся в программе.
3. Указание типа использованного регулятора (П-, ПИ- и т. п.).
4. Асимптотические ЛАХ первой системы, согласно пп. 4 и 5 программы.
5. Асимптотические ЛАХ второй системы: исходной и скорректированной введением связей с передачам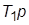и 
и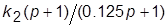 
(все ЛАХ – для разомкнутой системы). В последнем случае использовать правило приближенного построения результирующей ЛАХ соединения с обратной связью.
Контрольные вопросы
1. Как выглядят ЛЧХ ПД-, ПИ-, и ПИД-регуляторов ?
2. Как определить порядок астатизма системы по заданному воздействию?
3. Почему ПД-регулятор повышает запас устойчивости, а ПИ-регулятор – порядок астатизма?
4. Как наклон ЛАХ разомкнутой системы на частоте среза и в ее окрестности влияет на динамические свойства системы?
5. Как называются корректирующие устройства на рис. 3.2?
Лабораторная работа №4