Сибирский государственный аэрокосмический университет
Федеральное агентство по образованию
Сибирский государственный аэрокосмический университет
имени академика М. Ф. Решетнева
А.В. Мурыгин, А.Н. Бочаров
ТЕОРИЯ ИНФОРМАЦИИ
И КОДИРОВАНИЯ
Утверждено редакционно-издательским советом
университета в качестве л абораторного практикума
для студентов специальностей 230102,
очной и заочной формы обучения
Красноярск 2007
УДК 004.07
ББК 32.973.2
С 22
Рецензенты
доктор технических наук, профессор И.В. Коваленко
(Сибирский государственный аэрокосмический университет
имени академика М. Ф. Решетнева)
Мурыгин, А. В.
С 22 Теория информации и кодирования: лаб. практ. / А. В. Мурыгин, А. Н. Бочаров ; Сиб. гос. аэрокосмич. ун.-т. – Красноярск, 2007. – 27 с.
В работе рассмотрены основы теории информации, вопросы информационной метрики, оптимального неравномерного кодирования, принципы построения корректирующих кодов
УДК 004.07
ББК 32.973.2
© Сибирский государственный аэрокосмический
университет имени академика М. Ф. Решетнева, 2007
© А. В. Мурыгин, А. Н. Бочаров, 2007
ОГЛАВЛЕНИЕ
| Предисловие ………………………………………………………………….. | 4 |
| 1. Информационная метрика ......................................................................... | 5 |
| 1.1. Энтропия и ее свойства ………………………………………….... | 5 |
| 1.2. Энтропия сложной системы ………………………………………. | 7 |
| 1.3. Условная энтропия. Объединение зависимых систем …………... | 8 |
| 1.4. Определение информационных потерь в каналах связи ………... | 9 |
| 2. Кодирование информации ……………………………………………….. | 10 |
| 2.1. Количественное определение избыточности в сообщениях…….. | 10 |
| 2.2. Оптимальное неравномерное кодирование ……………………… | 11 |
| 2.2.1. Кодирование методом Шеннона-Фано ………………….. | 11 |
| 2.2.2. Кодирование методом Хаффмана ………………………... | 12 |
| 2.2.3. Определение оптимальности закодированных сообщений | 12 |
| 2.3. Корректирующие коды ……………………………………………. | 13 |
| 2.3.1. Код Хемминга …………………………………………....... | 15 |
| 2.3.2. Линейные групповые коды ………………………………. | 16 |
| 3. Указания к выполнению лабораторных работ ……………………...... | 18 |
| 3.1. Лабораторная работа № 1. Энтропия как мера степени неопределенности системы ……………………………………………………. | 18 |
| 3.2. Лабораторная работа № 2. Энтропия сложной системой. Условная энтропия ……………………………………………………………. | 19 |
| 3.3. Лабораторная работа № 3. Определение избыточности сообщений. Оптимальное неравномерное кодирование ……………………... | 21 |
| 3.4. Лабораторная работа № 4. Определение и исправление ошибок в сообщении. Код Хемминга …………………………………………... | 22 |
| 3.5. Лабораторная работа № 5. Линейные групповые коды………….. | 24 |
| Заключение …………………………………………………………………… | 26 |
| Библиографический список ………………………………………………… | 27 |
ПРЕДИСЛОВИЕ
Теория информации (ТИ) представляет собой направление статистической теории связи, основы которой были заложены классическими трудами Н. Винера, А.Н. Колмогорова, В.А. Котельникова и К. Шеннона.
Круг проблем, составляющих основное содержание теории информации, представляют исследования методов кодирования для экономного представления сообщений различных источников и для надежной передачи сообщений по каналам связи с помехой.
В основе ТИ лежит статистическое описание (статистические модели) источников сообщений и каналов связи, а также измерение количества информации, передаваемое по каналам от источников. При этом количество информации определяется только вероятностными свойствами сообщений.
Предметом ТИ являются теоремы, устанавливающие предельные возможности различных методов обработки и передачи сообщений. Эти предельные возможности зависят только от статистических свойств источников и каналов.
Все задачи, стоящие перед теорией информации, направлены на решение двух основных проблем. Первая основная проблема – проблема эффективности передачи информации. Проблема эта состоит в том, чтобы передать наибольшее количество сообщений наиболее экономным способом.
Вторая основная проблема – проблема надежности передачи информации. Вследствие влияния помех переданная информация искажается. Теория указывает общие пути повышения достоверности передачи информации.
Требования эффективности и надежности в известной степени противоречивы. Теория помогает отысканию приемлемого компромисса.
Всякий раз, решая подобные проблемы, пытаются найти предельные значения количества двоичных символов, скорость передачи или величины ошибок, а также пытаются найти способ обработки сообщений (кодирование и декодирование), который позволяет достичь указанных пределов.
Теория информации является важным инструментом анализа различных технических систем передачи информации, с помощью которого можно определить в какой мере проектируемая система уступает теоретически возможной.
Первоначально ТИ возникла из инженерных задач радиосвязи и телеграфии. Дата рождения ТИ – 1948 г., после появления трудов Клода Шеннона "Математическая теория связи" и "Связь при наличии шума".
Начиная с этого времени ТИ бурно развивалась благодаря работам математиков и инженеров. Основная часть теоретических работ носит математически сложный характер.
В данной работе рассмотрены практические вопросы информационной метрики, оптимального кодирования, построение корректирующих кодов.
1. ИНФОРМАЦИОННАЯ МЕТРИКА
Любое сообщение, с которым мы имеем дело в теории информации, представляет собой совокупность сведений о некоторой физической системе. Очевидно, если бы состояние физической системы было известно заранее, не было бы смысла передавать сообщение. Сообщение приобретает смысл только тогда, когда состояние системы заранее неизвестно случайно.
Если в качестве объекта, о котором передается информация, рассматривается физическая система, которая случайным образом может оказаться в том или ином состоянии, то системе присуща некая степень неопределенности.
Поэтому, сведения, полученные о системе, будут тем ценнее и содержательнее, чем больше неопределенность системы до получения этих сведений. Возникает вопрос: что значит «большая» или «меньшая» степень неопределенности, и чем можно ее измерить?
Сравним между собой системы с различной степенью неопределенности.
В качестве первой системы возьмем монету, которая в результате бросания может оказаться в одном из двух состояний: выпал герб или выпала цифра. В качестве второй – игральную кость, которая имеет шесть возможных состояний: 1, 2, 3, 4, 5, 6.
Очевидно, что неопределенность второй системы больше, так как у нее больше возможных состояний, в каждом из которых она может оказаться с одинаковой вероятностью.
Может показаться, что степень неопределенности определяется числом возможных состояний системы. Однако, в общем случае это не так. Допустим, имеется техническое устройство, которое может находиться в двух состояниях: исправно и отказало. Предположим, что до получения сведений вероятность исправной работы устройства 0,99, а вероятность отказа – 0,01. Такая система обладает только очень малой степенью неопределенности, так как можно предугадать, что работать устройство будет исправно. При бросании монеты тоже имеется два возможных состояния, но степень неопределенности гораздо больше.
Поэтому степень неопределенности физической системы определяется не только числом ее возможных состояний, но и вероятностью состояний.
Для измерения неопределенности состояния системы используют специальную величину – энтропию. При получении сообщения о состоянии системы ее неопределенность уменьшается, поэтому количество информации, содержащееся в сообщении, определяют как изменение энтропии системы.
1.1. ЭНТРОПИЯ И ЕЕ СВОЙСТВА
Рассмотрим некоторую систему Х, которая может принимать конечное множество состояний х1, х2, ... хn. Вероятность возникновения каждого состояния р1, р2, ... рn.
Примером системы Х может быть алфавит, у которого под множеством состояний понимаются символы алфавита
В качестве меры неопределенности этой системы в теории информации применяется специальная характеристика, называемая энтропией.
Энтропией системы может быть определена как сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком.
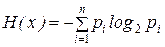 (1)
(1)
Энтропия обладает рядом свойств:
1. Энтропия системы всегда больше нуля.
2. Энтропия обращается в ноль, когда одно из состояний достоверно, а другие невозможны.
3. Энтропия принимает максимальное значение, когда все состояния равновероятны.
4. Энтропия обладает свойством аддитивности, когда несколько систем объединяются в одну, их энтропии складываются.
Рассмотрим простейший случай. Система имеет два состояния и эти состояния равновероятны.
| хi | х1 | х2 |
| рi | 0,5 | 0,5 |
По формуле (1) имеем:
Н(х)=-(0,5log 2 0,5+0,5log 20,5)=1 бит/символ
Логарифм в формуле может быть взят при любом основании а>1. Выбор основания равносилен выбору определенной единицы измерения энтропии. На практике удобнее всего пользоваться логарифмами при основании два и измерять энтропию в двоичных единицах или битах. Таким образом, это энтропия одного двоичного числа, если он с одинаковой вероятностью может быть нулем или единицей.
Для вычисления энтропии вводят специальную функцию:
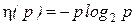 ,
,
Тогда формула энтропии примет следующий вид:
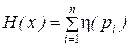
При выполнении преобразований часто более удобной оказывается другая форма записи энтропии, а именно, представление ее в виде математического ожидания
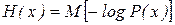 ,
,
где logР(х) – логарифм вероятности любого(случайного) состояния системы, рассматриваемый как случайная величина.
1.2. ЭНТРОПИЯ СЛОЖНОЙ СИСТЕМЫ
Под объединением двух систем X и Y с возможными состояниями x1, x2, …, xn, y1, y2, …, ym понимается сложная система (X, Y), состояние которой (xi,yj) представляют собой все возможные комбинации состояний xi,yj . При этом число возможных состояний системы (X, Y) равно n´m.
В качестве примера сложной системы может быть взят алфавит, имеющий двухбуквенные сочетания.
Обозначим pij вероятность того, что система (X, Y) будет находиться в состоянии (xi,yj). Тогда вероятности pij можно представить в виде таблицы.
| x1 | x2 | … | xn | |
| y1 | p11 | p21 | … | pn1 |
| y2 | p12 | p22 | … | pn2 |
| … | … | … | … | … |
| ym | p1m | p2m | … | pnm |
Энтропия сложной системы равняется сумме произведений вероятностей всех возможных ее состояний на их логарифмы с обратным знаком
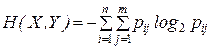 .
.
Энтропию сложной системы, как и энтропию простой, тоже можно записать в форме математического ожидания
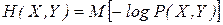 .
.
Если системы X и Y независимы одна от другой, то при объединении систем их энтропии складываются
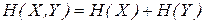 .
.
Это положение называется теоремой сложения энтропий.
1.3. УСЛОВНАЯ ЭНТРОПИЯ. ОБЪЕДИНЕНИЕ ЗАВИСИМЫХ СИСТЕМ
Пусть имеются две зависимые системы X и Y. Обозначим p(yj|xi) условную вероятность того, что система Y примет состояние yj при условии, что система X находится в состоянии xi.
Частная условная энтропия системы Y при условии, что система X находится в состоянии xi определяется следующим образом
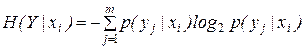 . (2)
. (2)
Для нахождения полной энтропии системы каждая частная энтропия умножается на вероятность соответствующего состояния рi и все произведения складываются
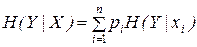 ,
,
где рi – вероятность наступления события хi.
Или
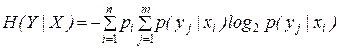 (3)
(3)
После преобразований получаем
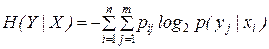 ,
,
где рij=рip(yj|xi).
Выражению также можно придать форму математического ожидания
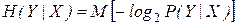 .
.
Таким образом, полная энтропия характеризует степень неопределенности системы Y, остающейся после того, как состояние системы X полностью определилось.
Пользуясь понятием условной энтропии, можно определить энтропию объединенной системы через энтропию ее составных частей В этом случае теорема сложения энтропий для зависимых систем выглядит следующим образом.
Если две системы X и Y объединяются в одну, то энтропия объединенной системы равна энтропии первой ее составной части плюс условная энтропия второй части относительно первой
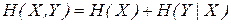 .
.
В частном случае, когда системы X и Y независимы, H ( X | Y ) = H ( Y ), и мы получаем рассмотренную ранее теорему сложения энтропий
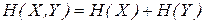 .
.
В другом крайнем частном случае, когда состояние одной из систем полностью определяет собой состояние другой (или, как говорят, системы эквивалентны), получаем:
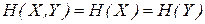 .
.
1.4. ОПРЕДЕЛЕНИЕ ИНФОРМАЦИОННЫХ ПОТЕРЬ В КАНАЛАХ СВЯЗИ
Понятие общей и частной условной энтропии широко используется при вычислении информационных потерь в каналах связи с шумами.
Пусть по каналу связи источником информации передается m сигналов х1, х2, ... хm. На другом конце канала есть приемник, который принимает сигналы y1, y2, ... ym. В канале существуют помехи. При правильном приеме при посылке сигнала x1 принимается сигнал y1 и т.д. Если при посылке сигнала x1 принят yj – это ошибка приема.
Влияние помех в канале связи описывается с помощью канальной матрицы.
| y1 | y2 | ... | yj | ... | ym | |
| x1 | p(y1|x1) | p(y2|x1) | ... | p(yj|x1) | ... | p(ym|x1) |
| x2 | p(y1|x2) | p(y2|x2) | ... | p(yj|x2) | ... | p(ym|x2) |
| ... | ... | ... | ... | ... | ... | ... |
| xi | p(y1|xi) | p(y2|xi) | ... | p(yj|xi) | ... | p(ym|xi) |
| ... | ... | ... | ... | ... | ... | ... |
| xm | p(y1|xm) | p(y2|xm) | ... | p(yj|xm) | ... | p(ym|xm) |
Вероятности, которые расположены по главной диагонали, определяют правильный прием, остальные — ложный. Значения цифр, заполняющих колонки или строки канальной матрицы, обычно уменьшаются по мере удаления от главной диагонали и при полном отсутствии помех все, кроме цифр, расположенных на главной диагонали, равны нулю.
Данная канальная матрица описывает влияние помех со стороны источника сообщений. Прохождение сигнала в канале связи описывается распределением условных вероятностей
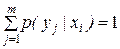
Вероятности, расположенные в одной строке таблицы, составляют полную группу событий.
Потери информации, которые приходятся на сигнал xi можно определить через частную условную энтропию, вычисляемую по формуле (2). Чтобы учесть потери при передаче всех сигналов по каналу связи необходимо вычислить полную условную энтропию по формуле (3)
Если исследуется канал со стороны приемника, то существует вероятность, что при получении сигнала yj был послан какой-то из сигналов x1, x2 ... xm (т. е. yj – известен, xi - неопределен).
При этом канальная матрица имеет вид:
| y1 | y2 | ... | yj | ... | ym | |
| x1 | p(x1|y1) | p(x1|y2) | ... | p(x1|yj) | ... | p(x1|ym) |
| x2 | p(x2|y1) | p(x2|y2) | ... | p(x2|yj) | ... | p(x2|ym) |
| ... | ... | ... | ... | ... | ... | ... |
| xi | p(xi|y1) | p(xi|y2) | ... | p(xi|yj) | ... | p(xi|ym) |
| ... | ... | ... | ... | ... | ... | ... |
| xm | p(xm|y1) | p(xm|y2) | ... | p(xm|yj) | ... | p(xm|ym) |
В этом случае вероятности, расположенные в одном столбце, составляют полную группу событий, и их сумма должна равняться единицы.
Канальная матрица может быть использована для расчета потерь при приеме сигналов yj, как частная энтропия и полная условная энтропия, вычисляемые по формулам:
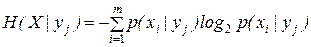
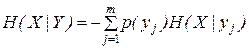
2. КОДИРОВАНИЕ ИНФОРМАЦИИ
2.1. КОЛИЧЕСТВЕННОЕ ОПРЕДЕЛЕНИЕ
ИЗБЫТОЧНОСТИ В СООБЩЕНИЯХ
Если энтропия источника сообщений не равна максимальной энтропии для алфавита с данным количеством качественных признаков (имеются в виду качественные признаки алфавита, при помощи которых составляются сообщения), то это прежде всего означает, что сообщения данного источника могли бы нести большее количество информации. Абсолютная недогруженность на символ сообщений такого источника
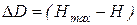
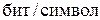 .
.
Для определения количества «лишней» информации, которая заложена в структуре алфавита либо в природе кода, вводится понятие избыточности. Избыточность, с которой мы имеем дело в теории информации, не зависит от содержания сообщения и обычно заранее известна из статистических данных. Информационная избыточность показывает относительную недогруженность на символ алфавита и является безразмерной величиной:
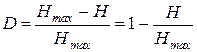 ,
,
где Н и Нmax берутся относительно одного и того же алфавита.
Кроме общего понятия избыточности существуют частные виды избыточности.
1. Избыточность, обусловленная неравновероятным распределением символов в сообщении:
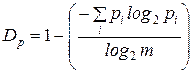 ,
,
где m – количество символов алфавита.
2. Избыточность, вызванная статистической связью между символами сообщения:
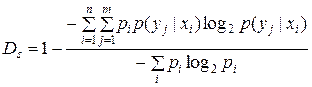 .
.
Полная информационная избыточность определяется следующим образом:
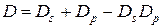 .
.
2.2. ОПТИМАЛЬНОЕ НЕРАВНОМЕРНОЕ КОДИРОВАНИЕ
Избыточность в сообщениях является отрицательным фактором, так как уменьшает пропускную способность канала связи. Уменьшить избыточность можно перераспределив вероятности появления символов алфавита. Для этого символы сообщения кодируют кодами разной длины. Редко встречающиеся символы кодируются длинной кодовой цепочкой, часто встречающиеся – короткой. Такие коды называются оптимальными неравномерными кодами.
2.2.1. КОДИРОВАНИЕ МЕТОДОМ ШЕННОНА-ФАНО
Согласно методике Шеннона-Фано построение оптимального кода ансамбля из сообщений сводится к следующему:
1. Алфавит из n букв (или комбинации букв) располагается в порядке убывания вероятностей их появления в сообшениях.
2. Первоначальный алфавит кодируемых символов (сообщений) разбивается на две группы таким образом, чтобы суммарные вероятности сообщений обеих групп были по возможности равны. Если равной вероятности в подгруппах нельзя достичь, то их делят так, чтобы разница между вероятностями в делимых подгруппах была минимальна.
3. Первой группе присваивается символ 1, второй группе - символ 0.
4. Каждую из образованных подгрупп делят на две части таким образом, чтобы суммарные вероятности вновь образованных подгрупп были по возможности равны.
5. Первым группам каждой из подгрупп вновь присваивается 1, а вторым - 0. Таким образом, получается второй символ кода. Затем каждая из полученных групп вновь делится на равные (с точки зрения суммарной вероятности) части до тех пор, пока в каждой из подгрупп не останется по одной букве.
2.2.2. КОДИРОВАНИЕ МЕТОДОМ ХАФФМАНА
Метод Хаффмана также относится к группе неравномерных кодов. Методика построения кода следующая.
Пусть имеется алфавит А, содержащий буквы а1, а2, ... аn, вероятности появления которых p1, p2, ... pn.
1. Расположим буквы в порядке убывания их вероятностей.
2. Две буквы алфавита А1, объединяем в новую букву (в случае кодирования двоичным алфавитом). Получаем новый алфавит А1.
3. Буквы алфавита А1 также располагаем в порядке убывания их вероятностей.
4. Две последние буквы алфавита А1 объединяются в новую букву. Получаем алфавит А2. Процедура сжатия (образование новых алфавитов) продолжается до тех пор, пока в последнем алфавите не останется две буквы.
Кодирование:
1. Две буквы последнего алфавита кодируются нулем и единицей.
2. Затем кодируется предыдущий алфавит. При этом буквы алфавита имеют те же кодовые комбинации, а к двум последним буквам добавляется ноль или единица.
2.2.3. КОДИРОВАНИЕ МЕТОДОМ ХАФФМАНА.
КОДОВОЕ ДЕРЕВО
На практике зачастую не производят многократного выписывания вероятностей символов с учетом вероятности вновь образованного символа, а обходятся элементарными геометрическими построениями, суть которых сводиться к тому, что символы кодируемого алфавита попарно объединяются в новые символы, начиная с символов, имеющих наименьшую вероятность.
2.2.4. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОСТИ
ЗАКОДИРОВАННЫХ СООБЩЕНИЙ
Оптимальность полученного кода можно определить по следующим параметрам:
1. Средняя длина кода
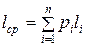 ,
,
где pi – вероятность появления символа первичного алфавита; li – длина кодовой комбинации отдельного символа.
При этом должно выполняться соотношение
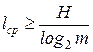 ,
,
где m – число символов вторичного алфавита; Н – энтропия исходного алфавита.
Если используется двоичный алфавит выражение сводится к виду lср≥ H.
3. Коэффициент статистического сжатия
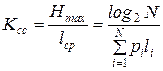 ,
,
где N – число символов первичного алфавита
4. Коэффициент относительной эффективности
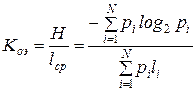 .
.
2.3. КОРРЕКТИРУЮЩИЕ КОДЫ
Корректирующими кодами называются коды, позволяющие обнаруживать и исправлять ошибки, происходящие в процессе передачи из-за влияния помех.
Возможность обнаружения ошибок состоит в том, что для передачи используют не все N0 = 2n возможных кодовых комбинаций, а лишь часть их N < N0.
Используемые комбинации N называются разрешенными, а остальные комбинации N0 – N – запрещенными.
Если в результате передачи первоначальная комбинация превратилась в запрещенную, то это обнаруживает наличие ошибки.
Ошибку можно не только обнаружить, но и исправить. Для этого вводятся понятие минимального кодового расстояния.
Минимальное кодовое расстояние d0 – это минимальное количество символов, на которое все комбинации кода отличаются друг от друга.
Для того чтобы определить кодовое расстояние достаточно просуммировать (по модулю два) кодовые комбинации и подсчитать число единиц в полученной комбинации.
Необходимое для обнаружения и исправления ошибок минимальное кодовое расстояние вычисляется из следующего выражения:
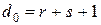
где r – число обнаруживаемых ошибок; s – число исправляемых ошибок.
Для исправления ошибки определяется кодовое расстояние между принятой кодовой комбинацией и разрешенными кодовыми комбинациями. Посланной считается комбинация, имеющая минимальное кодовое расстояние до принятой комбинации.
Для обнаружения и исправления ошибок также необходимо определить соотношение между числом информационных разрядов nи и числом корректирующих разрядов nк, и общей значностью кода n.
В случае обнаружения и исправления одиночной ошибки соотношение между числом информационных разрядов и числом корректирующих разрядов должно удовлетворять следующим условиям:
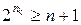 ,
,
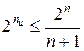 ,
,
при этом подразумевается, что общая длина кодовой комбинации
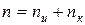 .
.
Для практических расчетов при определении числа контрольных разрядов кодов с минимальным кодовым расстоянием d0 = 3 удобно пользоваться выражениями:
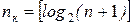 ,
,
если известна длина полной кодовой комбинации n, и
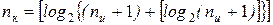 ,
,
если при расчетах удобнее исходить из заданного числа информационных символов nи. Значения логарифмов округляют в большую сторону до целого числа.
На практике информационные и контрольные разряды располагаются по определенной системе. Такие коды называются систематическими. Заложенные при их построении закономерности позволяют обнаруживать и исправлять ошибки с помощью простых приемов. Систематические коды являются равномерными, т. е. все комбинации кода с заданными корректирующими способностями имеют одинаковую длину.
2.3.1. КОД ХЕММИНГА
Код Хемминга является типичным примером систематических кодов. Он позволяет обнаруживать одиночные и двойные ошибки и исправлять одиночные.
Для вычисления основных параметров кода задается либо количество информационных символов, либо количество информационных комбинаций 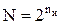 .
.
Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будут рабочими, а какие контрольными. Как показала практика, номера контрольных символов удобно выбирать по закону 2i, где i=0, 2, 4, 8, и т.д. - натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2, 4, 8, 16, 32 и т. д.
Далее составляется вспомогательная таблица для ряда натуральных чисел в двоичном коде (см. таб. 1). Число строк таблицы
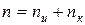 .
.
Первой строке соответствует проверочный коэффициент а1, второй а2 и т.д.
Затем составляются схемы проверок. Проверки производятся суммированием выбранных проверочных коэффициентов. Для каждой проверки выбираются свои проверочные коэффициенты. В первую проверку входят коэффициенты, которые содержат в младшем разряде "1", т.е. а1, а3, а5, а7, а9, а11 и т.д. Во вторую – коэффициенты, содержащие "1" во втором разряде, т.е. а2, а3, а6, а7, а10, а11 и т.д. В третью проверку – коэффициенты, содержащие "1" в третьем разряде, и т.д.
Таблица 1
| n | Двоичный код | Проверочные коэффициенты |
| 1 | 0001 | а1 |
| 2 | 0010 | а2 |
| 3 | 0011 | а3 |
| 4 | 0100 | а4 |
| 5 | 0101 | а5 |
| 6 | 0110 | а6 |
| 7 | 0111 | а7 |
| 8 | 1000 | а8 |
| 9 | 1001 | а9 |
| 10 | 1010 | а10 |
| 11 | 1011 | а11 |
Номер проверки соответствует номеру контрольного разряда в кодовом векторе.
Значения контрольных разрядов определяются следующим образом: сумма единиц проверки должна быть четной. Если эта сумма четна, то значение контрольного разряда – 0 , в противном случае – 1.
При проверке на наличие ошибок в результате передачи кодового сообщения используются правила проверки и строится вектор ошибок S(Sк, ... S2, S1).
В результате первой проверки определяется младший разряд вектора S – S1.
В результате последней проверки определяется старший разряд вектора S– Sк.
Если принятая кодовая комбинация содержит ошибку, то вектор S образует двоичное число, которое указывает номер ошибочной позиции в принятой комбинации.
Для исправления одиночной и обнаружения двойной ошибки, кроме проверок по контрольным позициям, следует проводить еще одну проверку на четность для каждого кода. Чтобы осуществить такую проверку, следует к каждому коду в конце кодовой комбинации добавить контрольный символ таким образом, чтобы сумма единиц в полученной комбинации всегда была четной. Тогда в случае одной ошибки проверки по позициям укажут номер ошибочной позиции, а проверка на четность укажет наличие ошибки. Если проверки позиций укажут на наличие ошибки, а проверка на четность не фиксирует ошибки, значит в коде две ошибки.
2.3.2. ЛИНЕЙНЫЕ ГРУППОВЫЕ КОДЫ
Линейными называются коды, в которых проверочные символы представляют собой линейные комбинации информационных символов.
Для двоичных кодов в качестве линейной операции используют сложение по модулю 2.
Свойство линейных кодов:
1. Сумма (разность) кодовых векторов линейного кода дает вектор, принадлежащий данному коду.
2. Минимальное кодовое расстояние между кодовыми векторами группового кода равно минимальному весу ненулевых кодовых векторов.
Вес кодового вектора (кодовой комбинации) равен числу его ненулевых компонентов.
Расстояние между двумя кодовыми векторами равно весу вектора, полученного в результате сложения исходных векторов по модулю 2.
Групповые коды удобно задавать матрицами, размерность которых определяется параметрами кода nи и nк. Число строк матрицы равно nи, число столбцов равно n.
Такие матрицы называются порождающими, производящими или образующими.
Порождающая матрица 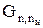 может быть представлена двумя матрицами И и П (информационной и проверочной). Число столбцов матрицы П равно nк, число столбцов матрицы И равно nи:
может быть представлена двумя матрицами И и П (информационной и проверочной). Число столбцов матрицы П равно nк, число столбцов матрицы И равно nи:
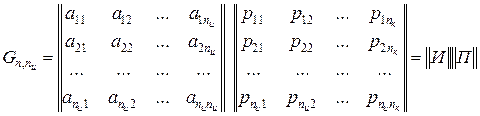 .
.
В качестве матрицы И удобно выбирать единичную матрицу в канонической форме.
При выборе матриц П исходят из следующего соображения: вес каждой строки матрицы П должен быть не менее Wп≥d0-Wи, где Wи – вес соответствующей строки матрицы И. Так как матрица И – единичная, то Wи=1.
Таким образом, порождающая матрица приводиться к виду:
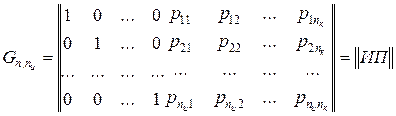 .
.
Строки образующей матрицы G представляют собой nи комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения или исправления ошибки находятся путем суммирования по модулю 2 тех строк матрицы П, номера которых совпадают с номерами разрядов, содержащих единицы в кодовом векторе, представляющем информационную часть кода. Полученную комбинацию приписывают справа к информационной части кода и получают вектор полного корректирующего кода.
В процессе декодирования осуществляются проверки, производящиеся по следующему правилу: в первую проверку в месте с проверочным разрядом р1 суммируются информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы П; во вторую проверку суммируют второй проверочный разряд р2 и информационные разряды, соответствующие единицам второго столбца проверочной матрицы и т.д. Число проверок равно числу проверочных разрядов корректирующего кода nк.
В результате осуществления проверок образуется проверочный вектор S(S1, S2, ... 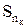 ), который называют синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производиться по виду синдрома.
), который называют синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, то принятая комбинация содержит ошибку. Исправление ошибки производиться по виду синдрома.
Вид синдрома для каждой конкретной ошибки может быть определен при помощи контрольной матрицы Н, которая представляет собой транспонированную матрицу П, дополненную единичной матрицей 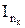 , число столбцов которой равно числу проверочных разрядов кода:
, число столбцов которой равно числу проверочных разрядов кода:
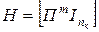 .
.
Столбцы такой матрицы представляют собой значение синдрома для разряда, соответствующего номеру столбца матрицы Н.
3. УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЛАБОРАТОРНЫХ РАБОТ
Порядок выполнения лабораторных работ:
1. Изучить теоретические разделы.
2. Получить вариант задания у преподавателя.
3. Выполнить лабораторную работу.
4. В качестве результата выполнения работы предоставить отчет и программу.
3.1. ЛАБОРАТОРНАЯ РАБОТА № 1
Энтропия как мера степени неопределенности системы
Цель работы: Закрепить теоретические знания и получить практические навыки при вычислении энтропии.
Задание:
1. Получить таблицу значений функции 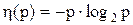 при изменении р от 0.01 до 0.99 с шагом 0.01.
при изменении р от 0.01 до 0.99 с шагом 0.01.
2. Система может находиться в двух состояниях. Вероятность одного состояния Р. Определить значения энтропии при изменении Р от 0,01 до 0,99 с шагом 0,01. Определить максимальное значение энтропии. Построить график.
3. Пользуясь таблицей частот русского языка (таб. 2) определить энтропию одной буквы русского текста.
4. Пользуясь заданным текстовым файлом, определить частоту появления символов в тексте. Определить энтропию одной буквы заданного текста.
Контрольные задачи:
Задание 1
Определить максимальное значение энтропии системы, состоящей из 6 элементов. Каждый элемент может находиться в одном из четырех состояний.
Таблица 2
| Буква | Вероятность | Буква | Вероятность | Буква | Вероятность | Буква | Вероятность |
| Пробел | 0,175 | р | 0,040 | я | 0,018 | х | 0,009 |
| о | 0,090 | в | 0,038 | ы | 0,016 | ж | 0,007 |
| е | 0,072 | л | 0,035 | з | 0,016 | ю | 0,006 |
| а | 0,062 | к | 0,028 | ъ | 0,014 | ш | 0,006 |
| и | 0,062 | м | 0,026 | б | 0,014 | ц | 0,004 |
| н | 0,053 | д | 0,025 | г | 0,013 | щ | 0,003 |
| т | 0,053 | п | 0,023 | ч | 0,012 | э | 0,003 |
| с | 0,045 | у | 0,021 | й | 0,010 | ф | 0,001 |
Задание 2
Алфавит состоит из пяти букв. Определить количество информации на символ сообщения, составленного из этого алфавита, если
а) символы алфавита встречаются с равными вероятностями;
б) символы алфавита встречаются с вероятностями р1 = 0,8; р2 = 0,15; р3 = 0,03; р4 = 0,015; р5 = 0,005.
Задание 3
Определить энтропию источника сообщений, если статистика распределения вероятностей появления символов на выходе источника сообщений представлена следующей таблицей.
| хi | х1 | х2 | х3 | х4 | х5 | х6 | х7 | х8 | х9 | х10 |
| p | 0,35 | 0,035 | 0,07 | 0,15 | 0,07 | 0,07 | 0,14 | 0,035 | 0,01 | 0,07 |
Задание 4
Определить энтропию системы, состоящей из двух элементов. Первый элемент может находиться в двух состояниях с вероятностями р1 = 0,6; р2 = 0,4. Второй элемент может находиться в трех состояниях с вероятностями р1 = 0,1; р2 = 0,4; р3 = 0,5.
3.2. ЛАБОРАТОРНАЯ РАБОТА № 2
Энтропия сложной системы. Условная энтропия
Цель работы: Закрепить теоретические знания и получить практические навыки при определении энтропии.
Задание:
Влияние помех в канале связи описывается канальной матрицей, с помощью условных вероятностей P(Y/X) и P(Х/Y), где X – источник информации, Y – приемник информации.
1. Провести исследование канала информации со стороны источника информации и со стороны приемника информации.
По результатам исследования определить:
- Потери информации Н(Y/xi), которые приходятся на каждый переданный хi сигнал и потери Н(Y/X) при передаче всех сигналов х;
- Потери информации Н(Х/уj), которые приходятся на каждый принятый уj сигнал и потери Н(Х/Y) при приеме всех сигналов yj.
Исходные данные:
Р(уj /xi) и Р(xi / уj) получить из матрицы совместных вероятностей, размером 10 × 10, которую задать самостоятельно.
2. Определить энтропию Н(Х,Y) двухбуквенного сочетания и условную энтропию Н(Y/X) заданного текстового сообщения.
Х – 32-х буквенный алфавит
Y – 32-х буквенный алфавит
Контрольные задачи:
Задание 1
Определить энтропию источника сообщений, если вероятность появления сигналов на входе приемника р(b1) = 0,1; р(b2) = 0,3; р(b3) = 0,4; р(b4) = 0,2, а канальная матрица р(а|b) имеет вид:
| 0,99 | 0,02 | 0 | 0 |
| 0,01 | 0,98 | 0,01 | 0,01 |
| 0 | 0 | 0,98 | 0,02 |
| 0 | 0 | 0,01 | 0.97 |
Задание 2
Определить частную условную энтропию относительно каждого символа источника сообщений при передаче по каналу связи, описанному следующей матрицей совместных вероятностей р(A, B)
| 0,2 | 0 | 0 |
| 0,1 | 0,2 | 0 |
| 0 | 0,1 | 0,4 |
Задание 3
В результате статических испытаний канала связи были получены следующие условные вероятности перехода одного сигнала в другой: p(b1|a1)=0,85; p(b2|a1)=0,1; p(b3|a1)=0,05; p(b1|a2)=0,09; p(b2|a2)=0,91; p(b3|a2)=0; p(b1|a3)=0; p(b2|a3)=0,08; p(b3|a3)=0,92. Построить канальную матрицу и определить общую условную энтропию сообщений, передаваемых по данному каналу связи
Задание 4
Задана матрица вероятностей системы, объединенной в одну систему из двух взаимозависимых систем В и А р(А, В):
| 0,3 | 0 | 0 |
| 0,2 | 0,3 | 0,1 |
| 0 | 0,1 | 0 |
Определить полные условные энтропии Н(B|A) и H(A|B).
3.3. ЛАБОРАТОРНАЯ РАБОТА № 3
Определение избыточности сообщений.
Оптимальное неравномерное кодирование
Цель работы: Закрепление знаний по методам кодирования информации.
Задание:
1. Используя заданный текст определить:
- Избыточность заданного текста, вызванную неравновероятностью появления символов в сообщении;
- Избыточность, вызванную статистической связью между соседними символами;
- Полную избыточность.
2. Используя заданный текст построить оптимальный неравномерный код, применяя:
- Метод Шеннона-Фано;
- Метод Хаффмана.
3. Определить для каждого метода среднюю длину символа исходного алфавита, коэффициент статистического сжатия, коэффициент относительной эффективности
4. Закодировать исходный текст методом Шеннона-Фано и методом Хаффмана.
5. Декодировать текст, закодированный методом Шеннона-Фано и методом Хаффмана.
Контрольные задачи:
Задание 1
Построить код для передачи сообщений методом Шеннона-Фана. Вероятности появления букв первичного алфавита равны: А1 = 0,5; А2 = 0,25; А3 = 0,098; А4 = 0,052; А5 = 0,04; А6 = 0,03; А7 = 0,019; А8 = 0,011. Определить коэффициент статистического сжатия и коэффициент относительной эффективности.
Задание 2
Определить эффективность кода, построенного по методу Шеннона-Фано, составленного из алфавита со следующим распределением вероятностей букв в сообщениях: А = 0,17; Б = 0,13; В = 0,11; Г = 0,09; Д = 0,07; Е = 0,03; Ж = 0,04; И = 0,02; К = 0,31; Л = 0,03.
Задание 3
Чему равна средняя длина кодового слова оптимального кода для первичного алфавита со следующим распределением вероятностей: р(а1) = 0,13; р(а2) = 0,16; р(а3) = 0,02; р(а4) = 0,03; р(а5) = 0,6; р(а6) = 0,01; р(а7) = 0,05?
Задание 4
Построить методом Хаффмена оптимальный код для алфавита со следующим распределением вероятностей появления букв в тексте: A = 0,5; B = 0,15; C = 0,12; D = 0,1; E = 0,04; F = 0,04; G = 0,03; H = 0,02.
Задание 5
Методом Хаффмена(кодовое дерево) построить оптимальный код для алфавита А, Б, В, Г, Д, Е, Ж, З, если вероятности появления букв равны соответственно: 0,06; 0,15; 0,15; 0,07; 0,05; 0,3; 0,18; 0,04.
Задание 6
Построить код Хаффмена для передачи сообщений следующего исходного алфавита: А = 0,24; Б = 0,18; В = 0,38; Г = 0,1; Д = 0,06; Е = 0,02; Ж = 0,02, если число качественных признаков вторичного алфавита равно m2 = 3.
3.4. ЛАБОРАТОРНАЯ РАБОТА № 4
Определение и исправление ошибок в сообщении.
Код Хемминга
Цель работы: Закрепление знаний по методам кодирования информации.
Задание:
Построить код Хемминга для исправления одиночной ошибки и обнаружения двойной ошибки.
Код должен предусматривать возможность посылки n сообщений.
Варианты заданий:
Таблица 3
| Вариант | Кол-во сообщ. n | Вариант | Кол-во сообщ. n | Вариант | Кол-во сообщ. n | Вариант | Кол-во сообщ. n |
| 1 | 16 | 6 | 512 | 11 | 16384 | 16 | 512 |
| 2 | 32 | 7 | 1024 | 12 | 32784 | 17 | 1024 |
| 3 | 64 | 8 | 2048 | 13 | 65536 | 18 | 2048 |
| 4 | 128 | 9 | 4096 | 14 | 128 | 19 | 4096 |
| 5 | 256 | 10 | 8192 | 15 | 128 | 20 | 8192 |
1. Рассчитать параметры кода: nu , nk , n.
2. Привести пример 10 кодовых сообщений
3. Показать процедуру исправления ошибки в одной из позиций (по заданию преподавателя).
4. Составить программу кодирующую и декодирующую кодовую комбинацию.
Контрольные задачи:
Задание 1
Требуется передать 16 сообщений. Построить код Хэмминга, исправляющий одну ошибку.
Задание 2
Построить код Хэминга для информационной комбинации 0101. Показать процесс обнаружения ошибки.
Задание 3
Какой вид имеют комбинации корректирующего кода Хэмминга для передачи сообщений 1101 и 1011? Показать процесс построения корректирующего кода.
Задание 4
Переданы следующие комбинации в коде Хэмминга: 1101001, 0001111, 0111100. Получены – 1001001, 0011111, 0110100. Показать процесс обнаружения ошибки.
Задание 5
Построить код Хэмминга для исправления одиночной ошибки и обнаружения двойной ошибки четырехзначного двоичного кода. Показать процесс построения кода.
Задание 6
Построить код Хэмминга для передачи одиннадцатиразрядной информационной комбинации 10110110110. Показать процесс обнаружения ошибки, которая произошла в пятом разряде соответствующей комбинации корректирующего кода.
Задание 7
Построить код Хэмминга, исправляющий одиночную ошибку. Общее количество сообщений, передаваемых комбинациями полученного кода, должно быть не менее 30.
3.5. ЛАБОРАТОРНАЯ РАБОТА № 5
Линейные групповые коды
Цель работы: Закрепление знаний по методам кодирования информации.
Задание:
1. Построить линейный групповой код, способный исправлять одиночную ошибку. Вариант взять из лабораторной № 4.
2. Привести пример 10 кодовых комбинаций.
3. Показать процесс исправления ошибки в заданном разряде k.
4. Составить программу, кодирующую и декодирующую кодовую комбинацию.
Контрольные задачи:
Задание 1
Источник передает сообщения при помощи 15 двоичных комбинаций. Составить информационную и проверочную матрицы таким образом, чтобы полная производящая матрица могла производить групповой код, корректирующий одиночные сбои.
Задание 2
Групповой код построен по матрице
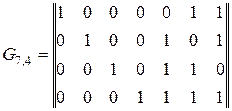 .
.
Показать процесс исправления ошибки в произвольном разряде корректирующего кода, информационная часть которого представляет собой четырехразрядные комбинации натурального двоичного кода.
Задание 3
Определить, какие из приведенных ниже комбинаций групповых кодов содержат ошибку: 1100111, 0110101, 0011010, 0010110, если известно, что код построен по матрице
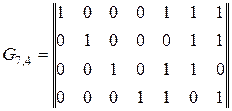
Задание 4
Какой вид имеют комбинации группового кода с d0 = 3, построенного для передачи четырехзначных двоичных комбинаций на все сочетания, если его порождающая матрица имеет вид:
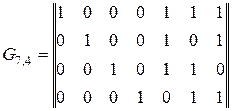
ЗАКЛЮЧЕНИЕ
Необходимо отметить, что современная Теория информации лишь на первый взгляд кажется устоявшейся и уже достигшей завершенности. Несмотря на наличие результатов, носящих законченный характер (теоремы Шеннона, Котельникова), теория в целом находится в состоянии развития. Положение таково, что хорошо изученными могут считаться процессы передачи и хранения информации. Из процессов преобразования информации рассмотрены наиболее простые (перекодировка, линейное предсказание, квантование). Вопросы использования информации остаются пока практически вне рамок теории информации. Одной из причин этого является отсутствие качественных особенностей информации, степени истинности, ценности.
От общей теории часто ожидают больше, чем она может дать, полагают, что теория содержит ответы на любые практические вопросы. Это, конечно, не так. Общая теория устанавливает определенный строй идей и предуказывает пути практической деятельности, но не ее результаты. Иными словами, для того, чтобы теория могла принести пользу, важно, чтобы ею овладели инженеры, непосредственно занятые в области обработки и передачи информации. С этой целью и написано данное пособие.
Библиографический список
1. Венцель, В.С. теория вероятностей [Текст]: Учеб. для вузов / Е.С. Венцель. – М.: Высшая школа, 2002. – 575 с.
2. Задачник по теории информации и кодированию [Текст] / В.П. Цымбал. – Изд. объед. "Вища школа", 1976. – 276 с.
3. Тенников, Ф.Е. Теоретические основы информационной техники / Ф.Е. Тенников. – М.: Энергия, 1971. – 424 с.








