Метод чистой текущей стоимости (ЧТС) состоит в следующем.
1.Определяется текущая стоимость затрат (С), т.е. решается вопрос, сколько инвестиций нужно зарезервировать для проекта.
2. Рассчитывается текущая стоимость будущих денежных поступлений от проекта, для чего доходы за каждый год приводятся к текущей дате. Результаты расчетов показывают, сколько средств нужно было бы вложить сейчас для получения запланированных доходов, если бы ставка доходов была равна ставке процента в банке или дивидендной отдаче капитала. Подытожив текущую стоимость доходов за все годы, получим общую текущую стоимость доходов от проекта (В):
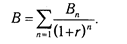
3. Текущая стоимость затрат (С) сравнивается с текущей стоимостью доходов (В). Разность между ними составляет чистую текущую стоимость доходов (ЧТС):
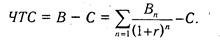
ЧТС показывает чистые доходы или чистые убытки инвестора в результате помещения денег в проект по сравнению с хранением денег в банке. Если ЧТС>0 , значит, проект принесет больший доход, чем стоимость капитала. Если же ЧТС< 0, то проект имеет доходность более низкую, чем стоимость капитала, и поэтому деньги выгоднее оставить в банке. Проект ни прибыльный, ни убыточный, если ЧTC=0.
Если деньги в проект инвестируются не разово, а частями на протяжении нескольких лет, то для расчета ЧТС применяется следующая формула:
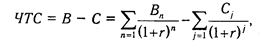
где п - число периодов получения доходов; j - число периодов инвестирования средств.
Предположим, что фирма рассматривает вопрос о том, стоит ли ей вкладывать 360 млн руб. в проект, который может дать прибыль в первый год 200 млн руб., во второй год - 160 и в третий - 120 млн руб. Проценты на капитал составляют 10 %. Иначе говоря, фирме необходима доходность инвестиций минимум 10 %. Стоит ли вкладывать средства в этот проект? Чтобы ответить на поставленный вопрос, рассчитаем ЧТС с помощью дисконтирования денежных поступлений.

Затем рассчитаем текущую стоимость доходов.
Год Денежные поступления Коэффициент Текущая стоимость
млн руб. дисконтирования млн руб.
0 (360) 1,0 (360)
1 200 0,909 181,8
2 160 0,826 132,16
3 120 0,751 __90,12____
404,08
Чистая текущая стоимость денежных поступлений составляет: 404,08 - 360 = 44,08 млн руб.
В нашем примере она больше нуля. Следовательно, доходность проекта выше 10 %. Для получения запланированной прибыли нужно было бы вложить в банк 404 млн руб. Поскольку проект обеспечивает такую доходность при затратах 360 млн руб., то он выгоден, так как позволяет получить доходность большую, чем 10 %.
Второй проект предусматривает капитальные вложения в сумме 500 млн руб. Ожидаемая годовая прибыль - 120 млн руб. на протяжении шести лет. Стоимость капитала равна 15 %. Выгоден ли этот проект? Обеспечит ли он необходимую отдачу капитала?
Текущая стоимость 1 руб. при r = 0,15.
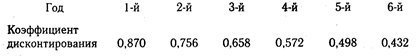
Рассчитаем текущую стоимость всего проекта.

Чистая текущая стоимость денежных поступлений составляет: 454,2 - 500 = -45,8 млн руб. Она меньше нуля, поэтому проект невыгодный.
Если доходы от инвестиций поступают равномерно на протяжении всех лет, можно использовать сокращенную методику расчета. Вместо того чтобы умножать денежные поступления за каждый год на соответствующий ему коэффициент дисконтирования, можно умножить годовой доход на сумму этих коэффициентов. В рассматриваемом примере мы могли умножить 120 млн руб. на сумму коэффициентов (0,870 + 0,658 + 0,572 + + 0,498 + 0,432 =3,785) и получить тот же результат - 454,2 млн руб.
Третий проект предусматривает инвестиции в сумме 400 млн руб. Годовая прибыль ожидается 100 млн руб. Процент на капитал в банке равен 10 %. Выгоден ли этот проект, если его продолжительность: первый вариант - 5 лет; второй вариант - 8 лет.
Текущая стоимость 1 руб. при r = 0,10.

Определим чистую текущую стоимость доходов при разной продолжительности проекта.

Результаты расчетов показывают, что проект невыгоден при продолжительности в пять лет. Начиная с шестого года он обеспечивает более высокий доход, чем капитал, который помещен в банке.
Важной проблемой при прогнозировании эффективности инвестиционных проектов является рост цен в связи с инфляцией. Для того чтобы понять методику учета инфляции, необходимо выяснить разницу между реальной и денежной ставкой дохода.
Предположим, инвестор имеет 1 млн руб., который он желает вложить так, чтобы ежегодно его состояние увеличивалось на 20 %. Иначе говоря, вкладывая 1 млн руб., он надеется через год получить 1,2 млн руб., тогда покупательная способность его денег будет на 20 % выше, чем сейчас, ибо через год он сможет купить на свои деньги на 20 % товара больше, чем в данный момент. Допустим, что темп инфляции 50 % в год. Если инвестор желает получить реальный доход 20 % на свой капитал, то он обязан защитить свои деньги от инфляции. Для этого доход в денежном выражении через год должен быть выше первоначального. Инвестору понадобится дополнительно получить 50 % денег от вложенного капитала для защиты реальной стоимости своего первоначального вклада и 50 % для защиты реального дохода в сумме 0,2 млн руб. Фактический доход, который должен получить инвестор через год в денежном измерении, должен составить 1,8 млн руб. (1,0 млн руб. х 1,5 + + 0,2 млн руб. х 1,5).
Таким образом, денежная ставка дохода, которая нужна инвестору для получения реального дохода в 20 % и защиты от инфляции в 50 %, составит 800 тыс. руб. на 1 млн руб. инвестиций, т.е. 80 %.
Зависимость между реальной и денежной ставкой дохода можно выразить следующим образом:
(1 + г) (1 + т) = 1 + r т, r т = (1 + r) (1 + т) - 1,
где r - необходимая реальная ставка дохода (до поправки на инфляцию); т — темп инфляции, который обычно измеряется индексом розничных цен; rт - необходимая денежная ставка дохода.
В нашем примере денежная ставка дохода определяется так:
1 + rт = 1,2 х 1,5 = 1,8, rт = 1,8 - 1 = 0,8, или 80 %.
Если затраты и цены растут одинаковыми темпами в соответствии с индексом инфляции, то в методах ДДП можно не учитывать инфляцию. Ситуация изменяется, если затраты и цены растут разными темпами. Здесь нельзя производить дисконтирование денежных поступлений, выраженных в постоянных ценах по реальной ставке дохода. Правильный метод - расчет фактических денежных поступлений с учетом роста цен и дисконтирования их по денежной ставке дохода.
Например, компания решает, следует ли ей вкладывать средства в станок, стоимость которого 3,5 млн руб. Он позволяет увеличить объем продаж на 6 млн руб. (в постоянных ценах) на протяжении двух лет. Затраты составят 3 млн руб. Реальная ставка дохода - 10 %, индекс инфляции - 50 % в год. В случае реализации проекта цены на продукцию будут расти всего на 30 %, а затраты - на 60 % в год.
Определим сначала денежную ставку дохода: (1,10 х 1,5) -- 1 = 0,65, или 65 %, а также выручку, затраты и доход.
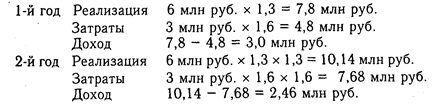
Рассчитаем текущую стоимость доходов.

Чистая текущая стоимость составляет: 2,72 - 3,5 = -0,78 млн руб. Результат отрицательный, следовательно, проект невыгоден для компании.
Если бы мы в этом случае применили реальную ставку дохода 10 % к денежным поступлениям в текущих ценах, то допустили бы ошибку.

Чистая текущая стоимость доходов в этом случае будет больше нуля и составит: 5,2 - 3,5 = +1,7 млн руб. Это неправильный результат.
Таким образом, с помощью метода чистой текущей стоимости (чистого приведенного эффекта) можно довольно реально оценить доходность проектов. Этот метод используется в качестве основного при анализе эффективности инвестиционной деятельности. Хотя это не исключает возможности применения и других методов. В частности, если инвестиции сопряжены с высокой степенью риска, инвесторы заинтересованы не столько в прибыльности проекта, сколько в том, чтобы инвестиции как можно быстрее окупили себя. Чем короче срок окупаемости, тем меньше степень риска инвестирования. В таком случае целесообразно применение метода, основанного на расчете срока окупаемости инвестиционных проектов с учетом ДДП.








