А1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
ЗАДАНИЕ: просмотрите видеофильмы, запишите КРАТКИЙ конспект тем, разберите задачи, задания на «4» и «5» - в конце каждой темы. Не забывайте: чертежи в тетрадях чертить карандашом и с помощью линейки. Готовые работы присылайте сообщением в ВК или на мой электронный адрес: agi1971@mail.ru.
Тема урока: "Аксиомы стереометрии и следствия из них"
«Стереометрия» - раздел геометрии, в котором изучаются фигуры в пространстве. В стереометрии, так же как и в планиметрии свойства геометрических фигур устанавливаются путём доказательства соответствующих теорем. При этом отправными являются свойства основных геометрических фигур, выражаемые аксиомами. «Аксиомы» - утверждения, содержащиеся в формулировках основных свойств простейших фигур, которые не требуют доказательства.
Основные фигуры в пространстве:
 Точка
Точка

 Прямая
Прямая
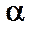 |
Плоскость
В стереометрии появляется новая фигура – плоскость. Плоскость - ровная поверхность (поверхность стола, доски), изображаемая в виде параллелограмма, обозначается греческими буквами 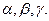 Введение нового геометрического образа – плоскости заставляет расширить систему аксиом. Поэтому вводим группу трёх аксиом, которая выражает основные свойства плоскостей в пространстве.
Введение нового геометрического образа – плоскости заставляет расширить систему аксиом. Поэтому вводим группу трёх аксиом, которая выражает основные свойства плоскостей в пространстве.
А1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

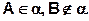
А2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой проходящей через эту точку.

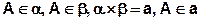
Чтобы построить этот чертёж, сначала строим плоскость 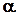 , затем проводим прямую а, от её концов две параллельные линии, так строим плоскость β. Обратите внимание, что невидимые линии проводим пунктиром.
, затем проводим прямую а, от её концов две параллельные линии, так строим плоскость β. Обратите внимание, что невидимые линии проводим пунктиром.
А3. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

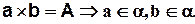
Следствия из аксиом стереометрии:
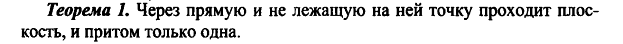
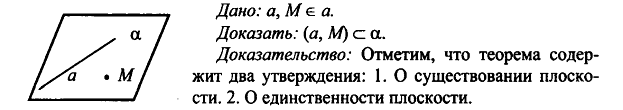

Задача 1. Точки A, B, C и D не лежат в одной плоскости. Докажите, что прямые AB и CD не пересекаются.
Дано: 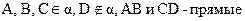
Доказать: 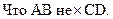
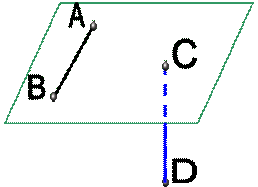
Доказательство: Предположим, что АВ пересекает СD, по аксиоме А3 через них можно провести плоскость, получаем что т.А, В, С, Д лежат в одной плоскости, но по условию точка D 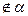 .Противоречие с условием. Следовательно, АВ не пересекает CD.
.Противоречие с условием. Следовательно, АВ не пересекает CD.
Задача 2. Точки А, В, С лежат в каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.
Дано: 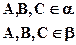 .
.
Доказать: 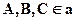 .
.

Доказательство: По аксиоме А2, если 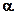 и
и 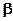
 имеют общую точку А, то они пересекаются по прямой а проходящей через эту точку. По условию, плоскости
имеют общую точку А, то они пересекаются по прямой а проходящей через эту точку. По условию, плоскости 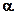 и
и 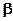 имеют три общие точки, следовательно, они пересекаются по прямой а, а точки
имеют три общие точки, следовательно, они пересекаются по прямой а, а точки 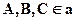 .
.
Задание на оценку «4» (любые 3 задания) и «5» (все задания).
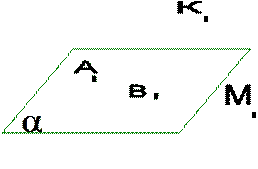
- Укажите точки, не принадлежащие плоскости
 .
.
- Определите может ли точка А лежать между точками В и С, если ВС=7.3 см., СА=6.5 см.
- Может ли луч спроходить между сторонами угла
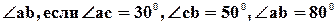 .
. - Треугольники АВС и РQR равны, известно, что АB=10cм., ВС=5см.,
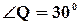 . Найти PQ, QR,
. Найти PQ, QR,  .
. - Пересекаются ли плоскости, если они не имеют ни одной общей точки?
Тема урока: Взаимное расположение двух прямых в пространстве.
| 
| 
|
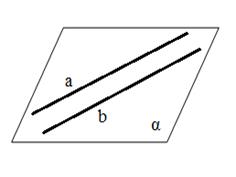
a 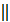 b , a b , a 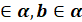
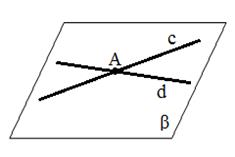
| c  d =А, c d =А, c 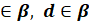
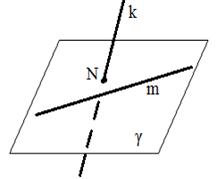
| k ∉ m , m 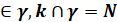
|
| лежат в одной плоскости | не лежат в одной плоскости | |
| параллельные прямые | пересекающиеся прямые | скрещивающиеся прямые |
Определение . Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.
Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Две прямые, имеющие лишь одну общую точку, называются пересекающимися.
Задание (для всех). Определите взаимное расположение прямых:
 А)
А)
|  В)
В)
|  С) С)
|
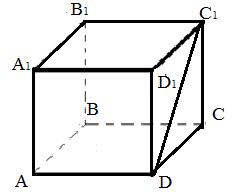
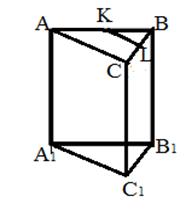
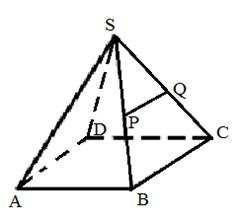
| АB ? CD AD ? DD1 DC ? A1D1 A1B1 ? A1D1 B1C1 ? BC B1C1 ? AA1 DC1 ? AB | АB ? CB AC ? A1C1 BC ? AA1 A1C1 ? KL KL ? BC CC1 ? KL AC ? BB1 | AB ? AD AD ? BC PQ ? SA AB ? SD AS ? CS PQ ?AB SB ? PQ |
Задания на «4» и «5»
Задача 1.
| Дано: PABC – тетраэдр. Параллельны ли его ребра PB и AC? Пересекаются ли прямые PC и AB? | 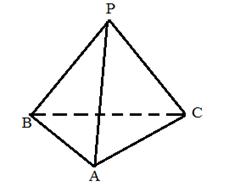
|
Задача 2.
Дано:
АВ 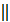 CD.
Могут ли быть прямые АC и ВD скрещивающимися?
Могут ли быть прямые АC и ВD пересекающимися? CD.
Могут ли быть прямые АC и ВD скрещивающимися?
Могут ли быть прямые АC и ВD пересекающимися?
| а)
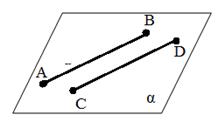 б)
б)
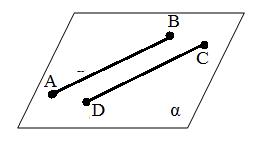
|
Задача 3.
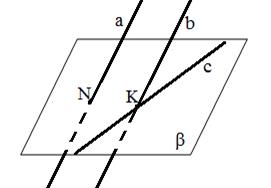
Нарисуйте плоскость 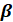 . Нарисуйте две параллельные прямые a и b, пересекающую данную плоскость. Нарисуйте прямую c лежащую в данной плоскости и пересекающую прямую b в точке K. Каково взаимное расположение прямых a и c? . Нарисуйте две параллельные прямые a и b, пересекающую данную плоскость. Нарисуйте прямую c лежащую в данной плоскости и пересекающую прямую b в точке K. Каково взаимное расположение прямых a и c?
| 
|
Задача 4.
| Дано: ABCDA1B1C1D1 - куб. | 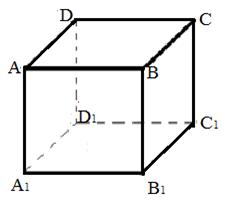
|
| 1) Определите взаимное расположение прямых: АВ и D1C1, BC и CC1, АB1 и B1C, AD и BB1, A1B и AD | 2) Определите взаимное расположение прямых: АD и D1C1, AA1 и CC1, АB1 и AC, A1D1 и BB1, BD и DD1 |








