Следствие (формула для вычетов в полюсах первого порядка).
1) Если 
– полюс функции 
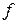первого порядка, то
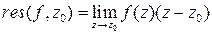
2) Если функци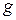и 
и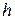 
аналитчны в окрестности точки , 
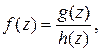
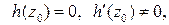то 
.
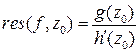Примеры.
1) Вычеты позволяют проводить разложение дробно-рациональной функции на простейшие. Рассмотрим для примера,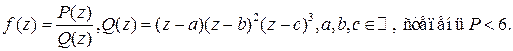 
Функцию 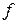можно разложить на простейшие
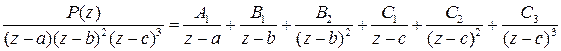
Коэффициенты разложения можно вычислить как вычеты в полюсах. Точка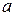 
является полюсом первого порядка, точка 
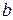-- полюс второго порядка, , точка 
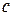-- полюс третьего порядка для функции 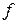, что позволяет вычислить 
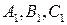. Точка 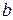– полюс первого порядка для функции 
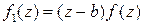. что позволяет вычислить 
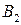, аналогично функция 
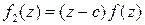позволяет найти 
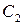и функция 
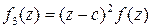позволяет найти 
.
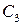2) Полученное в примере 1 разложение можно использовать для вывода формулы общего члена рекуррентной последовательности
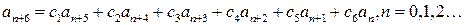
Эта последовательность определяет степенной ряд
,
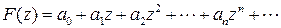который принято называть производящей функцией.
Обозначим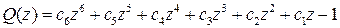 
.
Можно проверить, что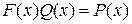 
, где
,
, 
, 
.
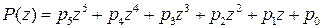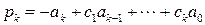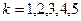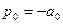Если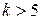 
, то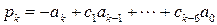 
, т. е. 
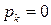в силу рекуррентного соотношения. Следовательно, 
.
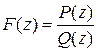Далее, для определенности, будем считать, что знаменатель имеет такое же разложение на множители, как в первом примере, т. е.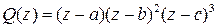 
. Тогда
.
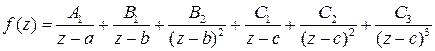Для получения нужной формулы достаточно разложить в степенные ряды слагаемые, и затем собрать вместе слагаемые с одинаковыми степенями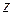 
.
Разложения для слагаемых получаются из формул:
, 
, 
,
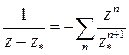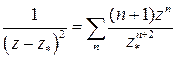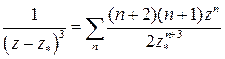Первая формула – сумма геометрической прогрессии, две другие получаются почленным дифференцированием первой.
7. Вычисление интегралов
Возможность «исправлять» контур интегрирования позволяет получить важную формулу для вычисления интегралов.
Теорема о вычетах. Пусть функция 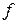аналитична в области 
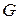за исключением конечного числа изолированных особых точек. Замкнутый положительно ориентированный контур 
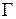лежит внутри области 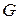, не проходит через особые точки функции 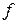и внутри контура содержатся особые точки 
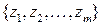. Тогда справедливо равенство
.
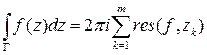Доказательство. Рассмотрим вспомогательный контур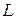 
, образованный контуром 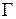, маленькими (не пересекающимися) окружностями 
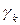с центрами в точках 
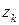и непересекающимися кривыми, соединяющими окружности с контуром 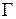, кривые проходятся по два раз в противоположных направлениях. Контур 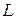не содержит внутри себя особых точек и по теореме Коши 
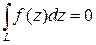. Рассуждая далее как в доказательстве теоремы о разложении в ряд Тейлора, можно показать, что
.
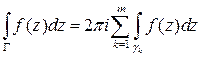Остается заметить, что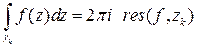 
.
Примеры вычисления интегралов
1) 
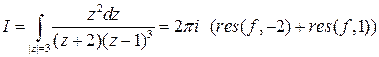
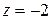– простой полюс, 
,
– 
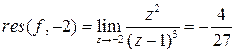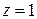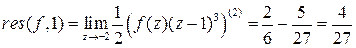, так как это полюс третьего порядка, следовательно, 
.
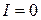2) 
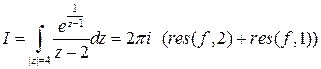
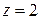– простой полюс, 
.
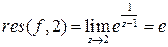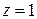– существенно особая точка, надо вычислять коэффициент 
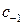из разложения в ряд Лорана. Это можно сделать, разлагая в ряды сомножители
,
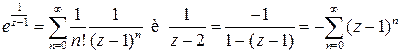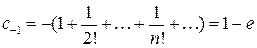это сумма произведений коэффициентов с индексами, дающими в сумме 
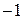, следовательно, 
.
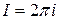Прямое применение теоремы о вычетах возможно для очень специального класса интегралов – по замкнутому контуру. Но, иногда замена переменой позволяет использовать эту технику для интегралов иного вида. Например, такая возможность появляется при интегрировании периодических функций по отрезку равному длине периода (замена переменной позволяет перевести интегрирование на окружность).
Интегрирование дробно-рациональных тригонометрических функций
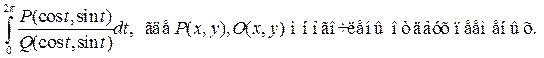
Замена переменной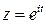 
позволяет свести задачу к теореме о вычетах. Действительно, при такой замене 
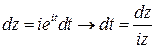, интегрирование будет происходить по окружности 
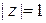, а функция под интегралом превратится в отношение многочленов 
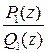, поскольку на окружности 
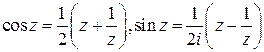. Возникший интеграл 
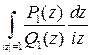можно вычислить с помощью теоремы о вычетах (все особые точки оказываются полюсами). Заметим, что это предполагает отсутствие корней на единичной окружности у многочлена 
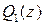, но если это условие нарушается, то возникающий несобственный интеграл расходится.
Пример.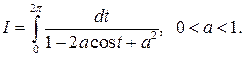 
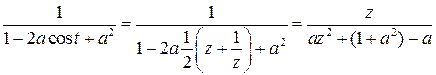
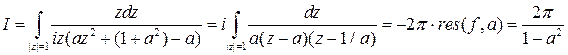
Хотя область применения этого методе довольно обширна, он скорее эффектен, чем эффективен и не дает существенных преимуществ в сравнении с универсальной тригонометрической заменой, кроме того, что сводит разложение на простейшие к вычислению вычетов.
Методы вычисления несобственных интегралов
Возможность применять вычеты для вычисления несобственных интегралов чрезвычайно важны, так как они дают уникальный инструмент для вычисления преобразований Фурье и Лапласа.
Неочевидна сама возможность применения теоремы о вычетах, для вычисления несобственных интегралов – отсутствует замкнутый контур. Но для того чтобы несобственный интеграл сходился необходимо, что бы функция была мала при больших значениях аргумента. Это дает надежду на то, что замыкание конура дугой окружности большого радиуса, мало изменит значение интеграла. Мы рассмотрим два класса функций, для которых легко обосновать возможность применение такого приема.
Интегралы от дробно рациональных функций
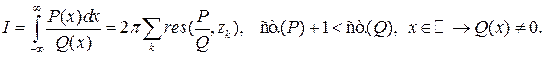
Здесь сумма распространяется по всем корням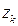 
многочлена 
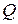в верхней полуплоскости.
Доказательство. Пусть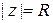 
окружность достаточно большого радиуса, такого, что все корни многочлена 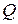лежат внутри нее, тогда на окружности будет выполнено неравенство 
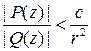. Обозначим через
,
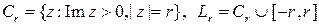тогда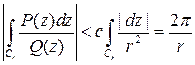 
, следовательно 
.
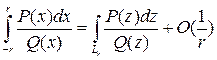Причем бесконечно малая добавка обращается в 0 при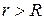 
, так как с этого момента прекращается изменение числа особых точек внутри контура 
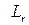, т.о.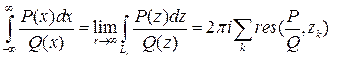 
Примеры
1) 
.
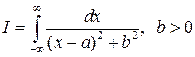Проверим условия применимости формулы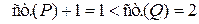 
.
Единственный корень многочлена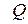 
в верхней полуплоскости 
.
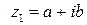Следовательно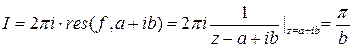 
.
2) 
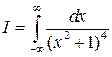
Единственный корень многочлена 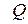в верхней полуплоскости 
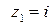. Для интегрируемой функции это полюс четвертого порядка. Следовательно
.
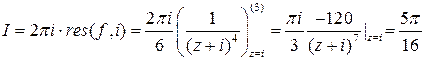Вычисление преобразования Фурье от дробно рациональных функций
,
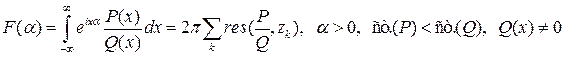здесь сумма распространяется по всем корням 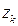многочлена 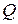в верхней полуплоскости. Небольшое отличие от первой формулы состоит в ослаблении требований к степеням многочленов, что существенно расширяет класс допустимых функций, продвигая формулу в трудном направлении.
Доказательство формулы опирается на вспомогательную оценку, которая имеет устоявшееся название.
Лемма Жордана. Пусть функция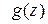 
непрерывна в област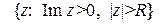и 
и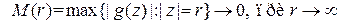 
, тогда 
.
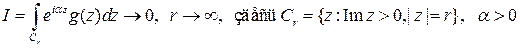Доказательство. Введем параметризацию на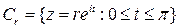 
.
Заметим, что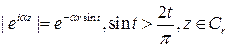 
и, следовательно
.
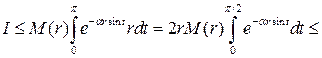
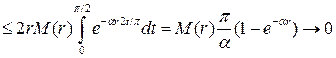Теперь доказательство формулу, может быть проведено также как в предыдущем случае.
Заметим, что условие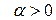 
можно заменить на 
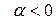, но при этом надо замыкать контур полуокружностью, лежащей в нижней полуплоскости.
Пример.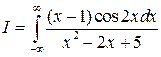 
.
Рассмотрим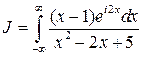 
, тогда 
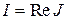, а интеграл 
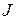можно вычислить по формуле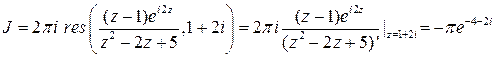 
Следовательно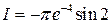 
.
Формула обращения преобразования Лапласа
Напомним определение преобразования Лапласа
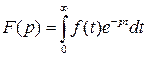
функция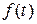 
должна удовлетворять следующими условиями:
1) на любом ограниченном интервале функция имеет конечное число разрывов первого рода и экстремумов,
2) 
,
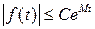3) 
.
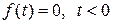Преобразование Фурье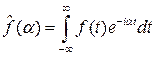 
и преобразование Лапласа тесно связаны 
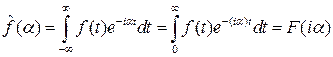. Теперь известная формула обращения преобразования Фурье может быть переписана для преобразования Лапласа
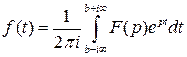
здесь предполагается, что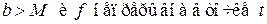 
. Поскольку формулу можно применять к любой функции (лишь бы интеграл сходился), то важно знать условия, гарантирующие, что функция 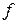принадлежит классу допустимых функций. Это обстоятельство важно при решении уравнений с помощью преобразования Лапласа. Зная лемму Жордана нетрудно получить достаточные условия [4] .
Теорема. Если функция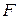 
аналитична в полуплоскост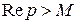и 
и
1) 
,
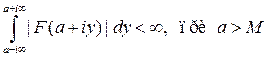2) 
,
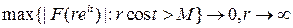то 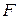является изображением функции 
.
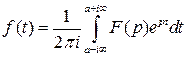Следствие. (Формула восстановления оригинала.) Если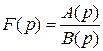 
,
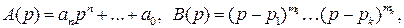
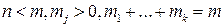то 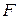является изображением функции
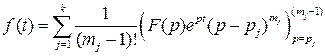
Если все корни простые (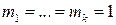 
), то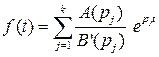 
.
Список литературы
1. Комплексные числа и многочлены: Методические указания к решению задач. сост./Абрамова М.Н., Толкачева Е.А., Куприянов А.И. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2006.
2. Лаврентьев М.А., Шабат Б.И. Методы теории функций комплексного переменного. М.: ФМЛ,1965.
3. Смирнов В.И. Курс Высшей Математики, т.3, ч.2, СПб.: BHV, 2008.
4. Сидоров Ю.В., Федорюк М.В., Шабунин М.И. Лекции по теории функций комплексного переменного. М.: ФМЛ,1982.
Оглавление
Элементарные функции комплексного переменного . . . . . . . . . . . . . . . . . . . 3
Условия дифференцируемости функции комплексного переменного . . . . . . 8
Интегрирование аналитических функций . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
Теорема единственности. Аналитическое продолжение . . . . . . . .. . . . . . . . . 16
Особые точки. Ряды Лорана . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . 17
Вычеты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
Вычисление интегралов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . .32
Редактор
Подписано в печать Формат 60х84 1/16
Бумага офсетная. Печать офсетная. Печ. Л.
Гарнитура « «. Тираж экз. Заказ
Издательство СПбГЭТУ «ЛЭТИ»
197376, С.-Петербург, ул.Проф. Попова, 5