Аналитическое продолжение
Аналитические функции, в некоторых отношениях, очень похожи на многочлены.
Теорема. Нули аналитической функции, отличной от тождественного нуля, изолированы, т. е. у каждой точки, где аналитическая функция обращается в ноль, существует окрестность, не содержащая других нулей этой функции.
Доказательство. Пусть функция 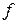 аналитична в окрестности точки
аналитична в окрестности точки  и
и 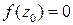 , тогда найдется достаточно малый круг
, тогда найдется достаточно малый круг 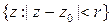 , в котором функция допускает разложение в ряд Тейлора. Из предположения
, в котором функция допускает разложение в ряд Тейлора. Из предположения 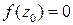 следует, что
следует, что 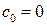 , но поскольку функция не равна нулю тождественно, то существуют ненулевые коэффициенты. Пусть
, но поскольку функция не равна нулю тождественно, то существуют ненулевые коэффициенты. Пусть 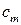 – первый из них, тогда ряд Тейлора этой функции можно представить в виде
– первый из них, тогда ряд Тейлора этой функции можно представить в виде
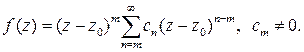
Можно подобрать число 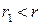 такое, что в круге
такое, что в круге 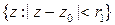 выполнено неравенство
выполнено неравенство 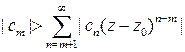 и, следовательно, в этом круге функция имеет единственный корень
и, следовательно, в этом круге функция имеет единственный корень  .
.
Основная теорема алгебры утверждает, что многочлен 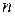 -й степени имеет
-й степени имеет 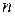 корней. Аналитическая функция, как многочлен «бесконечной» степени может иметь бесконечное число корней, например,
корней. Аналитическая функция, как многочлен «бесконечной» степени может иметь бесконечное число корней, например, 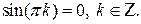 Но на расположение корней имеется жесткое ограничение: они не могут сгущаться.
Но на расположение корней имеется жесткое ограничение: они не могут сгущаться.
Теорема единственности. Если функция 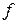 является аналитической в области
является аналитической в области 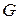 и
и 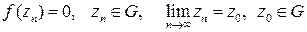 , то
, то 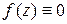 .
.
Доказательство. В силу непрерывности 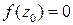 , и точка
, и точка  оказывается корнем функции, в любой окрестности которого имеются другие корни. Такое возможно только для
оказывается корнем функции, в любой окрестности которого имеются другие корни. Такое возможно только для 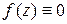 .
.
Рассмотрим теперь свойства аналитических функций, которые не возможны для многочленов.
Определение. Если функция 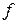 является аналитической в круге круг
является аналитической в круге круг 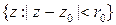 и
и 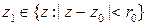 , то существует число
, то существует число 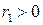 такое, что
такое, что 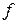 разлагается в ряд Тейлора в круге
разлагается в ряд Тейлора в круге 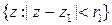 . Если эту процедуру можно продолжать и за конечное число шагов перейти в точку
. Если эту процедуру можно продолжать и за конечное число шагов перейти в точку  , то говорят, что функция
, то говорят, что функция 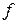 допускает аналитическое продолжение из точки
допускает аналитическое продолжение из точки  в точку
в точку 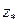 .
.
Разумеется, такая процедура для многочленов возможна всегда, но для аналитических функций общего вида это не так. Функцию 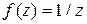 не возможно продолжить из точки
не возможно продолжить из точки 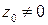 в точку
в точку 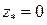 . Более того, вполне благополучную в кольце
. Более того, вполне благополучную в кольце 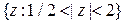 функцию
функцию 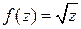 можно продолжать из точки
можно продолжать из точки 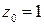 и вернуться в ту же точку
и вернуться в ту же точку 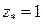 , но при этом окажется, что значение функции будет другим. Процедура аналитического продолжения выводит на многолистные аналитические функции. Это полезные и важные объекты, познакомится с ними можно по книге [3].
, но при этом окажется, что значение функции будет другим. Процедура аналитического продолжения выводит на многолистные аналитические функции. Это полезные и важные объекты, познакомится с ними можно по книге [3].
Рассмотренные свойства составляют исчерпывающую картину поведения аналитической функции во внутренних точках области аналитичности. Теперь следует обратиться к рассмотрению точек, где аналитичность нарушается.
5. Особые точки. Ряды Лорана
Функция аналитическая в точке обязательно аналитична в некоторой окрестности этой точки, но это не означает, что функцию можно продолжить в любую точку, двигаясь от окрестности к окрестности. Дело в том, что размер окрестности может очень маленьким. Рассмотрим пример того, как может «исчезать» аналитичность: функция 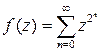 сходится при любом
сходится при любом 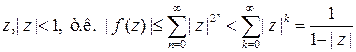 , но если положить
, но если положить 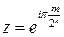 , то ряд разойдется, поскольку
, то ряд разойдется, поскольку 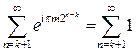 . Поведение аналитической функции при приближении к границе области аналитичности может быть очень сложным, эти вопросы выходят далеко за рамки вводного курса.
. Поведение аналитической функции при приближении к границе области аналитичности может быть очень сложным, эти вопросы выходят далеко за рамки вводного курса.
Другая причина потери аналитичности связана с невозможностью определить функцию, как однозначную в окрестности точки. Нельзя отказаться от рассмотрения этой ситуации, потому что она возникает при решении такой банальной задачи, как квадратное уравнение. Рассмотрим функцию 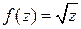 . Напомним, что можно определить корень двумя способами (две ветви корня)
. Напомним, что можно определить корень двумя способами (две ветви корня)
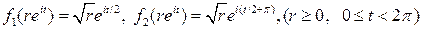
Вычислим значения 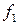 в двух близких точках
в двух близких точках
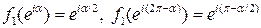
Если 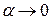 , то оба аргумента стремятся к 1, но значения функций стремятся соответственно к 1 и -1. Такого рода точки называют точками ветвления.
, то оба аргумента стремятся к 1, но значения функций стремятся соответственно к 1 и -1. Такого рода точки называют точками ветвления.
Здесь будет рассмотрен только простейший вариант нарушения аналитичности.
Определение. Точка  называется изолированной особой точкой функции, если существует число
называется изолированной особой точкой функции, если существует число 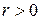 такое, что в «проколотом круге»
такое, что в «проколотом круге» 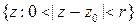 функция аналитична и однозначна, т.е. любое аналитическое продолжение функции вдоль замкнутой кривой сохраняет значение функции в стартовой точке.
функция аналитична и однозначна, т.е. любое аналитическое продолжение функции вдоль замкнутой кривой сохраняет значение функции в стартовой точке.
Не приходится ожидать, что в окрестности изолированной особой точки функцию удастся разложить в ряд Тейлора, но представить функцию виде ряда более сложного вида всегда возможно.
Определение. Рядом Лорана называется следующее выражение:
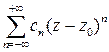
Говорят, что ряд Лорана сходится в кольце 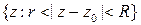 , ряд
, ряд 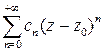 сходится при
сходится при 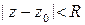 , а ряд
, а ряд 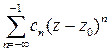 сходится при
сходится при 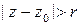 .
.
Примеры. 1) Исследуем сходимость ряда Лорана 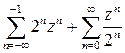 . Перепишем ряды в более привычной форме
. Перепишем ряды в более привычной форме 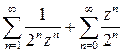 . Первый ряд сходится при
. Первый ряд сходится при 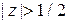 , второй при
, второй при 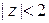 , т. о. ряд Лорана сходится в кольце
, т. о. ряд Лорана сходится в кольце 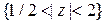 .
.
2) «Похожий» ряд 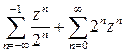 расходится, т. к. ряд
расходится, т. к. ряд 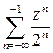 сходится при
сходится при 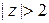 , а ряд сходится только при
, а ряд сходится только при 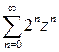
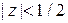 .
.
Введенной конструкции достаточно, что бы разложить в ряд любую аналитическую функцию в окрестности изолированной особой точки.
Теорема. (о разложении в ряд Лорана) Если  – изолированная особая точка функции
– изолированная особая точка функции 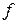 , то в проколотой окрестности точки
, то в проколотой окрестности точки  она допускает разложение в ряд Лорана
она допускает разложение в ряд Лорана
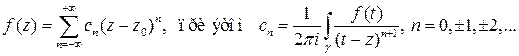
План доказательства. Фиксируем точку 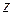 . Рассмотрим пару окружностей, лежащих внутри кольца и таких, что точка
. Рассмотрим пару окружностей, лежащих внутри кольца и таких, что точка 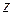 лежит между ними:
лежит между ними:

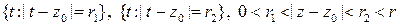 .
.
Соединим окружности отрезком, не проходящим через точку 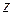 , и сформируем из них положительно ориентированный контур, обходящий точку
, и сформируем из них положительно ориентированный контур, обходящий точку 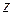 в положительном направлении и не содержащий внутри себя особых точек функции
в положительном направлении и не содержащий внутри себя особых точек функции 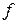 . Представим
. Представим 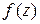 с помощью формулы Коши и применим рассуждение, использованное в доказательстве теоремы о разложении в ряд Тейлора. На внешней окружности оно пройдет без изменений (важно, что
с помощью формулы Коши и применим рассуждение, использованное в доказательстве теоремы о разложении в ряд Тейлора. На внешней окружности оно пройдет без изменений (важно, что 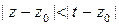 ) и получится часть ряда Лорана с положительными коэффициентами. На внутренней окружности справедливо противоположное неравенство
) и получится часть ряда Лорана с положительными коэффициентами. На внутренней окружности справедливо противоположное неравенство 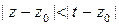 , что изменит ход тождественных преобразований и даст, в результате часть ряда Лорана с отрицательными коэффициентами.
, что изменит ход тождественных преобразований и даст, в результате часть ряда Лорана с отрицательными коэффициентами.
Поведение функции в окрестности изолированной особой точки может быть различным. Эти различия хорошо улавливаются следующим определением.
Определение. Классификация изолированных особых точек.
Пусть  -- изолированная особая точка функции
-- изолированная особая точка функции 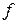 .
.
 называют устранимой особой точкой, если функция ограничена в проколотом круге
называют устранимой особой точкой, если функция ограничена в проколотом круге 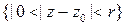 ,
,
 называют полюсом, если
называют полюсом, если 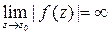 ,
,
 называют существенной особой точкой во всех остальных случаях.
называют существенной особой точкой во всех остальных случаях.
Примеры.
1) для функции 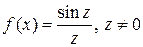 , точка
, точка 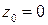 является устранимой особой точкой,
является устранимой особой точкой,
2) для функции 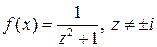 , точки
, точки 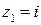 и
и 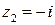 являются полюсами,
являются полюсами,
3) для функции 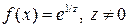 , точка
, точка 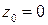 является существенно особой точкой, действительно,
является существенно особой точкой, действительно, 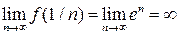 и, следовательно, функция не ограничена,
и, следовательно, функция не ограничена, 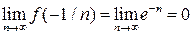 , следовательно, функция не имеет предела в точке
, следовательно, функция не имеет предела в точке  .
.
Проследим, как выглядят ряды Лорана в каждом из этих случаев
1) 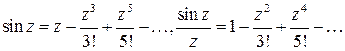
2) 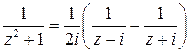 чтобы получить ряд Лорана в изолированной особой точке
чтобы получить ряд Лорана в изолированной особой точке 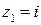 достаточно разложить в ряд второе слагаемое
достаточно разложить в ряд второе слагаемое
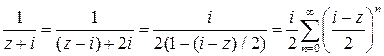
Следовательно
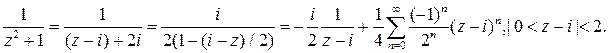
3) 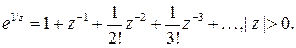
Внешне банальная, классификация особых точек приобретает глубокий смысл благодаря замечательной связи с рядами Лорана.
Теорема (об эквивалентной классификации). Пусть  – изолированная особая точка функции
– изолированная особая точка функции 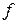 ,
, 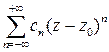 – ее ряд Лорана. Тогда:
– ее ряд Лорана. Тогда:
1)  – устранимая особая точка
– устранимая особая точка 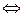
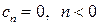 (ряд Лорана не содержит слагаемых с отрицательными степенями);
(ряд Лорана не содержит слагаемых с отрицательными степенями);
2)  – полюс
– полюс 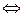 существует число
существует число 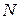 такое, что
такое, что 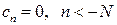 (ряд Лорана содержит конечное число слагаемых с отрицательными степенями);
(ряд Лорана содержит конечное число слагаемых с отрицательными степенями);
3)  – существенно особая точка
– существенно особая точка 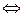 для всякого положительного числа
для всякого положительного числа 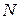 существует
существует 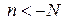 такое, что
такое, что 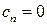 (ряд Лорана содержит бесконечное число слагаемых с отрицательными степенями).
(ряд Лорана содержит бесконечное число слагаемых с отрицательными степенями).
Для доказательства теоремы потребуется простая, но полезная оценка:
Неравенство Коши
Если функция 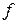 аналитична в круге
аналитична в круге 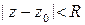 и
и 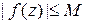 при
при 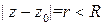 , то
, то 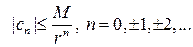
Доказательство неравенства. В теореме о разложении в ряд Лорана доказано, что 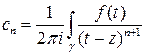 . В качестве контура интегрирования можно взять окружность
. В качестве контура интегрирования можно взять окружность 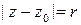 , далее простые оценки по модулю завершают доказательство.
, далее простые оценки по модулю завершают доказательство.
Доказательство теоремы об эквивалентной классификации.
1) Из условия равенства нулю коэффициентов с отрицательными номерами следует аналитичность функции в круге 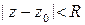 , и, следовательно, она ограничена в этом круге, т. е.
, и, следовательно, она ограничена в этом круге, т. е.  -- устранимая особая точка.
-- устранимая особая точка.
Покажем, что верно и обратное. Пусть 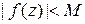 в
в 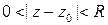 .
.
Воспользуемся неравенством Коши 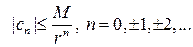 при любом
при любом 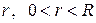 . Для отрицательных
. Для отрицательных 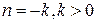 получим
получим 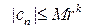 , поскольку
, поскольку 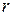 может быть сколь угодно малым, то
может быть сколь угодно малым, то 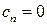 .
.
2) Предположим, что существует положительное число 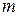 такое, что
такое, что 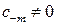 и
и  . Тогда свойства степенных функций, гарантируют, что в достаточно малой окрестности точки
. Тогда свойства степенных функций, гарантируют, что в достаточно малой окрестности точки  справедлива оценка
справедлива оценка 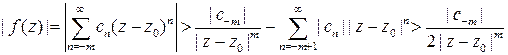 . Следовательно
. Следовательно  -- точка полюса.
-- точка полюса.
Проверим обратное утверждение. Если известно, что  -- точка полюса, то
-- точка полюса, то 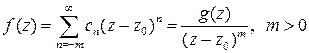 , причем
, причем 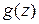 аналитическая функция и
аналитическая функция и 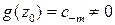 . Можно доказать, что в этих условиях функция
. Можно доказать, что в этих условиях функция 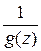 также является аналитической. Это следует из следующего простого свойства степенных рядов: если степенной ряд
также является аналитической. Это следует из следующего простого свойства степенных рядов: если степенной ряд 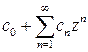 сходится при
сходится при 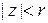 и
и 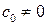 , то
, то 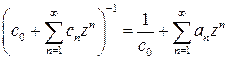 и ряд сходится при
и ряд сходится при 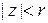 .
.
С учетом этого утверждения 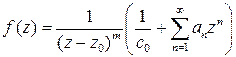 и очевидно
и очевидно 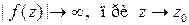 .
.
3) Достаточно, заметить, что если модуль функции не ограничен и не стремится к бесконечности, то он не может иметь предела. Аналогично доказывается обратное утверждение.
6. Вычеты
Наиболее востребованное приложения рядов Лорана связано с формулой для вычисление коэффициента 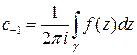 , здесь
, здесь 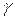 – контур, обходящий особую точку
– контур, обходящий особую точку  в положительном направлении и не содержащий внутри других особых точек. Дело в том, что коэффициенты ряда часто удается определить из косвенных соображений, и тогда формула становиться мощным инструментом для вычисления контурных интегралов. Если известен коэффициент
в положительном направлении и не содержащий внутри других особых точек. Дело в том, что коэффициенты ряда часто удается определить из косвенных соображений, и тогда формула становиться мощным инструментом для вычисления контурных интегралов. Если известен коэффициент 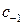 , то известен и интеграл. Для устранимых особых точек этот коэффициент равен нулю и получается уже известная теорема Коши. Будет показано, что в точках полюсов вычисление коэффициента
, то известен и интеграл. Для устранимых особых точек этот коэффициент равен нулю и получается уже известная теорема Коши. Будет показано, что в точках полюсов вычисление коэффициента 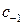 дело чисто техническое. Это дает аппарат для вычисления множества интегралов. В существенно особых точках мало шансов получить
дело чисто техническое. Это дает аппарат для вычисления множества интегралов. В существенно особых точках мало шансов получить 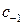 из косвенных соображений, но если это все-таки удается, то результаты получаются наиболее эффектные. Роль коэффициента
из косвенных соображений, но если это все-таки удается, то результаты получаются наиболее эффектные. Роль коэффициента 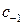 в этих вопросах так велика, что для него существует стандартное обозначение.
в этих вопросах так велика, что для него существует стандартное обозначение.
Определение. Пусть  -- изолированная особая точка функции
-- изолированная особая точка функции 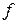 , тогда вычетом функции
, тогда вычетом функции 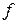 в точке
в точке  называют
называют 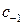 , и обозначают это символом
, и обозначают это символом 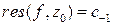 .
.
Используя это обозначения можно записать формулу
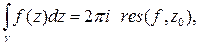
здесь, как и прежде, 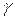 -- контур, обходящий особую точку
-- контур, обходящий особую точку  в положительном направлении и не содержащий внутри других особых точек. Чтобы сделать эту формулу содержательной, надо указать косвенный способ вычисления вычетов. Как было отмечено, это можно сделать, если
в положительном направлении и не содержащий внутри других особых точек. Чтобы сделать эту формулу содержательной, надо указать косвенный способ вычисления вычетов. Как было отмечено, это можно сделать, если  является полюсом. Для этого нам потребуется уточнение определения, фактически содержащееся в доказательстве теоремы о классификации особых точек.
является полюсом. Для этого нам потребуется уточнение определения, фактически содержащееся в доказательстве теоремы о классификации особых точек.
Определение. Пусть  – полюс функции
– полюс функции 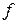 , тогда порядком полюса
, тогда порядком полюса
называется число 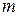 такое, что
такое, что  и
и 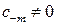 .
.
Теорема (формула вычисления вычетов в полюсах). Если  – полюс функции
– полюс функции 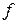 порядка
порядка 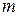 , то
, то
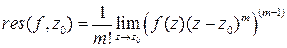
Доказательство. Из определения полюса следует, что
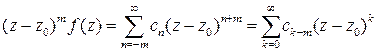 .
.
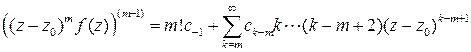
Следовательно 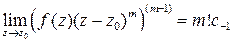 .
.








