Теория функций комплексной переменной
Федеральное агентство по образованию
___________________________________
Санкт-Петербургский государственный
Электротехнический университет «ЛЭТИ»
_______________________________________
Теория функций комплексной переменной
Методические указания
к практическим занятиям
по высшей математике
Санкт-Петербург
Издательство СПбГЭТУ «ЛЭТИ»
2010
УДК 512.64(07)
ТФКП: Методические указания к решению задач / сост.: В.Г.Дюмин, А.М.Коточигов, Н.Н.Сосновский.СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2010. 32с.
Содержат примеры решения основных типов задач ТФКП, ориентированных на выполнение заданий, формирующих оценку текущего контроля по этой дисциплине. Предназначены для студентов ФКТИ всех специальностей.
Утверждено
редакционно-издательским советом университета
в качестве методических указаний
© СПбГЭТУ «ЛЭТИ», 2010
Функции комплексного переменного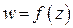 
, 
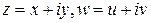, в общем случае отличаются от отображений вещественной плоскости 
в себя 
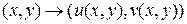только формой записи. Важным и чрезвычайно полезным объектом оказывается класс функции комплексного переменного,
имеющих производную такую же, как и функции одной переменной. Известно, что функции нескольких переменных могут иметь частные производные и производные по направлению, но, как правило, производные по разным направлениям не совпадают, и говорить о производной в точке не возможно. Однако для функций комплексной переменной удается описать условия, при которых они допускают дифференцирование. Изучение свойств дифференцируемых функций комплексного переменного составляет содержании методических указаний. Указания ориентированны на демонстрацию того, как свойства таких функций могут быть использованы для решения разнообразных задач. Успешное освоение, излагаемого материала невозможно без элементарных навыков вычислений с комплексными числами и знакомства с простейшими геометрическими объектами, определяемыми в терминах неравенств, связывающих вещественную и мнимую часть комплексного числа, а так же его модуль и аргумент. Краткое изложение всех необходимых для этого сведений можно найти в методических указаниях [1].
Стандартный аппарат математического анализа: пределы, производные, интегралы, ряды широко используется в тексте методических указаний. Там, где эти понятия имеют свою специфику, по сравнению с функциями одной переменной, приведены соответствующие пояснения, но в большинстве случаев достаточно разделить вещественную и мнимую часть и применить к ним стандартный аппарат вещественного анализа.
1. Элементарные функции комплексного переменного
Обсуждение условий дифференцируемости функций комплексного переменного, естественно начать с выяснения того, какие элементарные функции обладают этим свойством. Из очевидного соотношения
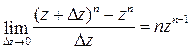
Вытекает дифференцируемость любого многочлена. И, поскольку, степенной ряд можно дифференцировать почленно внутри круга его сходимости,
то любая функция дифференцируема в точках, в окрестности которых ее можно разложить в ряд Тейлора. Это достаточное условие, но, как вскоре выясниться, оно является и необходимым. Исследование функций одной переменной по производной удобно поддерживать, контролируя поведение графика функции. Для функций комплексного переменного такой возможности нет. Точки графика лежат в пространстве размерности 4, 
.
Тем не менее, некоторое графическое представление о функции можно получить, рассматривая образы достаточно простых множеств комплексной плоскости 
, возникающие под воздействием заданной функции. Для примера, рассмотрим, с этой точки зрения несколько простых функций.
Линейная функция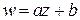 
Эта простая функции очень важна, тек как любая дифференцируемая функция локально похожа на линейную. Рассмотрим действие функции с максимальной подробностью
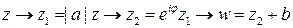
здесь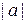 
-- модуль комплексного числа 
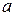и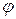 
-- его аргумент. Таким образом, линейная функция осуществляет растяжение, поворот и сдвиг. Следовательно, линейное отображение переводит любое множество в подобное множество. В частности, под воздействием линейного отображения прямые переходят в прямые, а окружности в окружности.
Функция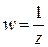 
Эта функция -- следующая по сложности за линейной. Трудно ожидать, что она переведет любую прямую в прямую, а окружность в окружность, простые примеры показывают, что этого не происходит, тем не менее, можно показать, что эта функция переводит множество всех прямых и окружностей в себя. Чтобы убедится в этом, удобно перейти к вещественному (координатному) описанию отображения
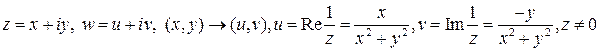
Для доказательства потребуется описание обратного отображения
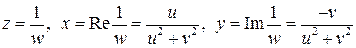
Рассмотрим уравнение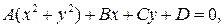 
если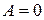 
, то получится общее уравнение прямой. Если 
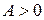, то
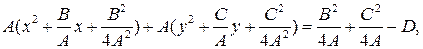
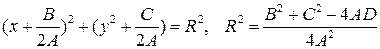
Следовательно, при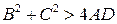 
получается уравнение произвольной окружности.
Отметим, что есл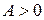и и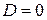 
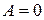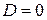, то окружность проходит через начало координат. Если же и , то получится прямая, проходящая через начало координат.
Под действие инверсии рассматриваемое уравнение перепишется в виде
, ( 
)
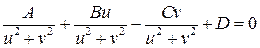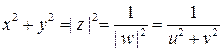или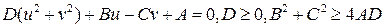 
. Видно, что это тоже уравнение, описывающие либо окружности, либо прямые. То, что в уравнении коэффициенты 
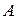и 
поменялись местами, означает, что при инверсии прямые, проходящие через 0, перейдут в окружности, а окружности, проходящие через 0, перейдут в прямые.
Степенные функции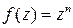 
Главное отличие этих функцией от рассмотренных ранее состоит в том, что они не являются взаимно однозначными (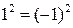 
). Можно сказать, что функция 
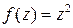переводит комплексную плоскость в два экземпляра той же плоскости. Аккуратное рассмотрение этой темы требует использования громоздкого аппарата римановых поверхностей и выходит за рамки рассматриваемых здесь вопросов. Важно понимать, что комплексную плоскость можно разделить на секторы, каждый из которых взаимно однозначно отображается на комплексную плоскость. Это разбиение для функции 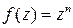выглядит так, 
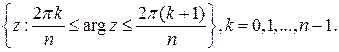Например, верхняя полуплоскость взаимно однозначно отображается на комплексную плоскость функцией 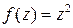. Искажения геометрии для таких изображений описать сложнее, чем в случае инверсии. В качестве упражнения можно проследить, во что переходит сетка прямоугольных координат верхней полуплоскости при отображении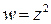 
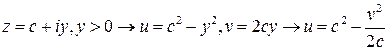
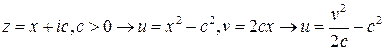
Видно, что сетка прямоугольных координат переходит в семейство парабол, образующих систему криволинейных координат в плоскости 
. Описанное выше разбиение плоскости таково, что функция 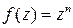отображает каждый из 
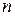секторов на всю плоскость. Описание прямого и обратного отображения выглядит так
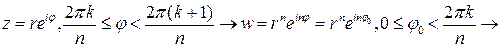
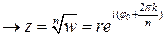
Таким образом, функция 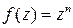имеет 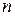различных обратных функций,
заданных в различных секторах плоскости
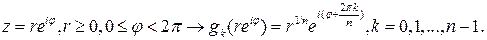
В таких случаях говорят, что отображение многолистно.
Функция Жуковского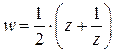 
Функция имеет собственное названия, поскольку она составила основу теории крыла летательного аппарата, созданную Жуковским (описание этой конструкции можно найти в книге [2]). Функция обладает рядом интересных свойств, остановимся на одном из них – выясним, на каких множествах эта функция действует взаимнооднозначно. Рассмотрим равенство
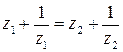, откуда 
.
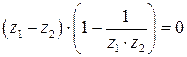Следовательно, функция Жуковского взаимнооднозначна в любой области, в которой для любых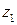 
и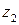 
их произведение не равно единице. Таковыми являются, например, открытый единичный круг 
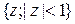и дополнение замкнутого единичного круга 
.
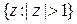Рассмотрим действие функции Жуковского на окружности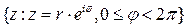 
, тогда
.
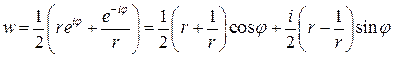Разделяя вещественную и мнимую части, получим параметрическое уравнение эллипса
, 
.
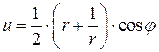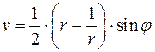Если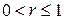 
, то эти эллипсы заполняют всю плоскость. Аналогично проверяется, что образами отрезков 
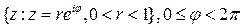являются гиперболы
.
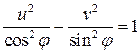Показательная функция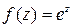 
Функция допускает разложение в степенной ряд, абсолютно сходящийся во всей комплексной плоскости, следовательно, она всюду дифференцируема. Опишем множества, на которых функция взаимнооднозначна. Очевидное равенство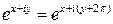 
показывает, что плоскость можно разбить на семейство полос 
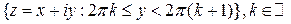, каждую из которых функция взаимнооднозначно отображает на всю комплексную плоскость. Это разбиение существенно для того, что бы понять, как устроена обратная функция, точнее обратные функции. На каждой из полос естественным образом определено обратное отображение
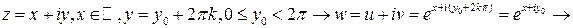
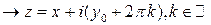
Обратная функция и в этом случае многолистна, причем количество обратных функций бесконечно.
Геометрическое описание отображения довольно простое: прямые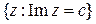 
переходят в лучи 
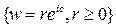, отрезки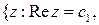 
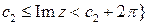переходят в окружности 
.
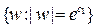2. Условия дифференцируемости
функции комплексного переменного
Выясним условия, гарантирующие наличие производной у функции комплексного переменного, т. е. наличие предела
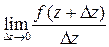
Рассмотрим эквивалентное «вещественное» описание этого вопроса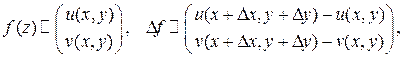 
.
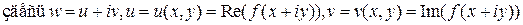Если устремить приращения аргументов к нулю, то получится следующее соотношение для дифференциалов
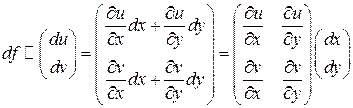
Требуется выяснить, при каких условиях найдется комплексное число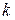 
такое, что 
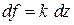, т. е.
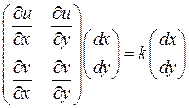
Заметим, что умножение вектора на комплексное число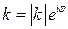 
означает растяжение с коэффициентом 
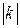и поворот на угол 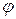. Воспользуемся матричным описание этих действий и получим равенство
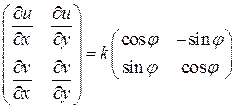
Из этого равенства следует требуемое условие, которое можно сформулировать в виде теоремы.
Теорема (условие Коши-Римана). Функция комплексного переменного дифференцируема тогда и только тогда, когда выполнены равенства
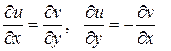– условия Коши-Римана.
Определение. Функция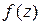 
называется аналитической в области 
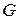, если в каждой точке области выполнено условие Коши-Римана.
Напомним, что областью называется любое подмножество комплексной плоскости такое, что каждая точка входит в него вместе с окрестностью (достаточно малым кругом с центром в этой точке).
Легко привести примеры функций удовлетворяющих условию Коши-Римана в одной единственной точке, но важными являются именно аналитические функции. Только о них и будет идти речь в дальнейшем.
Из анализа доказательства условий Коши-Римана вытекает полезная геометрическая интерпретация: в малой окрестности точки аналитическая функция действует как линейная, при этом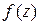 
– сдвиг, 
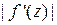– локальный коэффициент растяжения, а 
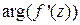– локальный угол поворота, осуществляемый отображением 
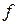в точке 
.
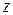Следствие. Пусть функция 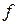аналитическая в области 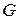тогда
1) если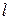 
кривая в област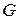и , и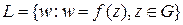 
, то длина кривой 
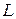равна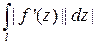 
(кривая 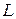получается из кривой 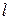«растяжением», коэффициент растяжение в точке 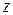равен ).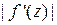
2) если область 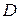содержится в област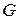и , и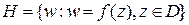 
, то площадь области 
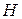равна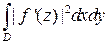 
, (локальный коэффициент растяжения одинаков во всех направлениях, поэтому квадрат со стороной 
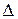перейдет в квадрат со стороной 
).
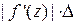3) если две кривые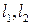 
лежат в области 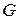, пересекаются в точке 
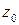под углом 
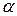(т. е. касательные к кривым в этой точке образуют угол 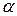), то образы этих кривых при отображении 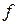пересекаются в точке 
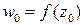под тем же углом .
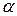Задача. Покажите, что элемент дуги кривой 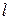равен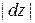 
. Указание. Рассмотрите параметрическое описание кривой 
.
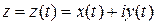Примеры. 1) Вычислим длину образа отрезка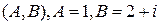 
при отображении 
.
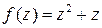Решение.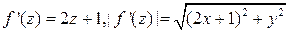 
, для вычисления интеграла надо ввести параметризацию кривой
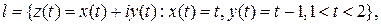
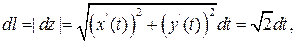
Теперь можно вычислить длину образа
.
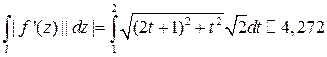2) Вычислим площадь образа квадрата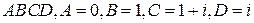 
при отображении 
.
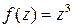Решение.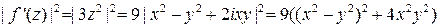 
,
площадь равна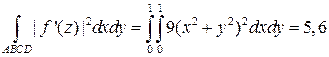 
.
3) Образ квадрата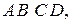 
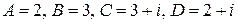при дробно-линейном отображении
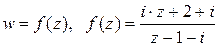
Чтобы контролировать отображения надо выяснить, во что перейдут прямые, составляющие границы квадрата. Эта задача сводится к рассмотренной ранее инверсии, если предварительно разложить дробно-линейную функцию на компоненты
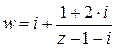
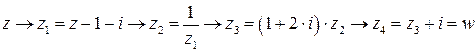
Обозначим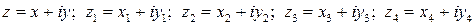 
. Действительная часть - x и мнимая часть - y с соответствующими индексами являются координатами образов точки z, получаемых в результате последовательных преобразований.
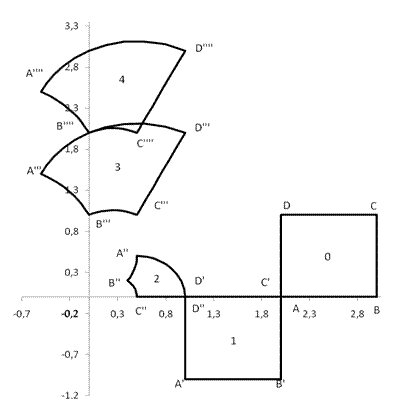
Построим изображения квадрата, выписывая формулы преобразования координат для каждого шага (Рис.1). Вершины квадрата и их последовательные образы будем обозначать одними и теми же буквами с соответствующим количеством штрихов на каждом изображении. Так,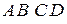 
это вершины исходного квадрата, 
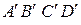- вершины квадрата после первого шага отображения и т.д. Цифра внутри квадрата обозначает номер преобразования, 0 – исходный квадрат. Вообще говоря, квадрат будет получаться криволинейным, но углы при вершинах будут оставаться прямыми. Будет также сохраняться ориентация квадрата: внутренность квадрата на каждом изображении будет находиться слева от точки, движущейся по границе в направлении от 
к 
.
Шаг 1. Формулы преобразования координат:
.
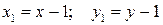Это преобразование задает параллельный перенос исходного квадрата вниз и влево на единицу.
Шаг 2. Формулы преобразования координат:
.
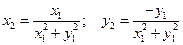Данное преобразование задает инверсию. Заметим, что отрезк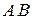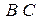и 
, 
и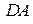 
переходят в дуги окружностей, а отрезок 
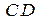сохраняется прямолинейным, точка 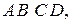остается неподвижной.
Шаг 3. Формулы преобразования:
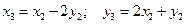
Это преобразование задает поворот вокруг начала координат на угол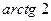 
против часовой стрелки и растяжение в 
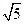раз.
Шаг 4. Формулы преобразования координат:
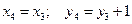
Это преобразование задает сдвиг на единицу вверх по оси y.
4) Вычислим периметры последовательных изображений квадрата 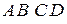из предыдущего примера, обозначения сохраняются.
Периметр изображения 1 равен периметру изображения 0: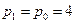 
.
Вычислим периметр изображения 2 – криволинейного квадрата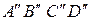 
:
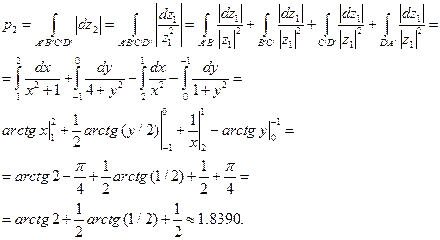
Изображение 3 получается из изображения 2 поворотом и растяжением в 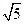раз, а изображение 4 – сдвигом изображения 3. Поэтому
.
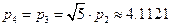3. Интегрирование аналитических функций
В рамках рассматриваемых здесь вопросов важны криволинейные интегралы второго рода от функции комплексного переменного. Такой интеграл не требует специального определения, так как он легко сводится к паре криволинейных интегралов от функций вещественного переменного:
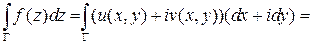
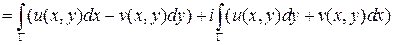
для вычисления, которых требуется провести параметризацию кривой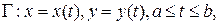 
и вычислить определенные интегралы:
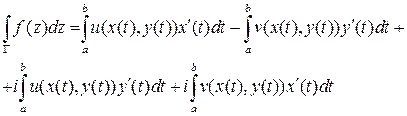
Как обычно, компактная формула векторного анализа при переходе к вычислению превращается в длинное описание. Переход от произвольной функции комплексной переменой в общем случае не меняет ситуации. Однако для замкнутых контуров картина резко меняется.
Чтобы точно описать это утверждение, нужно уточнить терминологию.
Определение. Область комплексной плоскости называется односвязной, если любой замкнутый путь в этой области можно стянуть в точку, не выходя из области.
Пример.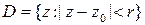 
– открытый круг, 
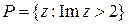-- открытая полуплоскость, множество 
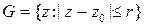не является открытым, так как все точки его границы не обладают требуемым свойством, множество
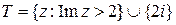не является открытым, так как в точке 
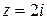не выполнено требуемое свойство. Все перечисленные множества являются односвязными. Область 
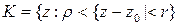(кольцо) не является односвязным, множество 
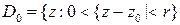(проколотый круг) то же не односвязно.
Теорема Коши. Пусть 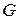– односвязная область 
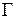– замкнутый контур внутри области. Тогда интеграл от аналитической в области 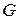функции 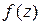контуру 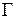равен нулю: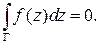 
Доказательство. Условия Коши – Римана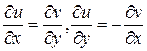 
и формула Грина 
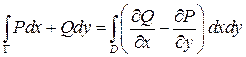гарантируют равенство нулю вещественной и мнимой части интеграла.
Первое важное следствие теоремы Коши – формула, дающая интегрально представление аналитической функции.
Следствие (формула Коши). Если 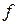аналитическая функция в односвязной области 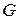, 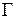– положительно ориентированный замкнутый контур, лежащий в области, и точка 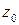находится внутри контура, то справедливо равенство:
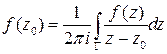
Доказательство. Простое, но очень важное доказательство этой формулы основано, вытекающей из теоремы Коши, независимости интеграла от выбора контура. В формуле Коши подынтегральная функция является аналитической всюду, кроме точки .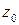
Покажем, что интеграл по контуру 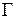равен интегралу по контуру 
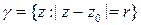-- положительно ориентированной окружности маленького радиуса ( 
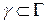). Рассмотрим вспомогательный контур 
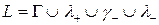, здесь 
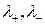дуга соединяющая контуры 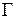и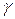 
, пройденная дважды в разных направлениях, 
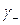контур 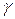, пройденный в отрицательном направлении. При такой компоновке 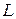окажется замкнутым контуром, внутри которого функция 
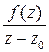аналитична, следовательно 
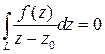. Стандартные свойства криволинейных интегралов второго рода позволяют получить формулу 
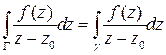. Простые вычисления показывают, что интеграл по контуру 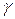стремится к 
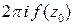при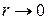 
, с другой стороны все такие интегралы равны интегралу по контуру . Следовательно:
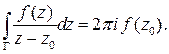
Формула Коши позволяет получить много интересной и полезной информации об аналитических функциях. Первый шаг в этом направлении – формула для производных аналитических функций.
Следствие (формула для производных). Если 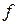аналитическая функция в области 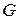, 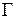– положительно ориентированный замкнутый контур, лежащий в области, и точка 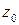находится внутри контура, то функция имеет в этой точке производные всех порядков, причем справедливо равенство:
.
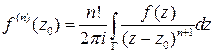Легко дать прямое доказательство этой теоремы, но важно понимать, что формула является следствием теоремы о дифференцировании интеграла по параметру.
Теорема. Если функция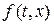 
дифференцируема по 
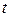и интегралы 
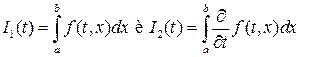сходятся равномерно (т. е. 
,
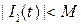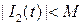), то интеграл можно дифференцировать по параметру
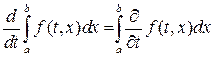
Отметим, что такое поведение совершенно не свойственно неаналитическим функциям одной переменной, которые могут иметь производную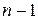 
-го порядка, но не иметь производной 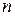-го порядка. Это различие идет и дальше. Функция 
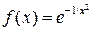может быть непрерывно продолжена в 
, 
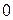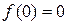, то же справедливо в отношении всех ее производных 
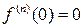. Таким образом мы получаем пример бесконечно дифференцируемой функции, которую нельзя представить в виде ряда Тейлора, но для аналитических функций такое не возможно.
Следствие (ряд Тейлора для аналитической функции). Если 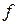аналитическая функция в области 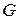, точка 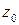находится внутри контура, то в круге 
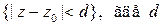расстояние от точки 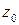до границы области 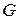, функция допускает разложение в ряд Тейлора:
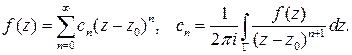
Доказательство. Положим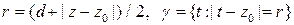 
. Окружность лежит в области 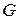, и точка 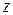лежит внутри окружности. Воспользуемся формулой Коши
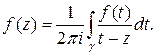
Преобразуем выражение так, что бы дробь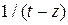 
можно было бы разложить по формуле геометрической прогрессии
,
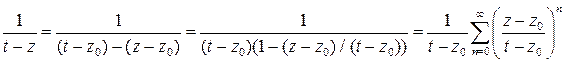здесь мы воспользовались тем, что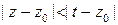 
. Подставим это разложения в интеграл и поменяем местами интеграл и сумму:
.
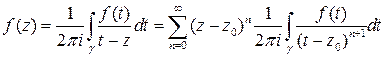Доказанная формула позволяет дать еще одно эквивалентное определение аналитичности: функция является аналитической в области, если она допускает разложение в ряд Тейлора в окрестности любой точки.
Локальные свойства аналитических функций, описные выше, оказывают существенное влияние на поведение функции в целом.
4. Теорема единственности.