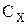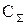Расчет оптимального размера заказа
Наиболее распространенной моделью прикладной теории логистики является модель оптимального или экономичного размера заказа EOQ (Economic Order Quantity). В качестве критерия оптимизации принимается минимум общих затрат 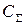 , включающих затраты на выполнение заказов
, включающих затраты на выполнение заказов 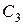 и затраты на хранение запаса на складе
и затраты на хранение запаса на складе 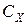 в течение определенного периода (год, квартал и т. п.):
в течение определенного периода (год, квартал и т. п.):
 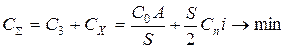
| (5.1) |
где 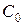 — затраты на выполнение одного заказа, руб.; А — потребность в заказываемом продукте в течение данного периода, шт.;
— затраты на выполнение одного заказа, руб.; А — потребность в заказываемом продукте в течение данного периода, шт.; 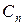 — цена единицы продукции, хранимой на складе, руб.;
— цена единицы продукции, хранимой на складе, руб.; 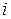 — доля от цены
— доля от цены 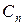 , приходящейся на затраты по хранению;
, приходящейся на затраты по хранению; 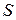 — искомая величина заказа, шт.
— искомая величина заказа, шт.
На рис. 5.1 представлены составляющие затрат 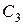 и
и 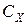 суммарные затраты
суммарные затраты 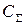 в зависимости от размера заказа.
в зависимости от размера заказа.
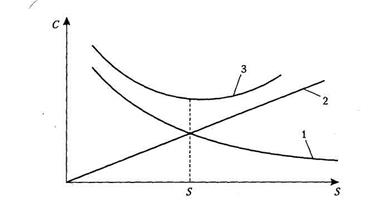
Рис. 5.1. Зависимость затрат от размера заказа: 1 — затраты на выполнение заказа; 2 — затраты на хранение; 3 — суммарные затраты
Из рис. 5.1 видно, что затраты на выполнение заказов с увеличением размера заказа уменьшаются, подчиняясь гиперболической зависимости (кривая 1); затраты на хранение партии поставки возрастают прямо пропорционально размеру заказа (линия 2); кривая общих затрат (кривая 3), имеет вогнутый характер, что говорит о наличии минимума, соответствующего оптимальной партии 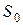 .
.
Значение оптимума 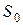 совпадает с точкой пересечения зависимостей
совпадает с точкой пересечения зависимостей 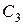 и
и 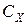 . Это объясняется тем, что абсцисса точки пересечения
. Это объясняется тем, что абсцисса точки пересечения 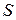 находится из решения уравнения:
находится из решения уравнения:
 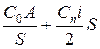
| (5.2) |
т. е.:
 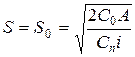
| (5.3) |
При других зависимостях 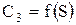 и
и 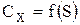 указанного совпадение может не наблюдаться, и в этом случае необходимо применить процедуру оптимизации. Так, для функции (5.1) находим:
указанного совпадение может не наблюдаться, и в этом случае необходимо применить процедуру оптимизации. Так, для функции (5.1) находим:
 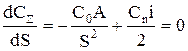
| (5.4) |
Решая уравнение (5.4), приходим к формуле (5.3) для определения EOQ.
Зная 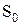 , нетрудно определить:
, нетрудно определить:
• количество заказов:
 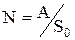
| (5.5) |
минимальные суммарные затраты за рассматриваемый период:
 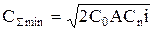
| (5.6) |
время между заказами:
 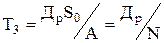
| (5.7) |
где 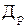 — продолжительность рассматриваемого периода. Если речь идет о количестве рабочих дней в году, то
— продолжительность рассматриваемого периода. Если речь идет о количестве рабочих дней в году, то 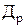 = 260 дн., если о количестве недель, то
= 260 дн., если о количестве недель, то 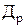 — 52 недели.
— 52 недели.
В модели (5.1) предполагается, что оплата за хранение единицы продукции пропорциональна ее цене, а среднее количество находящейся на хранении продукции при постоянной интенсивности спроса на данный период равно:
 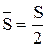
| (5.8) |
Из рис. 5.2 виден принцип получения зависимости 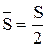 .Так, если бы за время
.Так, если бы за время  был произведен один заказ, равный потребности в заказываемом продукте
был произведен один заказ, равный потребности в заказываемом продукте  , то в среднем на хранении находилось бы
, то в среднем на хранении находилось бы 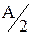 продукции. Если два заказа с интервалом
продукции. Если два заказа с интервалом 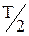 , то среднее количество хранимой продукции было бы
, то среднее количество хранимой продукции было бы 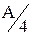 , и т.д.
, и т.д.
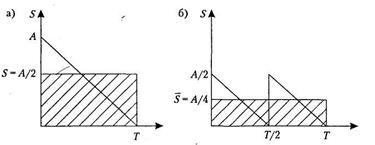
Рис. 5.2. Определение средней величины запаса на складе: а) — максимальный запас А; б) — максимальный запас А/2
Однако практика аренды складских помещений, а также расчеты затрат на хранение на складах ряда фирм говорят о том, что, как правило, учитывается не средний размер партии, а площадь (или объем) склада, которая требуется для всей поступившей партии:
 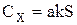
| (5.9) |
где а — затраты на хранение единицы продукции с учетом занимаемой площади (объема) склада, руб./м2 (руб./м3); k — коэффициент, учитывающий пространственные габариты единицы продукции, м2/шт. (м3/шт.).
С учетом (5.9) расчетная формула для оптимальной величины заказа запишется в виде:
 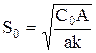
| (5.10) |
Теперь, когда становится ясным, что оплата за хранение продукции может быть связана не только с величиной 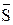 , предлагается ввести более гибкую зависимость вида:
, предлагается ввести более гибкую зависимость вида:
 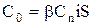
| (5.11) |
где 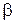 — коэффициент, отражающий связь между долей от стоимости объема заказа и установленной арендной платой. Коэффициент
— коэффициент, отражающий связь между долей от стоимости объема заказа и установленной арендной платой. Коэффициент 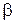 может изменяться в широких пределах.
может изменяться в широких пределах.
При подстановке (5.11) в формулу (5.1) после преобразований находим:
 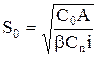
| (5.12) |
При 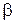 = 0,5 приходим к зависимости (5.3).
= 0,5 приходим к зависимости (5.3).
Вторым не менее важным условием, которое необходимо учитывать при расчете EOQ, являются скидки. Известно, что при покупке партии товара большинство фирм дает скидки, величина которых зависит от размера партии 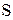 .
.
Аналитическая зависимость общих издержек, связанных с запасами, записывается в виде системы уравнений для каждой j-й цены, и для каждого уравнения рассчитывается оптимальная величина заказа 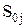 . Если величины
. Если величины 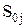 находятся внутри граничных значений j-й партии, то они сохраняются для дальнейших сравнительных расчетов; если нет, то расчеты общих издержек производятся для граничных значений j-й цены и учитываются при сравнении издержек.
находятся внутри граничных значений j-й партии, то они сохраняются для дальнейших сравнительных расчетов; если нет, то расчеты общих издержек производятся для граничных значений j-й цены и учитываются при сравнении издержек.
Таблица 5.1 Изменение цены и затраты на хранение от размера партии
| Номер | Размер партии поставки, ед. | Цена единицы товара 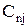 ,у.е. ,у.е.
| Доля от цены на хранение единицы товара 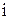
| Затраты на хранение единицы товара 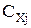 , у.е. , у.е.
|
| 1 | 1-9999 | 2,5 | 0,24 | 0,6 |
| 2 | 10000-19999 | 2,0 | 0,2 | 0,4 |
| 3 | 20000 и более | 1,5 | 0,2 | 0,3 |
Запишем систему уравнений для общих издержек с учетом данных, приведенных в табл. 5.1, и условий, что 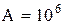 ед.; Со = 2,5 у. е.;
ед.; Со = 2,5 у. е.; 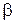 = 0,5:
= 0,5:
 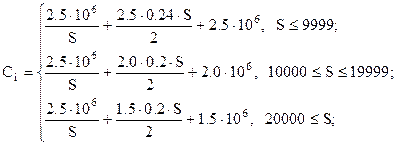
| (5.13) |
С помощью формулы (6.3) находим оптимальные величины заказа для каждой партии: 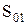 = 9130 ед.;
= 9130 ед.; 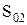 = 11 180 ед.;
= 11 180 ед.; 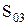 = 12 910 ед.
= 12 910 ед.
Поскольку величины заказов 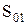 и
и 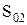 лежат в пределах граничных значений, то они должны быть выбраны в качестве оптимальных. Для третьей величины
лежат в пределах граничных значений, то они должны быть выбраны в качестве оптимальных. Для третьей величины 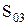 ограничение на размер партии не соблюдается, поэтому рассчитываются минимальные общие издержки на границе при
ограничение на размер партии не соблюдается, поэтому рассчитываются минимальные общие издержки на границе при 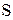 = 20 000 ед.
= 20 000 ед.
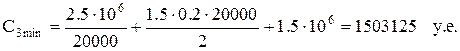
Проведя аналогичные расчеты для второго уравнения при 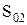 , т. е. для оптимальной партии, находим
, т. е. для оптимальной партии, находим
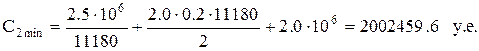
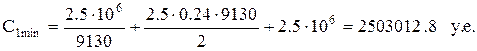
Следовательно, наименьшие общие затраты, связанные с запасами, соответствуют величине партии 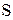 = 20 000 ед.
= 20 000 ед.
При увеличении количества ступеней «лестницы скидок» вместо системы уравнений (5.13) используются непрерывные зависимости (рис. 5.2):
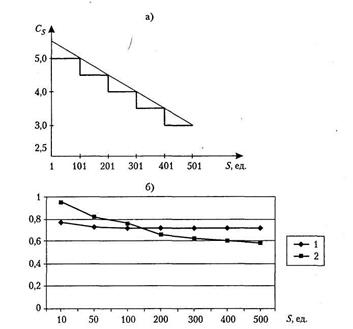
Рис. 5.2. Зависимости, отражающие скидки с цены продукции:
а) - дискретная («ступенчатая») зависимость и ее аппроксимация прямой, формула (5.14);
б) - нелинейные зависимости скидок, формула (5.15): 
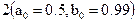
 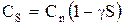
| (5.14) |
или
 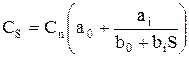
| (5.15) |
где 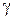 ,
, 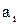 ,
, 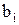 — коэффициенты.
— коэффициенты.
Рассмотрим пример определения 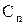 и коэффициента
и коэффициента 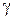 уравнения (5.14) на основании данных, приведенных в табл. 5.3.
уравнения (5.14) на основании данных, приведенных в табл. 5.3.
Таблица 5.3 Скидки с цены за объем закупок.
| Расходы, у.е. | Объем закупок, ед. |
| 5,0 | 1 – 99 |
| 4,5 | 100 – 200 |
| 4,0 | 201 – 300 |
| 3,5 | 301 – 400 |
| 3,0 | 401 - 500 |
Из рис. 5.2 видно, что можно применить разные зависимости: по минимуму, по максимуму или средней величине объема закупок при одинаковой цене за единицу товара. Если выбрана зависимость для максимальных значений, то в качестве опорных точек могут быть взяты любые значения из правого столбца таблицы, например 99 и 300 ед. Тогда уравнения для определения 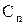 и
и 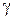 запишутся в виде:
запишутся в виде: 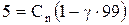
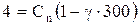
После преобразований и решения системы уравнений, находим 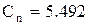 ,
, 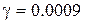 , т. е.
, т. е. 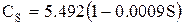 ,
, 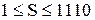 .
.
Рассмотрим зависимость (5.15), рис. 5.2 (б). Коэффициент 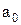 отражает предельное снижение цены единицы продукции
отражает предельное снижение цены единицы продукции 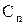 при
при 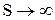 . Допустим, что коэффициент
. Допустим, что коэффициент 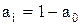 .
.
Коэффициенты 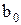 и
и 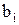 позволяют охарактеризовать изменения кривой
позволяют охарактеризовать изменения кривой 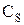 . Предположим, что 0<b0<bi и коэффициенты
. Предположим, что 0<b0<bi и коэффициенты 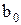 и
и 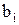 связаны, соотношением
связаны, соотношением 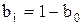 .
.
В табл. 5.4 приведены значения функции 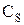 при
при 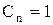 для различных величин заказа
для различных величин заказа 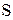 (от 10 до 500), при
(от 10 до 500), при 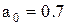 и
и 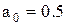 , а также при различных коэффициентах
, а также при различных коэффициентах 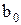 .
.
Таблица 5.4.Изменение величины скидки в зависимости от объема заказа (формула (5.15)
| Заказ S, шт | Коэффициенты b0(при а0=0,7) | Коэффициенты b0(при а0=0,5) | ||||
| 0,7 | 0,9 | 0,99 | 0,7 | 0,9 | 0,99 | |
| 10 | 0,780 | 0,860 | 0,975 | 0,635 | 0,751 | 0,959 |
| 50 | 0,719 | 0,751 | 0,901 | 0,532 | 0,584 | 0,836 |
| 100 | 0,71 | 0,728 | 0,850 | 0,516 | 0,546 | 0,751 |
| 200 | 0,705 | 0,714 | 0,800 | 0,508 | 0,524 | 0,667 |
| 300 | 0,703 | 0,710 | 0,775 | 0,505 | 0,516 | 0,625 |
| 400 | 0,702 | 0,707 | 0,760 | 0,504 | 0,512 | 0,600 |
| 500 | 0,702 | 0,705 | 0,750 | 0,503 | 0,509 | 0,583 |
Из анализа данных табл. 5.4 следует, что функция (5.15) позволяет довольно гибко учитывать зависимость между величиной скидки и объемом заказа.
Для примера рассчитаем коэффициенты 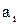 и
и 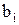 по данным табл. 5.3.
по данным табл. 5.3.
Поскольку предельное уменьшение цены Cmin = 3 у.е., то 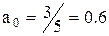 и соответственно
и соответственно 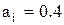 .
.
Для определения коэффициента 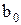 воспользуемся значениями
воспользуемся значениями 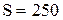 ед., Cs = 4,0 у.е. и после подстановки в уравнение (6.15) получим:
ед., Cs = 4,0 у.е. и после подстановки в уравнение (6.15) получим:
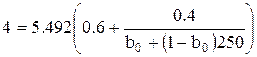
откуда 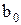 = 0,996,
= 0,996, 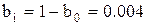 .
.
Определим оптимальный размер заказа с учетом скидки по формуле (6.14) и введения коэффициента р при учете оплаты за хранение. Тогда критериальное уравнение запишется в виде:
 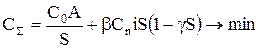
| (5.16) |
Приравняв частную производную 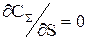 , после преобразований находим:
, после преобразований находим:
 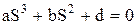
| (5.17) |
где 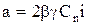 ;
; 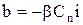 ;
; 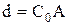 .
.
Для решения кубического уравнения (5.17) можно воспользоваться аналитическим или численным (итерационным) способом.
Аналитический способ. Один из вариантов сводится к следующему:
Вводится новая переменная 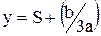 .
.
При подстановке в уравнение (5.17) после преобразований получим:
 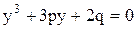
| (5.18) |
Где 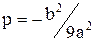 ;
; 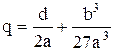
3. Число действительных корней уравнения (6.18) зависит от знака дискриминанта: 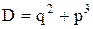
При D > 0 действительный корень равен (формула Кардана):
 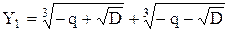
| (5.19) |
При D < 0 для определения корней уравнения (5.18) используются специальные формулы.
Приближенный способ (метод итераций).
Запишем уравнение (5.17) в виде:
 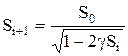
| (5.20) |
где 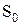 рассчитывается по формуле (5.12).
рассчитывается по формуле (5.12).
Подставив в правую часть 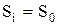 , находим первое приближение
, находим первое приближение 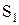 и сравним с
и сравним с 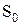 , затем подставляем
, затем подставляем 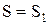 и находим
и находим 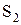 и т. д. Процесс повторяется несколько раз до достижения заданной точности.
и т. д. Процесс повторяется несколько раз до достижения заданной точности.
Пример.
Определим оптимальную величину заказа при учете скидок, формула (5.14), и следующих исходных данных: А = 1200 ед., 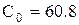 у. е.;
у. е.; 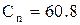 у. е.,
у. е., 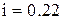 ;
; 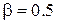 и
и 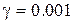 . Тогда уравнение суммарных затрат запишется в виде:
. Тогда уравнение суммарных затрат запишется в виде:
 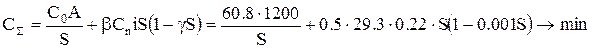
| (5.21) |
Для исследования зависимости 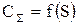 выполним вспомогательные расчеты (табл. 5.5) и построим график
выполним вспомогательные расчеты (табл. 5.5) и построим график 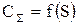 (рис. 5.3).
(рис. 5.3).
При 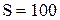 ед., затраты на выполнение заказа составят:
ед., затраты на выполнение заказа составят:
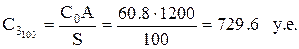 , затраты на хранение без учета скидки составят:
, затраты на хранение без учета скидки составят:
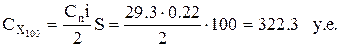 , затраты на хранение с учетом скидки составят
, затраты на хранение с учетом скидки составят
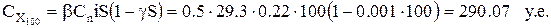
Суммарные затраты 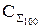 составят:
составят:
без учета скидки: 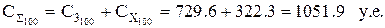
с учетом скидки: 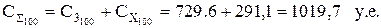
При 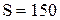 ед., затраты на выполнение заказа составят:
ед., затраты на выполнение заказа составят:
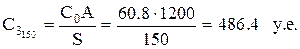 , затраты на хранение без учета скидки составят:
, затраты на хранение без учета скидки составят:
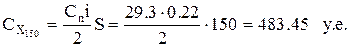 , затраты на хранение с учетом скидки составят
, затраты на хранение с учетом скидки составят
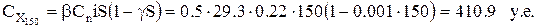
Суммарные затраты 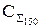 составят:
составят:
без учета скидки: 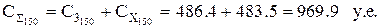
с учетом скидки: 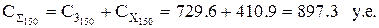
Таблица 5.5 Расчет составляющих и суммарных затрат на выполнение заказа с учетом скидок на величину заказа, формула (5.21)
| Величина заказа, S, ед | Затраты на выполнение заказа | Затраты на хранание, | Суммарные затраты, | ||
| без учета скидки | с учетом скидки | без учета скидки | с учетом скидки | ||
| 100 | 729,6 | 322,3 | 290,1 | 1051,9 | 1019,7 |
| 150 | 486,4 | 483,5 | 410,9 | 969,9 | 897,3 |
| 200 | 364,8 | 644,6 | 515,7 | 1009,4 | 880,5 |
| 250 | 291,8 | 805,5 | 604,3 | 1097,3 | 896,1 |
| 300 | 243,2 | 967,0 | 676,8 | 1210,2 | 919,8 |
| 400 | 182,4 | 1289,2 | 773,3 | 1474,6 | 955,7 |
| 500 | 145,9 | 1611,5 | 805,3 | 1757,4 | 951,1 |
| 600 | 121,6 | 1933,8 | 773,3 | 2055,4 | 895,1 |
| 700 | 104,2 | 2256,1 | 676,8 | 2360,3 | 781,0 |
| 800 | 91,2 | 2578,4 | 515,7 | 2669,6 | 606,9 |
Из рис. 5.3 видно, что учет скидок приводит к изменению традиционной зависимости 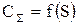 в данном случае у зависимости суммарных затрат
в данном случае у зависимости суммарных затрат 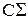 наблюдается не только минимум, но и максимум. Это говорит о том, что если величина заказа ограничена, например S < SА (см. рис. 5.3), то оптимальное значение
наблюдается не только минимум, но и максимум. Это говорит о том, что если величина заказа ограничена, например S < SА (см. рис. 5.3), то оптимальное значение 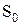 совпадает с минимумом функции
совпадает с минимумом функции 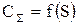 .
.
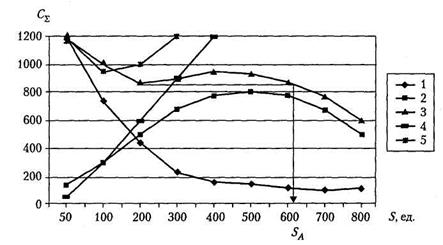
Рис. 5.3. Суммарные затраты на выполнение заказа с учетом скидок на величину заказа, зависимость (5.21): 1 — затраты на выполнение заказа; 2 — затраты на хранение с учетом скидок; 3 — суммарные затраты с учетом скидок; 4 — затраты на хранение (без учета скидок); 5 — суммарные затраты без учета скидок
Для определения 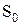 воспользуемся формулой (5.12):
воспользуемся формулой (5.12):
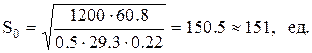
Тогда первое приближение по зависимости (5.20):
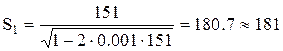
Второе приближение:
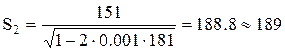
Продолжив вычисления, находим
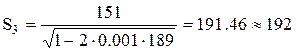
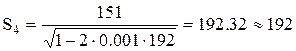
Ввиду того что 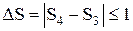 , примем
, примем 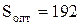 .
.
Исходные данные
| № вар | Величина заказа S, ед. | А,ед. | С0,,у.е. | Сn,,у.е. | i | β | γ | |||||||||
| 1 | 50 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 2700 | 50.1 | 26.4 | 0.12 | 0.6 | 0.001 |
| 2 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 650 | 750 | 800 | 1600 | 51.8 | 21.5 | 0.14 | 0.5 | 0.0009 |
| 3 | 100 | 200 | 250 | 300 | 450 | 550 | 600 | 650 | 750 | 850 | 1700 | 53.1 | 22.2 | 0.19 | 0.4 | 0.0011 |
| 4 | 75 | 150 | 250 | 350 | 500 | 600 | 700 | 800 | 900 | 950 | 3800 | 58.9 | 31.4 | 0.21 | 0.5 | 0.001 |
| 5 | 100 | 125 | 300 | 450 | 500 | 550 | 675 | 750 | 825 | 875 | 3500 | 65.4 | 34.7 | 0.22 | 0.35 | 0.0011 |
| 6 | 100 | 125 | 275 | 350 | 475 | 550 | 625 | 775 | 800 | 850 | 2550 | 60.3 | 33.1 | 0.19 | 0.4 | 0.0008 |
| 7 | 50 | 100 | 150 | 200 | 300 | 500 | 700 | 900 | 1000 | 1100 | 4400 | 59.3 | 31.1 | 0.18 | 0.55 | 0.0007 |
| 8 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 500 | 600 | 2400 | 58.1 | 30.2 | 0.19 | 0.5 | 0.0015 |
| 9 | 100 | 200 | 300 | 350 | 400 | 450 | 500 | 600 | 700 | 800 | 3200 | 59.3 | 35.2 | 0.2 | 0.45 | 0.001 |
| 10 | 200 | 300 | 400 | 500 | 700 | 900 | 1100 | 1300 | 1500 | 1700 | 6800 | 58.4 | 30.1 | 0.17 | 0.3 | 0.0003 |
| 11 | 50 | 100 | 150 | 200 | 300 | 400 | 550 | 700 | 900 | 1000 | 2500 | 45.1 | 27.7 | 0.16 | 0.45 | 0.0005 |
| 12 | 75 | 150 | 300 | 400 | 600 | 800 | 900 | 1000 | 1200 | 1400 | 5600 | 41.2 | 24.1 | 0.2 | 0.6 | 0.0006 |
| 13 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 500 | 600 | 700 | 3500 | 58.4 | 30.1 | 0.16 | 0.45 | 0.0013 |
| 14 | 75 | 150 | 250 | 350 | 500 | 700 | 900 | 1100 | 1200 | 1500 | 3000 | 58.1 | 30.2 | 0.2 | 0.45 | 0.0004 |
| 15 | 100 | 200 | 300 | 450 | 550 | 600 | 650 | 700 | 750 | 850 | 4250 | 59.3 | 31.1 | 0.21 | 0.5 | 0.001 |
| 16 | 50 | 100 | 200 | 300 | 400 | 600 | 800 | 900 | 950 | 1000 | 2000 | 58.4 | 30.1 | 0.19 | 0.4 | 0.0009 |
| 17 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 650 | 750 | 800 | 3200 | 41.2 | 19.1 | 0.21 | 0.5 | 0.001 |
| 18 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 500 | 600 | 1800 | 65.4 | 34.7 | 0.2 | 0.6 | 0.0014 |
| 19 | 100 | 200 | 400 | 450 | 550 | 675 | 750 | 825 | 875 | 950 | 2850 | 58.4 | 30.1 | 0.21 | 0.5 | 0.0008 |
| 20 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 500 | 600 | 700 | 2100 | 58.4 | 30.1 | 0.2 | 0.45 | 0.001 |
| 21 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 700 | 900 | 1200 | 4800 | 59.3 | 31.1 | 0.16 | 0.45 | 0.0003 |
| 22 | 100 | 125 | 250 | 350 | 500 | 650 | 800 | 950 | 1100 | 1250 | 1450 | 58.4 | 30.1 | 0.16 | 0.45 | 0.0004 |
| 23 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 500 | 600 | 1200 | 41.2 | 25.5 | 0.22 | 0.35 | 0.0011 |
| 24 | 50 | 100 | 150 | 200 | 300 | 400 | 550 | 700 | 900 | 1000 | 4000 | 59.3 | 31.1 | 0.21 | 0.5 | 0.0008 |
| 25 | 100 | 200 | 250 | 300 | 450 | 550 | 600 | 650 | 750 | 800 | 2400 | 58.4 | 30.1 | 0.18 | 0.55 | 0.0011 |
Практическое занятие №6