Например, в качестве можно выбрать средние значения или оценки времени выполнения каждой операции с заданной доверительной вероятностью .
Противоречивый характер издержек выполнения операций ФЦ 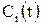 говорит о существовании минимума. Так, например, при транспортировке издержки по доставке возрастают при уменьшении времени доставки, тогда как увеличение времени хранения приводит к увеличению затрат.
говорит о существовании минимума. Так, например, при транспортировке издержки по доставке возрастают при уменьшении времени доставки, тогда как увеличение времени хранения приводит к увеличению затрат.
Если средние значения 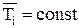 , то измерителем неопределенности ФЦ являются дисперсии
, то измерителем неопределенности ФЦ являются дисперсии 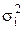 и зависимость (4.4) можно представить, в частности, следующим образом:
и зависимость (4.4) можно представить, в частности, следующим образом:
 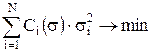
| (4.5) |
где 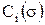 — зависимость издержек выполнения i-й операции ФЦ от рассеивания (неопределенности) времени ее выполнения.
— зависимость издержек выполнения i-й операции ФЦ от рассеивания (неопределенности) времени ее выполнения.
Рассмотрим пример.
Необходимо определить вероятность поставки за 14 дней от момента заказа «точно во время» для ФЦ, связанного с поставкой готовой продукции потребителю. На основании исходных данных взяты максимальные и минимальные сроки выполнения каждой операции, основанные на статистических данных; там же взяты максимальные значения времени, требуемого для завершения каждой операции.
Таблица 5.1 Статистические параметры продолжительности операции ФЦ
| Операция цикла заказа | Размах значений
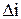 , дни , дни
| Статистика выполнения заказа | Время ТMi соответств. максимуму f(x), дни |
| Передача | 0,5 – 3,0 | 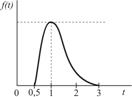
| 1,0 |
| Обработка | 1,0 – 4,0 | 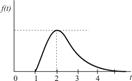
| 2,0 |
| Комплектование | 1,0 – 20,0 | 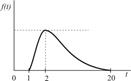
| 2,0 |
| Транспортировка | 2,0 – 10,0 | 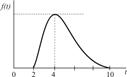
| 4,0 |
| Доставка потребителю | 0,5 – 3,0 | 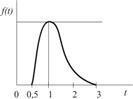
| 1,0 |
| Итого: | 5 - 40 | 10 |
Функциональный цикл включает пять операций: передача заказа, обработка заказа, комплектование заказа, транспортировка, доставка потребителю. Как видим, продолжительность ФЦ колеблется от 5 до 40 дней, а ожидаемая («средняя») продолжительность 10 дней. Считается, что если продолжительность общего цикла больше или меньше Т=10 дней, то это приводит к «излишним затратам ресурсов и снижает общую эффективность логистики».
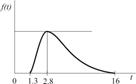
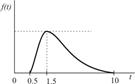
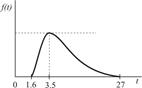
Для расчетов по формуле (4.3) необходимо определить величины ас Из графиков исходных данных видно, что плотности распределения fi(T) асимметричны и отличаются от нормального закона. Ввиду отсутствия достаточной информации допустим, что операции передачи и обработки заказа, а также транспортировки и доставки потребителю подчиняются закону распределения Рэлея:
 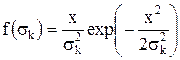
| (4.6) |
где 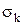 — параметр распределения Рэлея.
— параметр распределения Рэлея.
Известно, что для распределения Рэлея между параметром 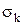 и статистическими параметрами наблюдаются следующие соотношения:
и статистическими параметрами наблюдаются следующие соотношения:
• для математического ожидания (или среднего значения):
 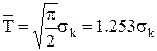
| (4.7) |
• для среднего квадратического отклонения:
 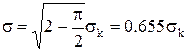
| (4.8) |
• для медианы (серединное или вероятное значение, при котором
функция распределения 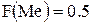 :
:
 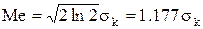
| (4.9) |
• для моды (в случае непрерывного распределения плотности вероятности/(Мо) имеет наибольшее значение):
 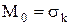
| (4.10) |
Если принять, что максимальное значение плотности распределения 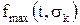 соответствует моде Мо, то искомые значения
соответствует моде Мо, то искомые значения 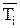 и
и 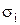 должны рассчитываться по формулам:
должны рассчитываться по формулам:
 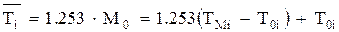
| (4.11) |
 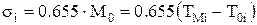
| (4.12) |
где 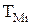 — значение аргумента (продолжительности операции), соответствующее максимуму
— значение аргумента (продолжительности операции), соответствующее максимуму 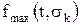 ;
; 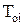 — параметр сдвига.
— параметр сдвига.
Например, для определения 
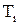 , и
, и 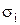 операции передачи заказа по формулам (4.11), (4.12) находим:
операции передачи заказа по формулам (4.11), (4.12) находим:
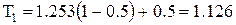 дн.;
дн.;
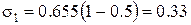 дн.
дн.
- для определения 
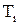 , и
, и 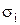 операции обработки заказа по тем же формулам находим:
операции обработки заказа по тем же формулам находим:
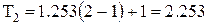 дн.;
дн.;
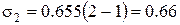 дн.
дн.
И так далее по всем позициям
Результаты расчета 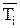 и
и 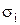 подставим в таблицу (см.табл.4.2)
подставим в таблицу (см.табл.4.2)
Анализ операции «комплектования заказа» показал, что с таким размахом значений (Д = 20-1=19 дн.) и максимальным значением, соответствующим Ттах = 2 дн., плотность распределения представляет собой суперпозицию двух плотностей распределений или композицию двух случайных величин, подчиняющихся различным законам распределения.
Выберем для аппроксимации суперпозицию двух распределений — Рэлея и равномерной плотности, которая записывается в виде:
 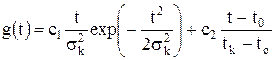
| (4.13) |
где 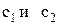 — коэффициенты,
— коэффициенты, 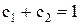 .
.
Для расчета среднего значения и дисперсии суперпозиции распределений g(t) используются формулы:
 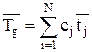
| (4.14) |
 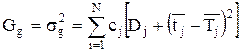
| (4.15) |
где 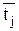 ,
, 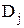 — среднее значение и дисперсия n-го распределения; n — количество распределений, n = 2.
— среднее значение и дисперсия n-го распределения; n — количество распределений, n = 2.
Параметры распределения равномерной плотности для операции «комплектование заказа»определяются по формулам:
 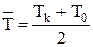
| (4.16) |
 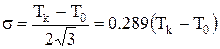
| (4.17) |
При Tk = 20, То=1 получим:
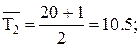
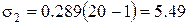
Полученные результаты расчетов заносим в таблицу 4.3
Подставляя значения средних и дисперсий в формулы и принимая значения коэффициентов с1 = 0,9, с2 = 0,1 , находим:
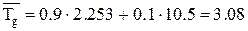
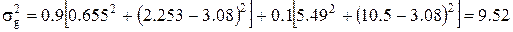
Таблица 4.2. Предварительный расчет продолжительности операций обработки заказа
Таблица 4.3. Расчет продолжительности операций обработки заказа
| Операция цикла заказа | Размах значений, дни | Время ТMi соответств. максимуму f(x), дни | Средние значения | Среднее значение Тi, дни | Среднее квадратич. отклонение, дни. | Вариант измененных, дни | |||
| Распределение Рэлея | Распределение равномерной плотности | ||||||||
| Среднее значение Тi, дни | Среднее квадратич. отклонение, дни. | Среднее значение Тi, дни | Среднее квадратич. отклонение, дни. | ||||||
| Передача | 0,5 – 3,0 | 1,0 | 1,126 | 0,33 | 1,126 | 0,33 | |||
| Обработка | 1,0 – 4,0 | 2,0 | 2,253 | 0,665 | 2,253 | 0,665 | |||
| Комплектование | 1,0 – 20,0 | 2,0 | 2,253 | 0,665 | 10,5 | 5,49 | 3,08 | 3,09 | |
| Транспортировка | 2,0 – 10,0 | 4,0 | 4,506 | 1,131 | 4,506 | 1,131 | |||
| Доставка потребителю | 0,5 – 3,0 | 1,0 | 1,126 | 0,33 | 1,126 | 0,33 | |||
| Итого: | 5 - 40 | 10 | |||||||
| Операция цикла заказа | Размах значений, дни | Время ТMi соответств. максимуму f(x), дни | Средние значения | Среднее значение Тi, дни | Среднее квадратич. отклонение, дни. | Вариант измененных, дни | |||
| Распределение Рэлея | Распределение равномерной плотности | ||||||||
| Среднее значение Тi, дни | Среднее квадратич. отклонение, дни. | Среднее значение Тi, дни | Среднее квадратич. отклонение, дни. | ||||||
| Передача | 0,5 – 3,0 | 1,0 | 1,126 | 0,33 | |||||
| Обработка | 1,0 – 4,0 | 2,0 | 2,253 | 0,665 | |||||
| Комплектование | 1,0 – 20,0 | 2,0 | 2,253 | 0,665 | |||||
| Транспортировка | 2,0 – 10,0 | 4,0 | 4,506 | 1,131 | |||||
| Доставка потребителю | 0,5 – 3,0 | 1,0 | 1,126 | 0,33 | |||||
| Итого: | 5 - 40 | 10 | |||||||
Таким образом, для операции «комплектования заказа» среднее значение 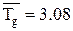 среднее квадратическое отклонение
среднее квадратическое отклонение 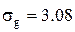 .
.
После того как определены статистические параметры всех операций, определим характеристики для общего цикла выполнения заказа: среднее значение, формула (4.1):
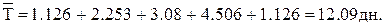
Среднее квадратическое отклонение, формула (4.2) (при условии отсутствия корреляции между операциями ФЦ):
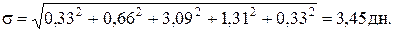
Рассчитаем вероятность выполнения заказа за 14 дней. При подстановке значений в формулу (4.3) находим:
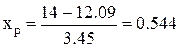
Воспользовавшись табл. 4.4, определим вероятность выполнения заказа.
Таблица 4.4. Значения вероятности Р(х) нормальной функции распределения от параметра X
| X | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
| 0 | .5000 | .5040 | .5080 | .5120 | .5160 | .5199 | .5239 | .5279 | .5319 | .5359 |
| .1 | .5398 | .5438 | .5478 | .5517 | .5557 | .5596 | .5636 | .5675 | .5714 | .5753 |
| .2 | .5793 | .5832 | .5871 | .5910 | .5948 | .5987 | .6026 | .6064 | .6103 | .6141 |
| .3 | .6179 | .6217 | .6255 | .6293 | .6331 | .6368 | .6406 | .6443 | .6480 | .6517 |
| .4 | .6554 | .6591 | .6628 | .6664 | .6700 | .6736 | .6772 | .6808 | .6844 | .6879 |
| .5 | .6915 | .6950 | .6985 | .7019 | .7054 | .7088 | .7123 | .7157 | .7190 | .7224 |
| .6 | .7257 | .7291 | .7324 | .7357 | .7389 | .7422 | .7454 | .7486 | .7517 | .7549 |
| .7 | .7580 | .7611 | .7642 | .7673 | .7704 | .7734 | .7764 | .7794 | .7823 | .7852 |
| .8 | .7881 | .7910 | .7939 | .7967 | .7995 | .8023 | .8051 | .8078 | .8106 | .8133 |
| .9 | .8159 | .8186 | .8212 | .8238 | .8264 | .8289 | .8315 | .8340 | .8365 | .8389 |
| 1.0 | .8413 | .8438 | .8461 | .8485 | .8508 | .8531 | .8554 | .8577 | .8599 | .8621 |
| 1.1 | .8643 | .8665 | .8686 | .8708 | .8729 | .8749 | .8770 | .8790 | .8810 | .8830 |
| 1.2 | .8849 | .8869 | .8888 | .8907 | .8925 | .8944 | .8962 | .8980 | .8997 | .9015 |
| 1.3 | .9032 | .9049 | .9066 | .9082 | .9099 | .9115 | .9131 | .9147 | .9162 | .9177 |
| 1.4 | .9192 | .9207 | .9222 | .9236 | .9251 | .9265 | .9279 | .9292 | .9306 | .9319 |
| 1.5 | .9332 | .9345 | .9357 | .9370 | .9382 | .9394 | .9406 | .9418 | .9429 | .9441 |
| 1.6 | .9452 | .9463 | .9474 | .9484 | .9495 | .9505 | .9515 | .9525 | .9535 | .9545 |
| 1.7 | .9554 | .9564 | .9573 | .9582 | .9591 | .9599 | .9608 | .9616 | .9625 | .9633 |
| 1.8 | .9641 | .9649 | .9656 | .9664 | .9671 | .9678 | .9686 | .9693 | .9699 | .9706 |
| 1.9 | .9713 | .9719 | .9726 | .9732 | .9738 | .9744 | .9750 | .9756 | .9761 | .9767 |
| 2.0 | .9772 | .9778 | .9783 | .9788 | .9793 | .9798 | .9803 | .9808 | .9812 | .9817 |
| 2.1 | .9821 | .9826 | .9830 | .9834 | .9838 | .9842 | .9846 | .9850 | .9854 | .9857 |
| 2.2 | .9861 | .9864 | .9868 | .9871 | .9875 | .9878 | .9881 | .9884 | .9887 | .9890 |
| 2.3 | .9893 | .9896 | .9898 | .9901 | .9904 | .9906 | .9909 | .9911 | .9913 | .9916 |
| 2.4 | .9918 | .9920 | .9922 | .9925 | .9927 | .9929 | .9931 | .9932 | .9934 | .9936 |
| 2.5 | .9938 | .9940 | .9941 | .9943 | .9945 | .9946 | .9948 | .9949 | .9951 | .9952 |
| 2.6 | .9953 | .9955 | .9956 | .9957 | .9959 | .9960 | .9961 | .9962 | .9963 | .9964 |
| 2.7 | .9965 | .9966 | .9967 | .9968 | .9969 | .9970 | .9971 | .9972 | .9973 | .9974 |
| 2.8 | .9974 | .9975 | .9976 | .9977 | .9977 | .9978 | .9979 | .9979 | .9980 | .9981 |
| 2.9 | .9981 | .9982 | .9982 | .9983 | .9984 | .9984 | .9985 | .9985 | .9986 | .9986 |
| 3.0 | .9987 | .9987 | .9987 | .9988 | .9988 | .9989 | .9989 | .9989 | .9990 | .9990 |
| 3.1 | .9990 | .9991 | .9991 | .9991 | .9992 | .9992 | .9992 | .9992 | .9993 | .9993 |
| 3.2 | .9993 | .9993 | .9994 | .9994 | .9994 | .9994 | .9994 | .9995 | .9995 | .9995 |
| 3.3 | .9995 | .9995 | .9995 | .9996 | .9996 | .9996 | .9996 | .9996 | .9996 | .9997 |
| 3.4 | .9997 | .9997 | .9997 | .9997 | .9997 | .9997 | .9997 | .9997 | .9997 | .9998 |
В нашем случае 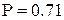 .
.
Это невысокое значение, поскольку возможен срыв около 30% заказов (рекомендуется не более 15%).
Допустим, что в результате проведенных мероприятий удалось уменьшить разброс времени выполнения операций ФЦ, что привело к уменьшению 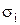 (табл. 4.5).
(табл. 4.5).
Таблица 4.5. Расчет продолжительности операций обработки заказа
| Операция цикла заказа | Размах значений, дни | Время ТMi соответств. максимуму f(x), дни | Среднее значение Тi, дни | Среднее квадратич. отклонение, дни. | Вариант измененных, дни | |
| Передача | 0,5 – 3,0 | 1,0 | 1,126 | 0,33 | 0,2 | |
| Обработка | 1,0 – 4,0 | 2,0 | 2,253 | 0,665 | 0,5 | |
| Комплектование | 1,0 – 20,0 | 2,0 | 3,08 | 3,09 | 1,5 | |
| Транспортировка | 2,0 – 10,0 | 4,0 | 4,506 | 1,131 | 1,0 | |
| Доставка потребителю | 0,5 – 3,0 | 1,0 | 1,126 | 0,33 | 0,2 | |
| Итого: | 5 - 40 | 10 | 12,09 | 3,45 | 1,89 |
В этом случае:
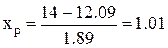
Тогда вероятность доставки продукции «точно вовремя» через 14 дней 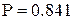 , что в пределах нормы.
, что в пределах нормы.
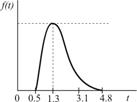
ИСХОДНЫЕ ДАННЫЕ
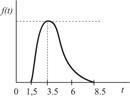
Определить вероятность доставки продукции «точно вовремя» за 21 день для ФЦ, связанного с поставкой готовой продукции потребителю.
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 |
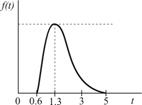
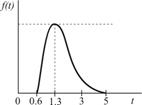
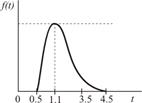
| Передача заказа | 
| 
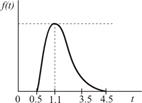
| 
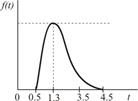
| 
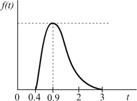
| 
| 
|
| Обработка заказа | 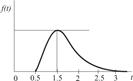
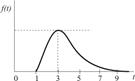
| 
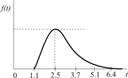
| 
| 
| 
| 
|
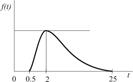
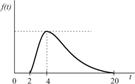
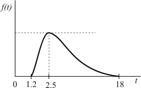
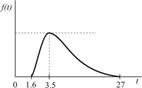
| Комплектование заказа | 
| 
| 
| 
| 
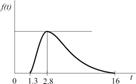
| 
|
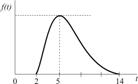
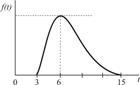
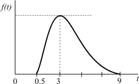
| Транспортировка заказа | 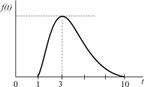
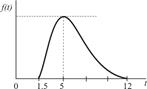
| 
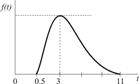
| 
| 
| 
| 
|
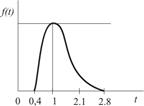
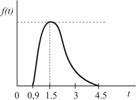
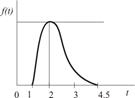
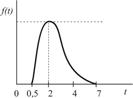
| Доставка заказа потребителю | 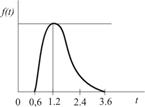
| 
| 
| 
| 
| 
|
| Вариант | 7 | 8 | 9 | 10 | 11 | 12 |
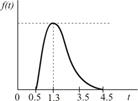
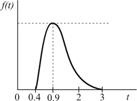
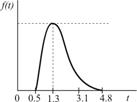
| Передача заказа | 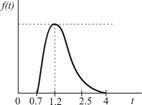
| 
| 
| 
| 
| 
|
| Обработка заказа | 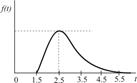
| 
| 
| 
| 
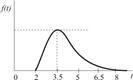
| 
|
| Комплектование заказа | 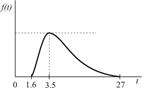
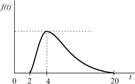
| 
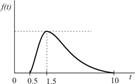
| 
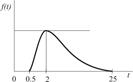
| 
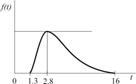
| 
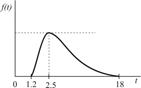
| 
|
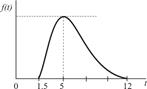
| Транспортировка заказа | 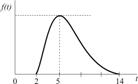
| 
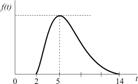
| 
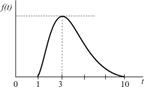
| 
| 
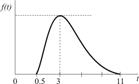
| 
|
| Доставка заказа потребителю | 
| 
| 
| 
| 
| 
|
| Вариант | 13 | 14 | 15 | 16 | 17 | 18 |
| Передача заказа | 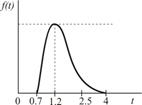
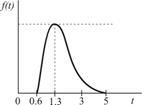
| 
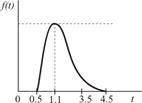
| 
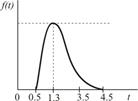
| 
| 
| 
|
| Обработка заказа | 
| 
| 
| 
| 
| 
|
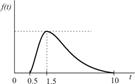
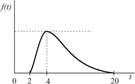
| Комплектование заказа | 
| 
| 
| 
| 
| 
|
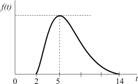
| Транспортировка заказа | 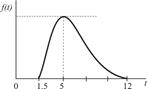
| 
| 
| 
| 
| 
|
| Доставка заказа потребителю | 
| 
| 
| 
| 
| 
|
| Вариант | 19 | 20 | 21 | 22 | 23 | 24 |
| Передача заказа | 
| 
| 
| 
| 
| 
|
| Обработка заказа | 
| 
| 
| 
| 
| 
|
| Комплектование заказа | 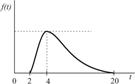
| 
| 
| 
| 
|  . .
|
| Транспортировка заказа | 
| 
| 
| 
| 
| 
|
| Доставка заказа потребителю | 
| 
| 
| 
| 
| 
|
Практическое занятие №5








