Восточноукраинский государственный университет
МИНИСТЕРСТВО ОБРАЗОВАНИЯУКРАИНЫ
ВОСТОЧНОУКРАИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям, курсовому и дипломному проектированию по дисциплине «Логистика тран c портных систем» для студентов, обучающихся по направлению 1004-Транспортные технологии.
"К печати в свет разрешаю"
Проректор по
учебной работе ________________
Протокол N___ от "___"_________ 200__ г.
Составители: А.В.Заверкин
Г.И.Нечаев
Рецензенты: О.И.Иваненко
Весь цифровой и фактический материал,
библиографические сведения проверены.
Написание единиц соответствует стандартам.
Луганск ВНУ 2005
МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ
ВОСТОЧНОУКРАИНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям, курсовому и дипломному проектированию по дисциплине «Логистика транспортных систем» для студентов, обучающихся по направлению 1004-Транспортные технологии.
УТВЕРЖДЕНО
на заседании кафедры транспортных технологий.
Протокол №__ от ____200_
Луганск ВНУ 2005
УДК
Методические указания к практическим занятиям, курсовому и дипломному проектированию по дисциплине «Логистика транспортных систем» для студентов, обучающихся по направлению 1004-Транспортные технологии./ Сост. А.В.Заверкин, Г.И.Нечаев – Луганск: Изд-во Восточноукр.нац.ун-та, 2005. – 55 с.
Методические указания разработаны на основе утвержденной программы учебно-методическим управлением и предназначены для проведения лабораторных работ по дисциплине «Логистика транспортных систем». Может быть использована студентами про курсовом и дипломном проектировании.
| Составители: | А.В.Заверкин, доц. Г.И.Нечаев, проф. |
| Отв. за выпуск | В.А.Закрецкий, доц. |
| Рецензент | О.И.Иваненко, доц. |
Практическое занятие №1
Теория и практика логистического анализа
В основе логистического анализа лежит применение логистической функции, с помощью которой описываются законы роста, присущего многим формам и уровням жизни, а также сфере материального производства и процессам насыщения потребительского спроса. Например, спроса на цветные телевизоры: сначала медленный, но все ускоряющийся рост доли семей, имеющих телевизор, переходящий в равномерный рост; затем рост доли семей, имеющих телевизор, замедляется по мере приближения этого показателя к 100%.
График логистической функции имеет форму латинской буквы «S», положенной на бок. Поэтому его еще называют S-образной кривой. Эта кривая имеет две точки перегиба и характеризуется переходом от ускоряющегося роста к равномерному .(вогнутость) и от равномерного роста к замедляющемуся (выпуклость).
В целом логистический закон отражает динамику многих процессов в пространстве и во времени (например, зарождения нового организма или популяции, их отмирания, различных переходных состояний и т.п.). Логистической закономерности присуще свойство отражать изменения возрастающего ускорения процесса на замедляющееся или, наоборот, - при обратной форме кривой. Эта важная особенность дает возможность определить статистическим путем различные критические, оптимальные и другие практически ценные точки.
В основе логистической функции лежит закономерность, выраженная уравнением Ферхюльста:
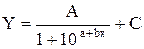
| (1.1) |
где Y-значение функции;
X-время;
А-расстояние между верхней и нижней асимптотами;
С-нижняя асимптота, т. е. предел, с которого начинается • рост функции;
a, b-параметры, определяющие наклон, изгиб и точки перегиба графика логистической функции (рис. 3.1).
Для решения уравнения логистической функции первоначально надо определить верхнюю и нижнюю асимптоты. Это с достаточной точностью можно сделать по эмпирическому ряду путем простого его просмотра. Значение верхней асимптоты можно проверить аналитически по формуле:
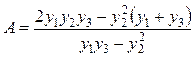
| (1.2) |
где y1, y2, y3 - три эмпирических значения функции, взятые через равные интервалы аргумента.
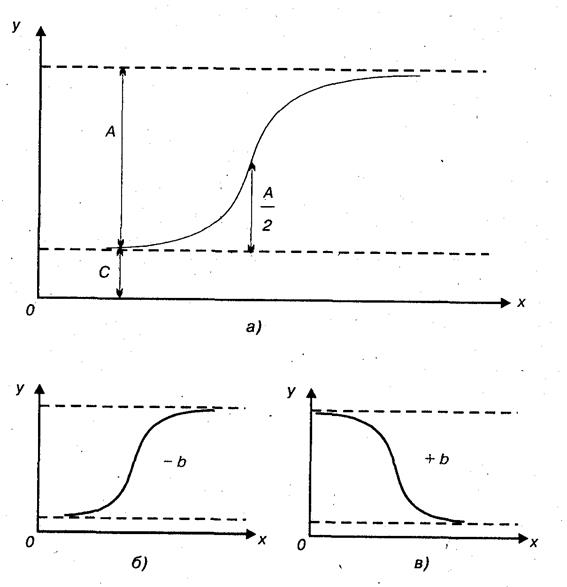 РиРис. 1.1. Графики логистических функций
РиРис. 1.1. Графики логистических функций
Затем уравнение логистической функции выражается в следующей логарифмической форме:
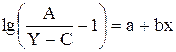
| (1.3) |
Обозначив левую часть этого уравнения через lg Z получим параболу первого порядка:
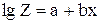
| (1.4) |
Для определения параметров этого уравнения служит следующая система нормальных уравнений, решаемая методом наименьших квадратов:
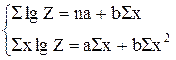
| (1.5) |
Если найти из этих уравнений параметры а и b, то можно составить ряд величин (a+bx), равных теоретическим значениям lg(A/(yx-C)-1). Определяя величины (A/(yx-C)-1), легко составить ряд теоретических значений функции yx. Если С=О, а верхняя асимптота = 100%, или 1, то уравнение логистической функции упрощается до формы:
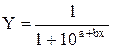
| (1.5) |
Пример логистического анализа
В качестве примера логистического анализа рассмотрим определение логистической закономерности, описывающей конверсию автомобильной промышленности США на производство военной продукции во время второй мировой войны. Главными видами военной техники, выпускаемой автомобильной промышленностью США в период второй мировой войны, являлись: самолеты, авиадвигатели и их части, военные автомашины, танки и агрегаты к ним, судовое оборудование, пушки, боеприпасы и пр. известны следующие данные об объеме производства военной продукции по годам (табл.1.1).
Таблица 1.1
|
Показатель
| Годы | ||||
| 1940 | 1941 | 1942 | 1943 | 1944 | |
| Объем производства военной продукции, млрд. долл. | 0,14 | 0,9 | 4,7' | 8,7 | 9,2 |
Динамика объема производства военной продукции, выпускаемой автомобильной промышленностью США, представлена на рис. 1.2.
На графике можно выделить следующие периоды:
Период О—К. Наращивание выпуска военной продукции в течение 1941 г. обеспечивалось ростом производства «демобилизационной» продукции на военных заводах и было связано с переходом на трехсменную работу при 7-дневной рабочей неделе и с пуском законсервированных заводов-дублеров.
Период К— L . В первую половину 1942 г. рост выпуска продукции автомобильными фирмами определялся главным образом конверсией гражданской промышленности на выпуск военной продукции. В течение второй половины 1942 г. конверсия продолжалась, но определяющую роль играли перестройка гражданской промышленности и новое строительство.
Период L —М. Рост выпуска военной продукции в течение 1943 г. характеризовался перестройкой гражданской промышленности и вводом в строй вновь созданных объектов.
Найдем уравнение этой закономерности, приняв А =10, С=0, п=5. Для составления системы нормальных уравнений предварительно рассчитаем величины ∑х, ∑х2, ∑ lgZ, ∑х lg Z (табл. 1.2).
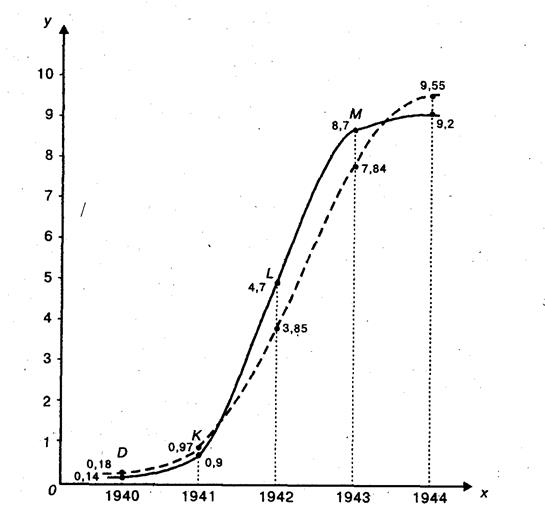
Рис. 1.2. Динамика объема производства военной продукции, выпускаемой автомобильной промышленностью США: по оси абсцисс - время (в годах), по оси ординат - выпуск (в млрд. долл.)
Таблица 1.2 Расчет данных для системы нормальных уравнений
| x | y | x2 | A/Y | (A/Y)-1=Z | lgZ | xlgZ |
| 1 | 0,14 | 1 | 71,42857 | 70,42857 | 1,84775 | 1,84775 |
| 2 | 0,9 | 4 | 11,11111 | 10,11111 | 1,00480 | 2,00960 |
| 3 | 4,7 | 9 | 2,12766 | 1,12766 | 0,05218 | 0,15654 |
| 4 | 8,7 | 16 | 1,14943 | 0,14943 | -0,82556 | -3,30224 |
| 5 | 9,2 | 25 | 1,08696 | 0,08696 | -1,06068 | -5,30340 |
| 15 | — | 55 | — | — | 1,01849 | -4,59175 |
По итогам таблицы составляем систему нормальных уравнений:
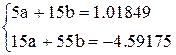
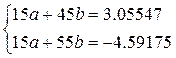
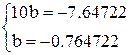
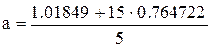
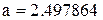
Подставляя в уравнение (1.1) вместо а и b их значения, а также величину А = 10, имеем:
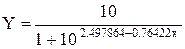
По этому уравнению рассчитываем ожидаемые значения функции 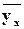 . Расчет показан в табл. 1.3.
. Расчет показан в табл. 1.3.
Таблица 1.3
Расчет значений 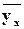
| x | lgZ=a+bx | Z=(A/Y)-1 | Z+1 | (A/Z+1)= 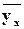
| ( 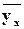 -Y)2 -Y)2
|
| 1 | 1,733142 | 54,09312 | 55,09312 | 0,18 | 0,0016 |
| 2 | 0,96842 | 9,29865 | 10,29865 | 0,97 | 0,0049 |
| 3 | 0,203698 | 1,59845 | 2,59845 | 3,85 | 0,7225 |
| 4 | -0,561024 | 0,274774 | 1,274774 | 7,84 | 0.7396 |
| 5 | -1,325796 | 0,04723 | 1,04723 | 9,55 | 0,1225 |
| ∑1,5911 |
Сравнивая вычисленные значения ( 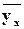 ) с эмпирическими (У), видим, что они достаточно полно согласуются между собой. Более наглядно это представлено на рис. 1.2, где на фоне эмпирической кривой пунктиром изображена и кривая вычисленных значений).
) с эмпирическими (У), видим, что они достаточно полно согласуются между собой. Более наглядно это представлено на рис. 1.2, где на фоне эмпирической кривой пунктиром изображена и кривая вычисленных значений).
Найдем точку перегиба — момент перехода возрастающей скорсти в убывающую:
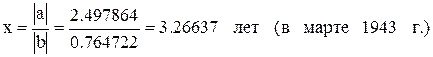
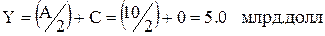
Точка пересечения с осью ординат имеет координаты
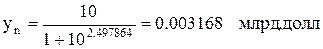
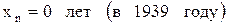
Ошибка составляет
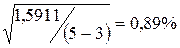
Задания по логистическому анализу
| № вар. | Показатель
| Годы | ||||
| 1990 | 1991 | 1992 | 1993 | 1994 | ||
| 1 | Объем производства продукции | 0,12 | 0,7 | 4,5 | 7,7 | 8,2 |
| 2 | Объем производства продукции | 0,1 | 0,6 | 2,8 | 5,5 | 6,2 |
| 3 | Объем производства продукции | 8,1 | 7,7 | 4,3 | 2,0 | 0,3 |
| 4 | Объем производства продукции | 6,6 | 5,2 | 2,9 | 1,1 | 0,15 |
| 5 | Объем производства продукции | 5,3 | 4,8 | 3,1 | 2,0 | 0,1 |
| 6 | Объем производства продукции | 0,6 | 2,2 | 5,8 | 7,9 | 11,0 |
| 7 | Объем производства продукции | 0,3 | 1,1 | 5,3 | 6,6 | 8,9 |
| 8 | Объем производства продукции | 0,2 | 1,5 | 4,4 | 8,7 | 12,6 |
| 9 | Объем производства продукции | 1,5 | 7,7 | 15,8 | 20,5 | 23,2 |
| 10 | Объем производства продукции | 0,4 | 1,3 | 3,7 | 4,2 | 5,1 |
| 11 | Объем производства продукции | 28,4 | 26,9 | 17,6 | 5,5 | 3,1 |
| 12 | Объем производства продукции | 6,9 | 5,5 | 3,1 | 0,8 | 0,15 |
| 13 | Объем производства продукции | 11,8 | 10,1 | 9,5 | 5,2 | 4,9 |
| 14 | Объем производства продукции | 0,2 | 1,2 | 3,8 | 8,8 | 9,1 |
| 15 | Объем производства продукции | 1,7 | 3,3 | 5,8 | 7,9 | 8,3 |
| 16 | Объем производства продукции | 8,7 | 7,7 | 5,4 | 2,1 | 1,0 |
| 17 | Объем производства продукции | 30,2 | 28,1 | 20,4 | 8,5 | 6,1 |
| 18 | Объем производства продукции | 25,7 | 24,3 | 18,8 | 10,1 | 6,2 |
| 19 | Объем производства продукции | 1,1 | 3,4 | 6,8 | 11,6 | 12,1 |
| 20 | Объем производства продукции | 0,5 | 1,8 | 7,9 | 11,5 | 12,7 |
| 21 | Объем производства продукции | 2,3 | 2,6 | 4,0 | 4,6 | 5,1 |
| 22 | Объем производства продукции | 12,8 | 11,1 | 9,3 | 3,5 | 3,1 |
| 23 | Объем производства продукции | 0,3 | 2,5 | 7,7 | 10,8 | 11,2 |
| 24 | Объем производства продукции | 0,1 | 2,2 | 5,5 | 7,7 | 9,9 |
| 25 | Объем производства продукции | 25,2 | 23,2 | 15,4 | 3,6 | 2,3 |
Провести логистический анализ следующих закономерностей:
1. Процесс насыщения спроса населения на бытовую технику (холодильники, морозильники, телевизоры, компьютеры, автомобили и т.д.).
2. Жизненный цикл отраслей производства вышеназванных видов техники и ряда других (например, паровозов, тепловозов, электровозов, грузовых автомобилей, судов на подводных крыльях, рыболовецких судов, ледоколов, самолетов, вертолетов и т. д.).
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2
МЕТОД АВС.
2.1 ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
В логистике широко используется метод контроля и управления запасами — метод АВС, получивший также названия «правило Парето» и «правило 80/20».
Метод АВС, согласно — «способ формирования и контроля за состоянием запасов, заключающийся в разбиении номенклатуры N реализуемых товарно-материальных ценностей на три неравномощных подмножества A, В и С на основании некоторого формального алгоритма».
Суть данного метода заключается в том, что вся номенклатура материальных ресурсов располагается в порядке убывания суммарной стоимости всех позиций на складе. При этом цену единицы продукции умножают на общее количество и составляют список в порядке убывания произведений. Далее подразделяют все позиции номенклатуры на три группы — А, В и С.
Позиции номенклатуры, отнесенные к группе А, — немногочисленны, но на них приходится преобладающая часть денежных средств, вложенных в запасы. Это особая группа с точки зрения определения величины заказа по каждой позиции номенклатуры, контроля текущего запаса, затрат на доставку и хранение.
К группе В относятся позиции номенклатуры, занимающие среднее положение в формировании запасов склада. По сравнению с позициями номенклатуры группы А они требуют меньшего внимания — производится обычный контроль текущего запаса на складе и своевременности заказа.
Группа С включает позиции номенклатуры, составляющие большую часть запасов: на них приходится незначительная часть финансовых средств, вложенных в запасы. Как правило, по позициям группы С не ведется текущий учет, а проверка наличия осуществляется периодически (один раз в месяц, квартал или полугодие); расчеты оптимальной величины заказа и периода заказа не выполняются.
Для анализа выбираем три метода.
Первый метод, назовем его «эмпирический», базируется на данных обследований. Условно в нем можно выделить несколько вариантов, но наибольший интерес представляет «классический» — «правило Парето», когда координаты точки А принимаются, следующими:  , т.е. «80/20», а координаты точки В соответственно
, т.е. «80/20», а координаты точки В соответственно 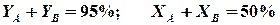 , т.е. «95/50». Таким образом, точка А определяет границу 20% номенклатуры, точка (А+В) — 50% номенклатуры.
, т.е. «95/50». Таким образом, точка А определяет границу 20% номенклатуры, точка (А+В) — 50% номенклатуры.
Второй метод — «дифференциальный» [21].
Последовательность действий следующая:
1) определяются общие затраты по всей номенклатуре 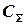
2) рассчитывается средняя стоимость одной позиции номенклатуры 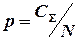 , где N — количество позиций номенклатуры;
, где N — количество позиций номенклатуры;
3) все позиции номенклатуры, затраты на которые в 6 раз и более превышают р, относятся к группе А;
4) все позиции номенклатуры, затраты на которые составляют 0,5р или меньше, относятся к группе С;
5) остальные позиции номенклатуры попадают в группу В.
Несомненное достоинство дифференциального метода — простота;
нет необходимости ранжировать все позиции номенклатуры по стоимости, т. е. располагать в порядке возрастания или убывания, и строить кумулятивную (интегральную или накопленную) зависимость 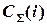 .
.
Третий метод — «аналитический».
Особенность аналитического метода состоит в том, что точки А и В определяются по статистическим данным учета запасов на складе, как в первом методе, но координаты их не строго фиксированы. а зависят от характера зависимости 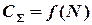 .
.
Суть метода рассмотрим на следующем примере. Допустим, что для всей номенклатуры деталей N известны: 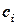 . — стоимость i-й детали,
. — стоимость i-й детали, 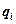 — количество (или оборот) i-й детали на складе в течение рассматриваемого интервала времени.
— количество (или оборот) i-й детали на складе в течение рассматриваемого интервала времени.
Рассчитаем затраты по каждой детали: 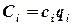 2.1
2.1
Полученные значения 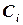 ранжируются — располагаются в убывающей последовательности:
ранжируются — располагаются в убывающей последовательности: 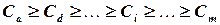 (2.2)
(2.2)
Затем производится присвоение новых индексов: а=1, b=2,..., m=N, где N — общее количество наименований (номенклатура), т. е.:
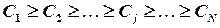 (2.3)
(2.3)
Для удобства расчетов вводятся относительные величины рассматриваемых стоимостных показателей 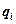 . (в процентах), тем самым производится нормирование показателей:
. (в процентах), тем самым производится нормирование показателей:
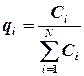 (2.4)
(2.4)
Величины 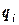 суммируются нарастающим итогом
суммируются нарастающим итогом 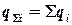 и в зависимости от последующего способа определения номенклатурных групп представляются в виде графика (графический метод) или в случае применения аналитического метода в табличной форме — в виде пар значений (
и в зависимости от последующего способа определения номенклатурных групп представляются в виде графика (графический метод) или в случае применения аналитического метода в табличной форме — в виде пар значений ( 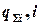 ) для подбора аналитической зависимости:
) для подбора аналитической зависимости:
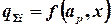 (2.5)
(2.5)
где а — коэффициенты, x— номер детали, x = 1, N.
При графическом способе (рис. 2.1) на оси ординат наносятся значения 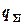 на оси абсцисс — индексы 1, 2, ..i, ... N, соответствующие присвоенным номерам позиций номенклатуры запасных частей. Точки с координатами
на оси абсцисс — индексы 1, 2, ..i, ... N, соответствующие присвоенным номерам позиций номенклатуры запасных частей. Точки с координатами 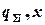 на графике соединяются плавной кривой
на графике соединяются плавной кривой 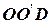 , которая в общем случае является выпуклой. Затем проводится касательная LM к кумулятивной кривой
, которая в общем случае является выпуклой. Затем проводится касательная LM к кумулятивной кривой  , параллельно прямой OD. Прямая OD соответствует равномерному распределению затрат по всей номенклатуре, т. е. характеризует величину показателя осредненной детали:
, параллельно прямой OD. Прямая OD соответствует равномерному распределению затрат по всей номенклатуре, т. е. характеризует величину показателя осредненной детали:
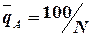 (2.6)
(2.6)
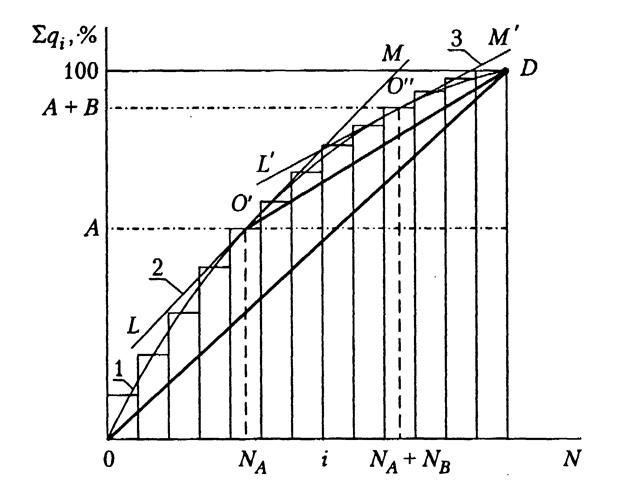
Рис. 3.1. Определение номенклатурных групп АВС: 1 — накопленные затраты по всей номенклатуре деталей; 2 — касательная  к кривой
к кривой 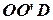 ; 3 — касательная
; 3 — касательная 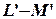 к кривой
к кривой 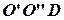
Абсцисса точки касания 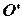 , округленная до ближайшего целого значения отделяет от всей номенклатуры деталей первую группу
, округленная до ближайшего целого значения отделяет от всей номенклатуры деталей первую группу 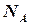 (группа A), в которую входят детали с показателями
(группа A), в которую входят детали с показателями 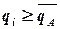 .
.








