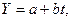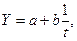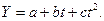Индексный метод в статистических исследованиях
Показатели индексного метода используются в экономических,
ведомственных разработках. В зависимости от характера изучаемого явления
вычисляются индексы объёмных и качественных показателей. Индексы
объемных показателей характеризуют изменение объёма, поступления и
реализации товара, уровня товарных запасов. Индексы качественных
показателей характеризуют изменение цен, издержек обращения,
производительности труда, прибыли, себестоимости, товарооборота. Основой индексного метода является переход от натуральной вещественной формы выражения товарных масс к стоимостным измерителям. Посредством
денежного выражения стоимости отдельных товаров устраняется
несравнимость некоторых показателей и достигается единство.
Б) Построение индексов
Индивидуальные и общие индексы
В зависимсости от степени обобщения единиц изучаемой совокупности, индексы делятся на индивидуальные и общие. Индвивидуальные индексы характеризуют изменения отдельных единиц статистической совокупности (например, по заработной плате, рабочей силе и т.д.). Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц, образующих генеральную совокупность.
Важнейшей особенностью общих индексов являются их свойства.
1.) синтетические;
2) аналитические.
Синтетические свойства состоят в том, что с помощью индексного метода производится агрегирование (соединение) всех разнородных единиц статистической совокупности. Аналитические индексы заключаются в том, что с помощью индексного метода определяется влияние факторов на изменение изучаемого показателя на их взаимодействие, и становится возможным управлять экономическими процессами в нужном направлении. Для определения индекса надо сопоставлять не менее двух величин. При изучении динамики социально-экономических явлений сравниваются величины за текущий (отчётаый) и базисный периоды. Основным элементом индексного отношения является индексируемая величина, т.е. значение признака статистической совокупности, изменение которого является объектом изучения. Индивидуальными индексами являются:
I р =р1/р0, где р1 и ро - цены за единицу товара в текущем и базисном периодах. Iq = q 1 / q 0, где q 1 и q 0 - количество продаж товаров в текущем и базовом периодах.
Результаты расчётов выражаются в коэффициентах или в процентах.
Индивидуальные формы
Общие индексы могуг исчисляться как по агрегатной форме, так и по форме средних, величин (среднеарифметической, средневзвешенной, среднегеометрической, среднегармонической). Выбор формы среднего индекса зависит от характера исходных данных.
В) Агрегатные индексы
Основной формой общего индекса являются агрегатные индексы (от лат. Aggrega-«соединяю»). В числителе и знаменателе общего индекса содержатся наборы (соединения) элементов изучаемого статистического явления. Сопоставимость разнородных единиц достигается введением в индексные отношения специальных сомножителей индексируемых величин-соизмерителей, которые позволяют перейти от натуральных измерений разнородных величин к однородным показателям. В числителе и знаменателе общих индексов изменяются лишь значения индексируемых величин, а их соизмерители = постоянные величины, которые фиксируются на одном (текущем, базисном) уровне. В качестве измерителя индексируемых величин выступают экономические цоказатели.
Разновеликие изменения индивидуальных индексов обуславливают необходимое при их обобщении определения общего индекса для данного изменения цен и количества реализованной продукции. Для этого вычисляют соответственные общие индексы в агрегатной форме.
Аграгатная форма индекса цен предложена немецким экономистом Пааше.
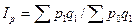 - сумма стоимости продаж в текущем периоде по текущим ценам.
- сумма стоимости продаж в текущем периоде по текущим ценам.
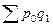 - сумма стоимости продаж товара текущего периода по ценам базисного периода.
- сумма стоимости продаж товара текущего периода по ценам базисного периода.
Сойзмёрители здесь - цены р1 и р0.
При сравнении числителя и знаменателя в разности (абсолютное изменение) определяется показатель абсолютного прироста товарооборота за счёт фактора изменения цен в текущем периоде р1.
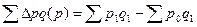 .
.
При другом способе определения агрегатного индекса I в качестве соизмерителя индексируемых величин р1 и р0 могут применяться данные о количестве реализуемых товаров в базисном периоде q 0. Такой индекс называется индексом Ласперейса.
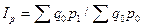 .
.
Показатель прироста товарооборота в базисном и текущем периодах определяется следующим образом:
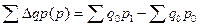 .
.
Таким образом, расчёты, выполненные по формулам Пааше и Ласперейса, имеют разные показания индекса цен. Это объясняется тем, что индкесы Пааше и Ласперейса показывают разные качественные изменения цен. Индекс Пааше характеризует влияние изменения цен на стоимость товаров в отчётном периоде. А индекс Ласперейса показывает влияние изменения цен на стоимость количества товаров, реализуемых в базисном периоде. Другими словами, применение индексов Пааше и Ласперейса зависит от поставленной задачи. При синтезировании общего индекса цен вместо фактического количества товаров в отчётный или базисный периоды в качестве соизмерителей применяются средние величины реализации товаров за два или более периодов. Такой индекс носит название индекса Лоу:
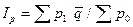 , где
, где
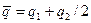 или по взвешенной формуле
или по взвешенной формуле 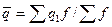
Индекс цен Лоу применяется в расчётах при закупках и реализации товара в течение очень продолжительного периода времени (5-10 лет и т.д.). Этот метод даёт анализ цен с учётом изменений ассортимента товара в суперпериодах.
Большое значение имеет определение цен по ограниченному кругу, т.е. определение наиболее важных товаров, составляющих потребительскую корзину. Рассматриваемая методика определения цен с помощью индексов Паше, Ласперейса, Лоу может применяться в агрегатной форме и к другим индексам качественных показателей. К другим важным видам общих индексов относится индекс, показывающий изменение физического объёма товарной массы.
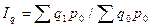
При определении агрегатного индекса физического объём в качестве соизмерителя индексируемых величин q 1 и q 0 выступают цены базисного периода q 0 . В числителе - сумма стоимости товарной массы текущего периода в ценах базисного. А знаменатель - сумма стоимости товарной массы в базисных ценах базисного периода.
При сравнении (разности) товарооборотом, получаем показатель, характеризующий сумму прироста товарооборота в текущем периоде по сравнению с базисным товарооборотом в сопоставимых базисных ценах.
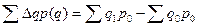 .
.
Агрегатный индекс изменения физического объема товарооборота определяется при использовании соизмерителей q 1 и q0 цен текущего периода.
При определении агрегатных индексов изменения физического объёма товарной массы получаются разные значения, обусловленные применением различных весов-соизмерителей. При индексном анализе коммерческой деятельности следует учитывать, что факторы, влияющие на объём товарооборота, действуют одновременно. Тождественность расчёта прироста товарооборота по вышеперечисленным формулам возможна лишь при применении особой системы весов соизмерителей.
Индекс плановой реализации:
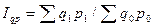 .
.
Определение агрегатных индексов используется при контроле за исполнением плановых заданий. Для определения уровня выполнения плана сопоставляется сумма фактической продажи товарной массы в отчётном периоде и величина планового задания в тех же сопоставимых ценах.
Индекс плановой реализации:
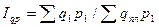 .
.
Существует связь индексов:
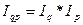 .
.
Значение индекса Iq план: на его основе выявляется влияние отдельных факторов Ip и Iq на изменение товарооборота.
7. Выборочный метод в статистических исследованиях
А) Роль выборки
Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных - результатов наблюдений.
Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результата наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей иследования.
Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование эксперимента), в ходе исследования (последовательный анализ) и решает многие другие задачи. Современную математическую статистику определяют как науку о принятии решений в условиях неопределённости.
Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты.
Иногда проводят сплошное обследование, то есть обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяют сравнительно редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают его изучению.
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
Для того, что бы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если её осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку.
Б) Распределение выборочной совокупности.
Пусть из генеральной совокупности извлечена выборка, причём x 1 наблюдалось n 1 раз, x 2 - n 2 раз, х k - nk раз и 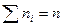 - объём выборки. Наблюдаемые значения х i называют вариантами, а последовательность вариант, записанных в возрастающем порядке, - вариационным рядом. Числа
- объём выборки. Наблюдаемые значения х i называют вариантами, а последовательность вариант, записанных в возрастающем порядке, - вариационным рядом. Числа
наблюдений называют частотами, а их отношения к объёму выборки 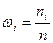 относительными частотами.
относительными частотами.
Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое
распределение можно задать также в виде последовательности интервалов и
соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).
В) Оптимальная численность выборки .
Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N=1000, а объём выборки n=100.
8. Проверка гипотез
А) Проверка гипотез и нулевая гипотеза
Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определённый вид (назовём его А), выдвигают гипотезу: генеральная совокупность распределена по закону А. Таким образом, в этой гипотезе идёт речь о виде предполагаемого распределения.
Возможен случай, когда закон распределения известен, а неизвестны его параметры. Если есть основания предположить, что неизвестный параметр х равен определенному значению х0, выдвигают гипотезу: х=х0. Таким образом, в этой гипотезе речь идёт о предполагаемой величине параметра одного известного распределения.
Возможны и другие гипотезы: о равенстве параметров двух или нескольких распределений, о независимости выборок и др.
Статистической называют гипотезу о виде неизвестного распределения, или о параметрах известных распределений.
Например, статистическими являются гипотезы:
1) Генеральная совокупность распределена по закону Пуассона;
2) Дисперсии двух нормальных совокупностей равны между собой.
Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать.
Нулевой (основной) гипотезой называют выдвинутую гипотезу Н0.
Конкурирующей (альтернативной) называют гипотезу Н1 которая противоречит нулевой.
Различают гипотезы, которые содержат только одно и более одного предположений.
Простой называют гипотезу, содержащую только одно предположение.
Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.
Б) Уровень значимости. Ошибки проверки гипотезы
Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость её проверки. Поскольку проверку производят статистическими методами, её называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, то есть могут быть допущены ошибки двух родов,
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Хочется подчеркнуть, что последствия этих ошибок могут оказаться разными. Например, если отвергнуто правильное решение “продолжать строительство жилого дома”, то эта ошибка первого рода повлечет материальный ущерб; если же принято неправильное решение “продолжать строительство”, несмотря на опасность обвала стройки, то эта ошибка второго рода может повлечь гибель людей.
Вероятность совершить ошибку первого рода принято обозначать α; её называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если, например, принят уровень значимости, равный 0,05, то это означает, что в пяти случаях из ста имеется риск допустить ошибку первого рода (отвергнуть правильную гипотезу).
В) Использование t -распределения Стьюдента
Распределение Стъюдента – это частный случай нормального распределения. Пусть количественный признак X генеральной совокупности распределён нормально, причём среднее квадратическое отклонение неизвестно. Оказывается, что по данным выборки можно построить случайную величину (её возможные значения будем обозначать через t)
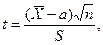
которая имеет распределение, которое называют t-распределением или распределением Стьюдента (псевдоним английского статистика Госсета), с k = n –1 степенями свободы.
Здесь 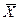 – выборочная средняя,
– выборочная средняя,
S – «исправленное» среднее квадратическое отклонение,
n – объём выборки.
Распределение Стьюдента определяется параметром n – объёмом выборки (или, что то же, числом степеней свободы k = n –1) и не зависит от неизвестных параметров а и s ; эта особенность является его большим достоинством.
Замечание. При неограниченном возрастании объёма выборки n распределение Стьюдента стремится к нормальному. Поэтому практически при n > 30 можно вместо распределения Стьюдента пользоваться нормальным распределением.
Однако важно подчеркнуть, что для малых выборок (n < 30), в особенности для малых значений n, замена распределения нормальным приводит к грубым ошибкам (к повышению точности оценки). Это обстоятельство, вовсе не свидетельствует о слабости метода Стьюдента, а объясняется тем, что малая выборка, разумеется содержит малую информацию об интересующем нас признаке.
9. Тренд-анализ
А) Анализ временных рядов
Ряд данных, взятых в определённый период t и представленных в табличной форме, называют временными рядами. Наиболее важной компонентой временных рядов является тенденция. В экономической литературе линию тенденции называют трендом (от англ. trend).
Данные временных рядов часто изображаются графически. Среди графических изображений временных рядов главными являются:
Тенденция Т,
 Циклическая С,
Циклическая С,
Сезонная S,
Нерегулярная I.
Покажем это на графике:
По оси Y откладываются уровни рядов, по оси Х – года. Главный вектор – это тенденция Т, основные перегибы – циклическая С, внутри которых могут быть зигзаги. Вектор Т показывает главное направление – вверх или вниз. В качестве I выступают времена года, сутки, месяцы, квартал. А по оси Y откладываются уровни временных рядов, количественная оценка или мера развития во времени.
Б) Компоненты временного ряда.
Тенденция является долгосрочной компонентой и определяет общее изменение временного ряда. Прямая, представляющая линию развития во времени, обозначается символом Т.
Сезонная S относится к типу изменения, регулярно повторяющемся во времени. Например, прогноз по рабочей силе, сбыту товара.
Цикличная С – компонента, повторяющаяся волнообразно, длящаяся во времени, но менее короткая, чем Т. Например, деловой цикл – самый важный пример циклической компоненты.
I – нерегулярная компонента, представляющая быстрые изменения малой длительности. Например, ежедневное или еженедельное колебание уровня продаж уравнений в зависимости от погоды.
По классической модели любая заданная величина Y может быть представлена во временном ряду или суммой компонент
Y =Т+С+ S + I .
при условии, что, если рассматривать тенденцию, остальные компоненты «замораживаются».
Заданную величину Y можно представить и произведением воздействующих компонентов.
Y = T · C · S · I .
В) Анализ тенденции Т и сезонной S
Важным направлением социально-экономических исследований является изучение основной тенденции развития (тренда). На практике наиболее распространёнными методами исследований являются:
1) укрупнение интервалов;
2) сглаживание скользящей средней;
3) аналитическое выравнивание.
1.Укрупнение интервалов.
В этом методе главное – это преобразование первоначальных рядов динамики в ряды более продолжительных периодов. Например, преобразование по уровню – это преобразование месячных данных в квартальные, квартальных – в годовые и т.д.
2.Укрупнение интервалов.
В основу этого метода положено определение по эмпирическим данным теоретических уровней, в которых случайные колебания погашаются, а основная линия развития выражается в виде плавной кривой. По новому графику можно определить куда идёт развитие.
| t | Y | |
| 1 | 200 | |
| 2 | 250 | 250 |
| 3 | 300 | 223,3 |
| 4 | 120 | 186,7 |
| 5 | 140 | 150 |
| 6 | 190 | 176,7 |
| 7 | 200 | 170 |
| 8 | 120 |
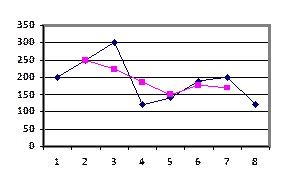
Применение в тренд-анализе рядов динамики метода укрупнения интервалов и метода сглаживания скользящей кривой позволяет выявить тренд для его описания (развития), но не измерение тренда. Измерение тренда можно получить методом аналитического выравнивания, когда основная тенденция развития у t рассматривается как функция времени у = f(t). Определение выровненной функции развития 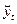 происходит на основе адекватной математической функции, которая наилучшим образом отображает основную тенденцию развития. Подбор адекватных функций осуществляется методом наименьших квадратов. Рассматривается минимум суммы квадратов отклонений, и выравнивание происходит на основе нахождения теоретических кривых (в уравнениях которых появляется новый фактор – время):
происходит на основе адекватной математической функции, которая наилучшим образом отображает основную тенденцию развития. Подбор адекватных функций осуществляется методом наименьших квадратов. Рассматривается минимум суммы квадратов отклонений, и выравнивание происходит на основе нахождения теоретических кривых (в уравнениях которых появляется новый фактор – время):