Взвешенная средняя арифметическая.
До сих пор при определении средней арифметической были те признаки, средние значения которых мы находили. Частоты f показали, сколько раз встречается тот или иной признак. Но не всегда можно найти среднюю арифметическую, базируясь на один признак элементов статистической совокупности, в ряде случаев надо привлекать еще один признак. Например, при продаже хлеба, кроме цены, выписанной из прейскуранта цен, который является не результатом наблюдений, появляется количественный признак -различное распределение веса того или иного сорта. Формула средней арифметической ряда распределения отличается от формулы средней арифметической взвешенной тем, что вместо частот f появляются веса w.
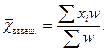
Алгоритм нахождения взвешенной средней арифметической:
1) Устанавливаются правильные веса,
2) Находится произведение xiw
3) Подсчитывается сумма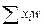 
,
4) Определяется сумма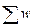 
,
5) Находится взвешенная средняя арифметическая.
Взвешенная средняя арифметическая аналогична центру тяжести в механике, т.е. той точке, в которой происходит равновесие сил. Для итогов взвешивания важны не абсолютные величины, а их соотношения.
Средняя гармоническая вычисляется, когда мы имеем дело с обратными величинами, то есть когда возникает необходимость вычислить среднюю из величин, обратно пропорциональных изучаемому явлению. Например:
1) Отношение производительности к трудоёмкости даёт нам среднюю трудоёмкость.
2) Отношение износа фондов к сроку службы фондов показывает среднее значение срока службы фондов.
3) Отношение уровня рождаемости к общему числу людей даёт среднее число людей, приходящихся на одного рождаемого.
Формула средней гармонической:
1) Простая: 2) Взвешенная:
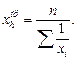
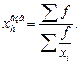
где f – частота,
х i – изучаемый признак.
Средняя геометрическая – применяется при вычислении средних темпов роста.
1) Простая:
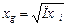
где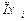 
– произведения признаков.
2) Взвешенная:
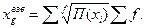
х g всегда меньше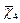 
.
Расстояние между модой и средней арифметической показывает размер пути, который надо пройти основной массе коллектива. Это и будет прогрессивное усвоение опыта передовиков производства, то есть средняя прогрессивная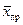 
.
Медиана графическая – это точка на оси абсцисс, в которой площадь графика делится на две равные части.
Мода графическая – это абсцисса точки максимума кривой распределения. Для дискретных рядов – это значение признака, который чаще всего встречается. Для интервальных рядов – это значение признака, который характеризует максимальную плотность распределения.
В) Характеристики вариации.
а) Размах вариации.
Размах вариации является простейшей характеристикой рассеяния вариационного ряда. Размахом вариации R называют разность между наибольшей и наименьшей вариантами:
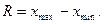
б) Стандарт отклонений.
Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии.
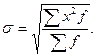
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения. То есть выборочная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.
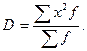
в) Коэффициент вариации.
Коэффициент вариации служит для сравнения величин рассеяния по отношению к выборочной средней двух вариационных рядов: тот из рядов имеет большее рассеяние по отношению к выборочной средней, у которого коэффициент вариации больше. Коэффициент вариации – безразмерная величина, поэтому он пригоден для сравнения рассеяния вариационных рядов, варианты которых имеют различную размерность, например, если варианты одного ряда выражены в сантиметрах, а другого – в граммах.
Коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней.
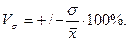
г) Измерение асимметрии, эксцесса.
Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:
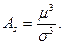
Асимметрия положительна, если «хвост» кривой распределения находится: справа; асимметрия отрицательна, если «хвост» кривой распределения располагается слева.
Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума): если «длинная часть» кривой расположена правее моды, то асимметрия положительна, если слева – отрицательна.
Для оценки крутости, то есть большего или меньшего подъема кривой теоретического распределения по сравнению с нормальной кривой, пользуются характеристикой – эксцессом.
Эксцессом теоретического распределения называют характеристику, которая определяется равенством:
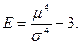
Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и острую вершину, чем нормальная кривая. Если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и плоскую вершину, чем нормальная кривая.
д). Расчёт моментов.
Статистика – это наука о распределении. Показатели вариации: мода, медиана, среднеквадратическое отклонение не дают достаточной информации о законе распределения. Для полноты анализа вводятся моменты распределения. Это понятие пришло из механики. Момент определяет эффективность действия силы на придание телу вращательного движения. Статистический момент характеризует силу, приложенную к варианте. Моменты – это обобщающие характеристики, определяющие характер распределения:
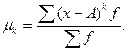
Моментом к-го порядка называют изменения к-тых степеней отклонения признака х от некоторой постоянной А. В зависимости от этой постоянной различают следующие моменты:
1) Начальные,
2) Начальные относительно хо (условные),
3) Центральные.
1) Начальный момент при А=0
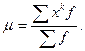
1а) Начальный момент нулевого порядка при к=0
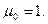
1б) Начальный момент первого порядка при к=1
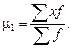
1в) Начальный момент второго порядка при к=2
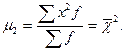
1г) Момент третьего порядка при к=3
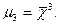
1д) Момент четвёртого порядка при к=4
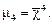
2) Начальный момент относительно хо
при А=хо, где хо – произвольно выбранная величина из ряда распределения.
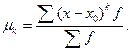
3) Центральный момент при А=х
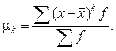
4.Линейный регрессионный анализ.
А) Графический анализ простой линейной регрессии.
Простое линейное уравнение регрессии y=a+bx. Если между случайными величинами У и X существует корреляционная связь, то значение у = ý + e,
где ý – теоретическое значение у, полученное из уравнения ý = f(x),
e – погрешность отклонения теоретического уравнения ý от фактических (экспериментальных) данных.
Уравнение зависимости средней величины ý от х, то есть ý = f(x) называют уравнением регрессии. Регрессионный анализ состоит из четырёх зтапов:
1) постановка задачи и установление причин связи.
2) ограничение объекта исследований, сбор статастической информации.
3) выбор уравнения связи на основе анализа и характера собранных данных.
4) расчёт числовых значений, характеристик корреляционной связи.
Если две переменные связаны таким образом, что изменение одной переменной соответствует систематическому изменению другой переменной, то для оценки и выбора уравнения связи между ними применяют регрессионный анализ в том случае, если эти переменные известны. В отличие от регрессионного анализа, корреляционный анализ применяют для анализа тесноты связи между X и У.
Рассмотрим нахождение прямой при регрессионном анализе: