Средняя арифметическая сгруппированных данных.

Дата: 2025-05-01; Просмотры: 5
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

В таблице приведены данные о размере заработной платы некоторого числа рабочих.

xi f xif
1 2 3
12 10 120
7 35 245
15 5 75
  Σ50 Σ440

 

Формула вычисления: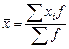

Чтобы найти среднюю арифметическую для дискретного ряда распределения, нужно:

1) Построить граф 3 (xif) и найти произведения варианты на частоту в каждой строке;

2) Подсчитать сумму произведения Σxif;

3) Определить общее число случаев Σf;

4) Найти частное отношение суммы произведений вариантов на частоты к сумме частот.

Полученная величина и будет искомой средней арифметической дискретного ряда распределения сгруппированных данных.

Средняя арифметическая интервального ряда распределения рассчитывается в тех случаях, когда в столбце вариантов не одно, а два значения, показывающие верхнюю и нижнюю границу. Среднее значение интервала находится путём отыскания простой хсер. Между верхней и нижней границами интервала. Число случаев f умножается на эту величину, и находится сумма этих произведений. Формула вычисления в этом случае:

 

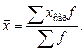
Свойства средней арифметической:

1) Сумма отклонений отдельных вариантов от средней арифметической равна нулю.

2) При умножении или делении всех частот распределения средняя арифметическая остаётся неизменной.

3) Среднее отклонение 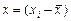, как и полуразмах кварцидей, децилей, редко применяется в хозяйственных расчётах для сравнения степени вариации рядов распределения. При вычислении среднего отклонения суммируются абсолютные значения этих отклонений. А при вычислении среднеквадратического отклонения суммируются квадраты этих отклонений.

 

 

б) Структурные средние.

 

Для характеристики структуры генеральной совокупности используются показатели особого рода, которые называются структурными средними: Мо и Ме.

Мода Мо – это наиболее часто встречающийся признак в вариационном ряду распределения, то есть варианта, которая имеет наибольшую частоту.

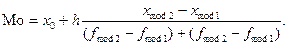
Или в другой форме:

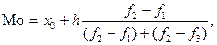
где x0 – нижняя граница модального ряда распределения,

h – шаг распределения,

fмод 2 – частота модального ряда распределения,

fмод 1 – предшествующая частота,

fмод 3 – частота, следующая за частотой модального ряда распределения.

Медиана Ме – это середина упорядоченного ряда распределения, то есть варианта, которая делит, вариационный ряд на две части, равные по числу вариант.

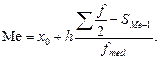
в) Квартили, децили, процентили.

Хотя они и не характеризуют центр рядов рарпределения, они, подобно медиане (она делит ряд распределения пополам), делят ряд распределения:

Квартили – на 4 части,

Децили – на 10 частей,

Процентили – на 100 частей.

 

г) Другие евды средних. Методы их расчета.