Интервальный ряд распределения
| Пример роста детей | Число детей f | В%к итогу | куммулята |
| 1 | 2 | 3 | 4 |
| 90-100 | 5 | 12,5 | 5 |
| 100-110 | 10 | 25 | 15 |
| 110-120 | 20 | 50 | 35 |
| 120-130 | 5 | 12,5 | 40 |
| Итого | 40 | 100% |
Существуют интервальные ряды распределения с неравными промежутками.
Важнейшим требованием к статистическим рядам распределения является
обеспечение сравнения во времени и в пространстве. Вариационные ряды
распределения с равными промежутками обеспечивают это условие, а ряды распределения с неравными промежутками используют для сравнения
плотности распределения. Она определяет количество изучаемых величин в
каждой группе, приходящихся на единицу величины интервала.
Б) Гистограмма, полигон, кривые распределения.
Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.
В случае непрерывного признака целесообразно строить гистограмму, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов и находят для каждого частичного интервала сумму частот вариант, попавших в интервал.
Гистограммой частот называют ступенчатую фигуру, состоящую из
прямоугольников, основаниями которых служат частичные интервалы, а
высоты равны отношению суммы частот вариант к длине интервала
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии, равном плотности частот. Площадь гистограммы частот равна сумме всех частот, т.е. объему выработки.
Полигоном частот называют ломаную, отрезки которой соединяют точки (x1, n1), (х2, n2), и … ,(хk, nk). Для построения полигона частот на оси абсцисс откладывают варианты хi, а на оси ординат - соответствующие им частоты ni,
Точки (хi, ni,) соединяют отрезками прямых и получают полигон частот.
В) Другие методы графического изображения.
Результаты обработки информации выражаются не только в табличной форме, но и в форме графиков и диаграмм, то есть облегчается интерпретация информации ряда распределения.
График - наглядное изображение статистических величин и их соотношений с помощью точек, геометрических фигур и линий в координатной системе.
Диаграмма - графическое изображение, наглядно показывающее соотношение между сравниваемыми величинами.
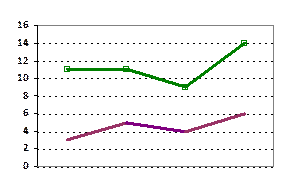
Линейные графики: гистограммы, полигоны, кумулята, связаны с графическим отображением непрерывных данных, сгруппированных в виде ряда распределения таким образом, что по оси У откладываются частоты рядов распределения, а по оси Х- переменные значения (признаки рядов распределения).
Во всех случаях, когда статистические данные поддаются группировке, можно пользоваться диаграммой для упорядочения предварительно собранной информации.
Виды диаграмм:
1) столбиковые;
2) полосовые:
а) с группировкой,
б) составные,
в) простые;
3) линейные;
4) пиктограмма;
5) стратиграмма;
6) круговые:
а) процентные,
б) единичные.
Столбиковые диаграммы строятся следующим образом: по оси X откладываются года, а по оси У - результаты измерения: %, тонны, штуки и т.п. Столбики располагаются вертикально, они не соприкасаются и имеют любую, но одинаковую ширину.
Полосовые:
А) простая - по оси X откладываются значения признака, а по оси У- года.
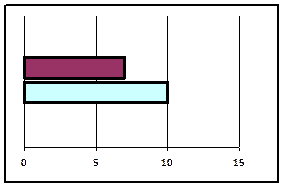
Б) Составные - для представления связанных групп данных на одном графике применяется метод сравнения в кумулятивной форме. Например, выпуск продукции A, В, С. Большое внимание уделяется суммированию групп, часто их представляют разными цветами.
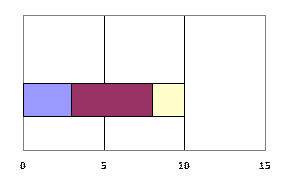
В) с группировкой - используется в том случае, если хотят сравнить группы данных. По оси X располагают значения признака, а по оси У - года.
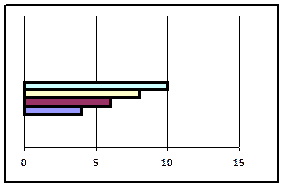
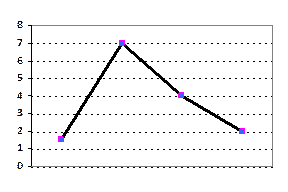
Линейная диаграмма представляет соотношение между временем (по оси X) и частотами по оси У. Соединение точек анаализа даёт кривую, которая соответствует верхней линии стратиграммы.
Пиктограмма - рисованная диаграмма. Она чаще используется в финансовых отчётах и для информирования широкой публики. В ней используется условное изображение.
Стратиграмма - это графическая диаграмма, которая показывает изменение двух или более категорий чисел.
Круговая диаграмма бывает двух типов:
А) процентная - когда, анализируя один год,
за 100% берут круг делят его на части
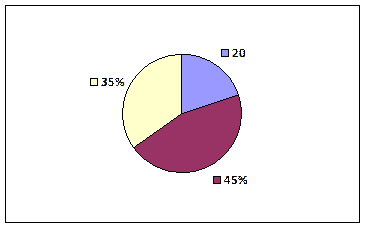
Б) единичная
Все диаграммы, кроме круговых, могут использоваться при изменении данных во времени. Одиночная круговая диаграмма таких изменений не даёт. Только с помощью нескольких круговых диаграмм можно показать изменение признака во времени
|
|
Б) Характеристики центра распределения.
а) Средняя арифметическая.
Пусть изучается генеральная совокупность относительно количественного признака X, и из неё извлечена выборка объемом n..
Выборочной средней арифметической называют среднее арифметическое значение признака выборочной совокупности. Она вычисляется по следующей формуле:
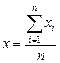, где n – число элементов выборки.
Для средней арифметической генеральной совокупности формула вычисления следующая:
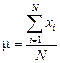, где N – число элементов генеральной совокупности.
При простой средней арифметической частота каждого варианта f = 1.